Устойчивость систем с позиций управления

В нашем восприятии мира представления об устойчиво­сти носят основополагающий характер. Человек может изу­чать и работать с теми объектами, которые ощутимо сохра­няются во времени или повторяются. Без наличия определенной устойчивости не может существовать созна­ние, да и вообще живой организм.

Как вы знаете, любой объект можно рассматривать с точ­ки зрения его внешнего вида, структуры и поведения. Ока­зывается, именно структура объекта в наибольшей степени «отвечает» за его устойчивость. Любой объект можно рас­сматривать как систему, а потому необходимо определить, что же такое устойчивость систем.

Считается, что данная система устойчива, или структур­но устойчива, если при достаточно малых изменениях в ее структуре поведение системы становится в некотором смыс­ле аналогичным поведению исходной системы. Разумеется, в каждом конкретном случае мы должны точно определить, что подразумевается под выражением «достаточно малые» и «аналогично».

Пример. Солнечная система, является устойчивой системой. Эта устойчивость объясняется доминирующим действием Солнца, подавляющим взаимное притяжение планет. Вместе с тем, это действие позволяет планетам двигать­ся. Если бы притяжение было бы очень сильным, плане­ты бы просто бы упали на Солнце.

Предположим теперь, что мы имеем систему притягива­ющихся друг к другу планет без учета притяжения Солнца. В простейшем случае, когда у нас только три планеты, мы приходим к знаменитой и очень сложной задаче «трех тел»: как будет вести себя система из трех тел, между которыми существует сила притяжения, об­ратно пропорциональная квадрату расстояния между ними? Оказывается — очень непросто, и до конца эта за­дача не решена до сих пор.

Пример. Другим астрономическим примером служит внутренняя устойчивость звезды. Она обеспечивается взаимодейст­вием двух противоположных процессов: сжатия вещест­ва под влиянием гравитации и его расширения за счет кинетической энергии, приобретенной в ядерных реак­циях. Сжатие повышает плотность и температуру, что ведет к усилению термоядерной реакции. Полученная при этом кинетическая энергия вещества ведет к расши­рению вещества, а, значит, к понижению температуры и плотности. Тогда уменьшается интенсивность термо­ядерных реакций и гравитационные силы сжимают ве­щество. Устойчивость звезды реализуется в виде слож­ных колебаний.

Пример. Для исследования проблем устойчивости известный спе­циалист по кибернетике У.-Р. Эшби создал модель слож­ной системы — гомеостат, состоящей всего из четырех блоков, связанных между собой определенными связями (рис. 3.5.1). В каждом из них имелся поворачивающий­ся под действием электрического тока магнит, положе­ние которого влияло на величину электрического тока, подаваемого на другие блоки. Когда включали эту систе­му, все магниты начинали поворачиваться под действи­ем токов от других блоков. Эти движения изменяли ве­личину протекающего через магниты тока, который в свою очередь изменял движение магнитов. При этом могло быть два случая: либо после некоторого переходного процесса все электромагниты оказались в некотором устойчивом состоянии и движение прекраща­лось, либо система не находила устойчивого состояния и один из электромагнитов выходил за пределы нормаль­ного отклонения. В схеме в этом случае происходили случайные переключения, и поиски равновесия возоб-

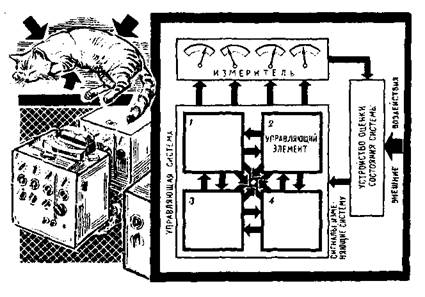
Рис. 3.5.1. Схема гомеостата У.-Р. Эшби

новлялись. В конце концов после нескольких случайных переключений система самостоятельно находила состоя­ние равновесия.

Различные внешние возмущающие воздействия на гоме-остат — перестановки упоров, изменение связей, неболь­шие поломки — не нарушали его способности перехо­дить в устойчивое состояние.

Интересна оценка Н. Винера результатов этих экспери­ментов: «Я полагаю, что блестящая идея Эшби о целе­устремленном механизме, добивающемся своих целей через процесс научения, является не только одним из крупных философских достижений современности, но также ведет к весьма полезным техническим выводам в решении задач автоматизации. Мы не только можем придавать целевую направленность машине, но в подав­ляющем большинстве случаев машина, сконструирован­ная для того, чтобы избегать аварийных ситуаций, будет отыскиввать цели, которые она может осуществить».

При изучении устойчивости динамических систем очень важным является понятие аттрактора (to attract — притя­гивать), т. е. такого состояния динамической системы, к ко­торому она стремится, «притягивается». Это состояние мо­жет быть описано множеством, которое также называют аттрактором.

Пример. Простым примером динамической системы, иллюстри­рующей понятие аттрактора, является маятник. Обыч­ный движущийся маятник под действием сил трения в конце концов останавливается в точке, которая и есть в данном случае аттрактор, поскольку именно эта точка в процессе движения «притянула к себе» маятник. Если описать движение маятника в прямоугольной сис­теме координат, где по одной оси откладывается угол от­клонения маятника от вертикали, а по другой — ско­рость изменения этого угла (в математике это называется фазовой плоскостью), то получим постепен­ное приближение маятника к аттрактору — началу ко­ординат (рис. 3.5.2).

Рис. 3.5.2

Движение обычного маятника

-г

::>°л. ■■->■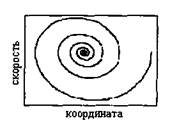

Пример. По другому ведет себя динамическая система, состоящая из часового механизма, маятника и груза на цепочке. Если раскачать маятник сильным толчком, то он начнет сильно раскачиваться, замедляясь затем до некоторого стабильного режима колебаний. На фазовой кривой этот режим изображается окружностью, которая в данном случае и является аттрактором (рис. 3.5.3).

Рис. 3.5.3

Движение маятника часов

Управляющие воздействия должны, с одной стороны, обеспечивать достижение поставленной цели, с другой — не нарушать относительной устойчивости системы, если система является изначально устойчивой. Если же напротив, система изначально является неустойчивой (например, государство в момент кризиса), то управление с необходимостью должно привести систему к относительно устойчивому состоянию.

И системы, управляемые субъектом, и самоуправляющие­ся системы могут быть устойчивыми или неустойчивыми.

Устойчивость системы управления может быть достигну­та разными очень разными путями, иногда очень простыми и остроумными.

Пример. Известно, что на военном флоте с давних времен устные команды и распоряжения, дословно повторяются теми, к кому они относятся. Например, офицер командует: «поднять якорь», а матрос отвечает «есть поднять якорь». Этим простым приемом достигается значитель­ная надёжность в управлении сложной системой — ко­раблем. При шуме ветра и волн матрос мог неправильно понять приказ, и его дублирование позволяло офицеру это проконтролировать.

По-видимому, самым эффективным средством повыше­ния устойчивости управляемых и самоуправляющихся сис­тем — это усиление влияния субъекта управления.

Пример. Как известно, в 1929 году в США и многих странах Запад­ной Европы разразился глубочайший экономический кри­зис, получивший название Великой депрессии. Решающая роль в его преодолении принадлежала государству (субъ­екту управления). Например, военные расходы правитель­ства США в 1941 году увеличились на 105% (по сравне­нию с 1940 г.), в 1942 году - на 175%, а в 1943 году еще на 50%. В 1944 году расходы правительства США даже с поправкой на рост цен были в 6,5 раза выше, чем в 1940 году. Именно военные расходы встряхнули экономику США и вывели ее из трясины Великой депрессии.

Если цели управления и управляющие воздействия субъ­екта управления хорошо согласованы, состояния неустойчи­вости системы практически не возникают, поскольку субъ­ект, как правило, с помощью обратных связей оперативно реагирует на первые признаки неустойчивости и стабилизи­рует систему. Иное дело самоуправляющаяся система или система, в которой субъект управления фактически не вы­полняет своих управленческих функций. В таких системах часто возникают кризисные ситуации. С точки зрения тра­диционной схемы управления эти состояния крайне нежела­тельны. Но существует и такая точка зрения, что в кризисах заложен эффективный инструмент управления.

Фундаментальной значение в этом случае приобретают так называемые точки бифуркации (от французского bifurcation — раздвоение), то есть такие точки, в которых система стано­вится неустойчивой и ее дальнейшее развитие возможно в разных направлениях в зависимости от случайных факторов.

Пример. Пусть к балке, изображенной на рисунке 3.5.4. прило­жена переменная сила F. Какое-то время балка нахо­дится в устойчивом состоянии, а затем, при некотором значении F₀ прогибается. При этом, в какую сторону она прогнется — вправо или влево — зависит от случай­ных факторов. Значение силы F₀ и определяет точку би­фуркации. Возможное развитие системы показано на графике.

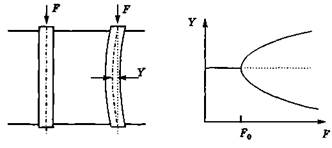
Рис. 3.5.4. Прогибание балки под воздействием силы

Как свойство точек бифуркации используется в процессе управления? Предположим, что существует субъект, кото­рый поставил перед собой цель прогнуть балку в определен­ную сторону.

Будем считать, что балка является достаточно прочной и прямое управляющее воздействие, необходимое для изгиба­ния балки является очень большим и, возможно, недости­жимым для субъекта.

Однако, зная свойства точек бифуркации, можно карди­нально поменять стратегию управления. Можно, используя тот факт, что на балку действует сила F, в точке бифурка­ции F_Q, подействовать на нее малой силой и добиться желае­мого результата.

Пример. Управление с использованием так называемых малых резонансных воздействий в точках бифуркации известно очень давно. Как свидетельствует история, рядом с вла­стным лицом, не отличающимся умом или сдержанно­стью, всегда находится некто, кто в критические момен­ты (то есть точки бифуркации) дает ему советы, направляя его волю в определенную сторону. История сохранила для нас имена многих таких людей: шут Шико при французском короле Карле IX (по версии А. Дюма), Э. И. Бирон при русской императрице Анне Иоанновне, философ Сенека при римском императоре Нероне и др.

Управление через малые резонансные воздействия в неу­стойчивых ситуациях может быть более эффективным, чем директивное (авторитарное) и демократическое (коллектив­ное) управление. В социальных системах тому немало под­тверждений. Возможно, поиски возможности реализации такого рода управления в технических системах приведут к интересным открытиям.

Система называется структурно устойчивой, если при до­статочно малых изменениях в ее структуре поведение систе­мы становится в некотором смысле аналогичным поведению исходной системы.

При изучении устойчивости динамической системы очень важным является понятие аттрактора — такого состояния системы, к которому она стремится, «притягивается». Это состояние может быть описано множеством, которое также называют аттрактором.

Понятие аттрактора является обобщением понятия рав­новесия.

Фундаментальное значение в изучении поведения систе­мы и ее устойчивости имеют точки бифуркации, то есть та­кие точки, в которых система становится неустойчивой и направление ее дальнейшего развития зависит от случайных факторов.

Задание 1

Приведите примеры устойчивых и неустойчивых систем, извест­ных вам из курсов физики, химии, биологии.

Задание 2

Определите, какие факторы (внутренние и внешние) могут вли­ять на устойчивость системы. Может ли управление быть одним из таких факторов?

Задание 3

Разработайте схему управления транспортным потоком после выпадения обильных снегопадов, приводящую транспортную систему к стабильному работоспособному состоянию.

Задание 4

Определите, являются ли следующие системы устойчивыми:

а) метроном;

б) экосистема в пруду для разведения рыбы;

в) стая обезьян;

г) система управления железнодорожным транспортом;

д) система образования.

(Cffi вопрос-проблема

1. Как следует из доклада ООН о развитии человечества
за 1998 год, три самых богатых человека в мире имеют сово­
купное личное состояние, превышающее валовой продукт
48 наименее развитых стран, 225 самых богатых людей пла­
неты имеют совокупное состояние более чем 1 трл долларов,
а 3/5 из 4,4 млрд жителей развивающихся стран лишены
канализации, 1/3 — чистой воды, 1/5 — медицинского об­
служивания. Американцы тратят на косметику 8 млрд дол­
ларов в год. По оценкам ООН, 6 млрд. долларов хвалило бы
для того, чтобы дать всем детям мира начальное образова­
ние. Европейцы съедают мороженого на 11 млрд долларов в
год, хотя 9 млрд долларов хватило бы на то, чтобы обеспе­
чить чистой водой и надежной канализацией всех нуждаю­
щихся в мире. Американцы и европейцы тратят 17 млрд
долларов на корм для домашних животных, но 13 млрд хва­
тило бы, чтобы обеспечить элементарную медицинскую по­
мощь всех нуждающихся по всему миру.

Можно ли такую цивилизацию считать устойчивой систе­мой? Каковы возможные перспективы её развития?

2. Чем, по вашему, является массовая культура — искус­
ством или инструментом управления?

Как показали исследования американского экономиста Д. Стиглера (Нобелевская премия по экономике 1982 года), в самоуправляемых системах большинство прогнозов оказы­ваются неточными, а решения принимаемые на их основе — неэффективными. Например, ни одно из постановлений пра­вительства США, которое в течении ряда лет пыталась регу­лировать экономику, не дало ожидаемых результатов. Более того, эти результаты были прямо противоположными тем, которые ожидали. Причина была в том, что в условиях неу­стойчивого развития системы схема: «управляющее воздей­ствие — желаемый результат» не работает. Управление ста­новится эффективным в том случае, когда главное не сила, а правильная организация воздействия на систему. Слабые, но правильно организованные, соответствующие структуре и тенденциям ее развития воздействия, оказывают более за­метное влияние на систему, чем сильные, но прямые управ­ляющие воздействия. Такие воздействия получили название «слабых резонансных воздействий». Характерно, что наблю­датель, находящейся «внутри» системы, слабые резонанс­ные воздействия практически не замечает, даже если они имеют искусственный характер.

Рассмотрим простейшую модель кругооборота капитала в какой-нибудь банковской системе.

Пусть в эту систему входит три банка: А, В, С, которые продают и покупают акции. Чтобы избежать больших чи­сел, будем считать, что стоимость всех акций ограничена единицей.

Предположим следующее:

• банк А продает некоторые акции по цене X.

• банк В, купив эти акции, в силу сложившихся обстоя­тельств вынужден продавать их по цене 1-Х.

• банк С, покупая акции у банков А и В, продает их по цене Х(1-Х).

• банк А, реагируя на такое изменение цены акций сам на­чинает продавать их по цене Х(1-Х), умноженной на не­который коэффициент к, то есть по цене кХ(1-Х).

Рис. 3.5.5. Схема кругооборота капитала в условной банковской системе

При фиксированном коэффициенте к мы имеем систему, поведение которой зависит от значения к. Таким образом, к можно рассматривать как управляющее воздействие на дан­ную систему.

Данная модель может быть реализована на компьютере. Тогда зависимость поведения системы от значения к можно детально исследовать с помощью компьютерного экспери­мента (подробно об этом см. параграф главы 4, посвящен­ный компьютерному эксперименту).

В итоге получается следующая картина.

При к < 3 переменная X стремиться к некоторому фикси­рованному значению Х₀. В этом случае, аттрактор данной системы состоит из одной точки. Это — стабильное состоя­ние системы.

При малом увеличении к (немного больше 3) значение X начинает колебаться между двумя значениями. Аттрактор системы теперь уже состоит из двух точек Х₀ и X,. Эта со­стояние системы уже не стабильно, хотя его еще можно счи­тать устойчивым. При этом, некоторое значение к₀ опреде­ляет точку бифуркации: систему в точке к₀ можно привести к стабильному состоянию со значением Х₀ и X, с помощью малого дополнительного воздействия.

При увеличении к свыше к₀ количество точек аттрактора возрастает и система, соответственно, становится менее и менее устойчивой.

Наконец, при к больших некоторого значения Ц перемен­ная X начинает принимать бесконечное число значений. Си­стема полностью теряет устойчивость. Образуется хаос.

Анализ приведенного примера подсказывает две основ­ные стратегии управления.

1. Управляя только параметром к, добиться стабильного состояния системы. В этом случае можно ориентироваться на традиционную схему управления, приведенную в §1 дан­ной главы. Субъектом управления, в этом случае выступает банк А, а целью управления — создание стабильной банков­ской системы.

2. Попытаться повысить свои доходы, используя нестаби­льность системы. Для этого необходимо зафиксировать зна­чение к₀ параметра к. Система перейдет в самоуправляемое состояние с двумя возможными значениями параметра X: Х₀ и Х_г Путем малого постороннего воздействия необходи­мо «подтолкнуть» систему к «выбору» нужного значения X. После этого можно объявить X результатом «правильно ор­ганизованного» самоуправления. Далее можно попытаться улучшить результат и перейти к точке бифуркации k_r По­следствия этого шага определяется известной пословицей: «либо пан, либо пропал», поскольку в случае ошибки управ­ления система превращается в хаос.

Данный пример показывает, какую роль в управлении играют точки бифуркации. Эти точки можно выявлять, что­бы избежать их и сохранить систему в стабильном состоя­нии, но можно создавать специально, исходя из опеделен-ных целей управления. Более того, в любой реальной системе речь идет не об отдельной ситуации неустойчивости, а о целом каскаде бифуркаций.

Управление через нестабильное состояние системы с не­обходимостью подразумевает наличие, как минимум, двух взаимосвязанных управляющих воздействий:

• воздействие, создающее каскад бифуркаций;

• слабое целенаправленное (резонансное) воздействие в точ­ках бифуркаций.

В общем виде, схема управления системой через ее неста­бильность выглядит так, как показано на рис. 3.5.6.

Воздействие, создающее каскад бифуркаций направлено, как правило, на разрыв системных связей между управляв-

Рис. 3.5.6. Схема создания ситуаций нестабильности в самоуправляющейся системе

мым объектом и другими объектами системы. Потеряв или существенно ослабив системные связи, объект становится «подвижным» и очень чувствительным даже к слабым управляющим воздействиям.

Как известно, системные связи могут иметь материаль­ный или информационный характер. В последнем случае речь идет об общности информационных моделей, которыми руководствуются объекты системы в своей деятельности. Дестабилизирующее воздействие направлено, как правило, на разрушение именно этих, информационных связей, то есть на деформацию всей информационной системы.

В неустойчивом состоянии слабое воздействие на систему может быть абсолютно незаметно для объекта управления. В этом случае он оказывается похожим на падающий камень, который по выражению философа Б. Спинозы (1632-77) ду­мает, что он падает по своей воле. Это значит, что управляю­щее воздействие, равно как и его цель оказываются для объ­екта управления, во многом, анонимными.

Глава 4