Разнообразные массовые явления, изучаемые статистикой, можно подразделить на два вида: простые и сложные.
В одних совокупностях входящие в них единицы поддаются суммированию (объем выпускаемой продукции одного вида, размер посевных площадей, численность работающих и т.п.). Поэтому изменение объема изучаемой совокупности во времени и пространстве достигается сопоставлением количества единиц в отчетном и базовом периодах, по различным территориям между собой. Показатели, характеризующие такие совокупности, выражаются абсолютными величинами, т.е. являются объемными. Такие совокупности называются простыми. Статистические показатели, характеризующие эти совокупности – это объемы (суммы) изучаемых признаков или средние их значения.
В то же время имеются и такие совокупности, по которым показатели нельзя суммировать (например, себестоимость продукции по предприятиям, производительность труда и заработная плата работающих и т.п.). Эти показатели условно называют качественными. Они обычно выражаются в виде средних величин. В статистике такие явления или совокупности называются сложными. Обобщенную характеристику изменения объема (размеров) явления в пространстве и времени в этом случае приходится давать при помощи специально построенных показателей – индексов.
Слово «индекс» в переводе с латинского (index) означает «указатель», «показатель». Как видели выше, этот статистический показатель используется для целей сопоставительного анализа развития явления во времени, т.е. является относительной величиной.
Итак, статистический индекс – это относительная величина сравнения сложных совокупностей и отдельных их частей.
Следует иметь в виду, что не всякая относительная величина является индексом. Например, относительные величины структуры, интенсивности к индексам не относятся.
Индексы как сводные статистические показатели исчисляются с учетом специальных принципов и методов, которые в статистике объединяются понятием теории индексного метода.
Прежде всего, индекс – это относительный показатель, получающийся в результате сравнения двух величин, характеризующих уровень изучаемого явления для двух разных периодов.
В теории индексов тот показатель, изменение которого характеризует индекс, называется индексируемой величиной. Величина, которую сравнивают и которая стоит в числителе индексного отношения, характеризует уровень для отчетного периода: чтобы различать отчетный период принято возле символа индексируемой величины внизу ставить знак «1». Величина, с которой сравнивают и которая стоит в знаменателе индексного отношения, характеризует уровень для базисного периода (обозначается внизу символа индексируемого показателя знаком «0»).
Индекс как относительный показатель может быть выражен в виде коэффициентов (когда базовый уровень принят за 1) или в виде процентов (когда он принят за 100). Если индекс больше 1 (или 100%) уровень изучаемого явления растет, если меньше 1 (или 100%) – снижается.
Расчеты многих индексов сложны, методология этих расчетов составляет предмет теории индексного метода (основные положения будут рассмотрены ниже).
Индексный метод в статистических исследованиях применяется очень широко. Можно выделить три основные сферы применения индексного метода:
- сравнительная характеристика сложных совокупностей (индексы роста и прироста, индексы выполнения плана, территориальные индексы);
- анализ динамики средних показателей: зависящих от изменения структуры совокупности;
- изучение связей и оценка доли отдельных факторов в изменении сложного явления.
Индексы классифицируются по ряду признаков:
1)В зависимости от характера объектов исследования различают индексы объемных и индексы качественных показателей.
К первой группе относятся индексы физического объема продукции, национального дохода, розничного товарооборота, потребления и т.д. Они исчисляются на основе величин объемных показателей.
Ко второй группе относятся индексы себестоимости продукции, производительности труда, цен и т.д. Они исчисляются на основе качественных показателей.
Для обеспечения сопоставимости составных частей индексируемых величин в расчет вводится показатель соизмерения, вес, позволяющий обеспечить количественную сравнимость за отчетный и базовый периоды. Например, при расчете индекса физического объема продукции количества производимых видов продукции оцениваются по одинаковым ценам. При расчете индекса себестоимости осуществляется охват одинакового количества продукции.
2) По степени охвата элементов (единиц) совокупности индексы делятся на индивидуальные, групповые и общие.
Индивидуальные индексы дают сравнительную характеристику отдельных элементов той или иной совокупности. Например, индекс производства отдельной продукции, цены конкретного товара.
Групповые индексы охватывают часть (какую-то группу) единиц совокупности. Иногда их называют субиндексами. Например, индексы объема производства продукции по отдельным отраслям промышленности.
Общие индексы характеризуют изменение совокупности в целом. По своему содержанию являются сводными относительными показателями. Они выражают среднее изменение, например, объема продукции промышленности, цен, заработной платы.
Групповые индексы позволяют изучить закономерности в изменении структуры, в развитии отдельных частей изучаемого явления. В них находит выражение непосредственная связь индексов с методом группировок.
Важной особенностью общих индексов является то, что они обладают синтетическими и аналитическими свойствами.
Синтетические свойства индексов состоят в том, что посредством индексного метода производится соединение (агретрование) в целое разнородных единиц статистической совокупности.
Аналитические свойства индексов состоят в том, что посредством индексного метода может определяться влияние отдельных факторов на изменение изучаемого явления, влияние структурных сдвигов.
3) В зависимости от методологии расчета общие и групповые индексы подразделяются на агрегатные (суммарные) и средние из индивидуальных индексов.
Агрегатная форма индексов является основной формой расчета общих индексов. Для расчета агрегатных индексов используются так называемые соизмерители (веса) индекса, которые позволяют преодолеть несоизмеримость отдельных элементов и суммировать разноименные индексируемые величины.
Средний взвешенный из индивидуальных индексов позволяет получить тот же результат, что и агрегатный индекс.
В теории статистики при выборе весов пользуются следующими правилами: индексы динамики количественных (объемных) показателей рассчитывают с весами базового периода, а качественных – с весами текущего периода. Такое правило сообразуется с сущностью рассчитываемых показателей, и, кроме того, позволяет построить систему взаимосвязанных индексов.
4) В зависимости от задач исследования (или выбора периода анализа) могут быть рассмотрены отдельный индекс или ряд индексов.
Отдельный индекс рассчитывается только по двум: отчетному (текущему) и базовому периодам.
Ряд индексов исчисляется за несколько периодов. При этом веса в этом ряду могут быть постоянными, т.е. относящимися у всех индексов к одному периоду, или переменными, т.е. изменяющимися от индекса к индексу. В первом случае говорят о системе (ряде) базисных индексов, а во втором случае получают систему цепных индексов.
Индивидуальные индексы принято обозначать символом «i», а общие индексы - J.
Индивидуальные индексы
В зависимости от степени охвата подвергнутых обобщению единиц изучаемой совокупности, как отмечалось в 1-м вопросе, индексы подразделяются на индивидуальные (элементарные) и общие.
Индивидуальные индексы характеризуют изменения отдельных единиц (элементов) статистической совокупности.
Для определения индекса надо произвести сопоставление не менее двух величин, отражающих изменения индексируемого показателя (признака). Например, при изучении изменения физического объема продукции в качестве индексируемой величины выступают данные об объеме (количестве) продукции в натуральных измерениях; при изучении изменения цен индексируемой величиной является цена единицы товара и т.д.
Как отмечалось выше, индекс – это относительный показатель, получающийся в результате сравнения двух величин, характеризующих уровень изучаемого явления (единицы совокупности) для двух разных периодов (в динамических индексах) или разноименных показателей качественно однородного сложного явления за определенные периоды времени (в индексах сложного явления).
Индивидуальные индексы физического объема продукции (реализации товаров, товарооборота и т.д.) определяются по формуле
,
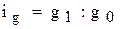где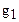 
и 
- соответственно количество (объем) производства продукции (продажи) отдельных видов в текущем (отчетном) и базисном периодах в натуральных измерителях.
Для определения индивидуальных индексов цен применяется формула
,
где 
и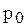 
- цены за единицу продукции (товара) определенного вида в текущем и базисном периодах.
Результат расчета индексных отношений может выражаться в коэффициентах или в процентах. При этом, как уже говорилось выше, если индекс больше 1 (или 100%) уровень изучаемого признака (явления) растет, если меньше 1 (или 100%) – снижается.
Как видим, индивидуальный индекс очень прост в своем расчете и здесь никаких методологических трудностей не возникает.
А) Однако, и при расчете индивидуального индекса необходимо учитывать сущность рассматриваемого признака (показателя, явления). Например, уровень производительности труда может оцениваться с использованием двух взаимосвязанных показателей – выработки (объема произведенной продукции в единицу времени) или трудоемко (затратами труда на производство одной единицы продукции). Между этими показателями существует обратная зависимость. Повышение производительности труда выражается или увеличением выработки (В) или снижением трудоемкости.(t) Отсюда индивидуальный индекс производительности труда определяется как:
или 
.
В первом случае используется известное индексное выражение, а во втором случае индивидуальный индекс производительности труда определяется как уровень трудоемкости базисного периода и уровню трудоемкости отчетного периода.
Б) Рассмотрим пример. Имеются следующие данные о ценах продукта «К»:
Сентябрь 
| Ноябрь 
| Индивидуальный индекс цен ( )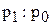
| |
| Модальная цена рынка за 1 кг., тыс.руб. | 1, 33 или 133 % | ||
| Договорная цена за 1 кг., тыс.руб. (по розничной торговле) | 1, 00 или 100% |
При анализе цен возможна такая постановка: определить соотношение цен розничной торговли и рынка.
В этом случае, например, индекс ноября исчисляется так:
или 
Первый индивидуальный индекс показывает, что цена 1 кг продукта «К» на рынке была в ноябре в 2 раза выше договорных цен розничной торговли. А второй индекс показывает, что договорная цена в ноябре была на 50% ниже уровня цены рынка 
.
Аналогично можно сопоставить уровни разноименных показателей за один и тот же период, переставив их местами.
Из рассмотренного примера видно, что при вычислении индивидуальных индексов база сравнения имеет определяющее значение на величину индекса, а выбор базы сравнения определяется целью исследования.
В) Другой особенностью индивидуальных индексов является то, что они характеризуют изменение во времени (или соотношения в изменении) единичных простых показателей.
Однако в области экономических явлений гораздо чаще приходится при помощи индексов характеризовать изменения сводных показателей, сложных явлений. Строго говоря, такого рода сводные относительные показатели, характеризующие изменение сложного явления в целом, представляют собой собственно индексы, к построению которых и относится теория индексов.
Общие индексы характеризуют изменение совокупности в целом. Общие индексы могут исчисляться как по агрегатной форме, так и в форме взвешенной средней из индивидуальных индексов. Выбор формы общих индексов зависит от характера исходных данных.
