Важным направлением в исследовании массовых явлений и процессов выступает изучение основной или общей тенденции их развития (тренда).
Как уже неоднократно подчеркивалось в предыдущих частях, многочисленные факторы, под действием которых формируются и изменяются уровни рядов динамики изучаемых явлений, неоднократны по силе, направлению и времени их действия
Поставленные действующие факторы оказывают на изучаемые явления определяющее влияние и формируют в рядах динамики основную тенденцию развития (тренд). Воздействие других факторов проявляется периодически и вызывает повторяемые во времени колебания уровней рядов динамики (так называемые сезонные колебания). Действия разовых (спорадических) факторов отображаются случайными (кратковременными) изменениями уровней рядов динамики. Исходя из этого при анализе рядов динамики необходимо изучить основные компоненты рядов: тренд, периодически (сезонные) колебания, случайные отклонения.
Как показывает практика, в одних рядах основная тенденция развития проявляется достаточно четко на основе анализа статических показателей направления и интенсивности развития (тестов роста, прироста, изменения уровней, средних величин), в других ряда она может быть выявлена с использованием специальных методов анализа рядов динамики. Выбор конкретных методов статистики для этой цели зависит от характера исходной информации и предопределяется задачами анализа.
Рассмотрим основные методы преобразования рядов динамики, позволяющие обнаружить и обосновать основную тенденцию в развитии явления. На практике наиболее распространенными методами статического изучения тренда являются: укрупнения интервала, сглаживание скользящей средней, аналитическое выравнивание.
Метод укрупнения интервалов является наиболее простым методом преобразования ряда с колеблющимися уровнями с цепью выявления тренда. Главное в этом методе заключается в преобразовании первоначального ряда динамики в ряды более продолжительных периодов (например, месячные в квартальные, квартальные в годовые и т.д.) Уровнями ряда с укрупненными периодами могут быть средние величины первоначальных уровней по новым периодам. Недостаток метода: резко сокращается количество уровней.
Так, ряд урожайности по годам обнаруживает колебания, обусловленные метеорологическими условиями отдельных лет. Переход к ряду средних по пятилетиям продолжительным периодам позволяет более ясно видеть общую тенденцию в изменении урожайности во времени.
Довольно часто при обработке динамического ряда с целью определения тенденции развитии массового явления применяется сглаживание методом скользящей средней (называемый также методом подвижной средней).
Суть этого метода заключается в замене фактических уровней первоначального ряда новым рядом подвижных (скользящих) средних, которые рассчитываются для определенных последовательных подвижных (скользящих) интервалов, т.е. по определенному числу членов первоначального ряда. Причем при вычислении каждой новой средней отбрасывается один член ряда слева и присоединяется один член справа.
Первоначальный ряд можно сглаживать средними за два, три, четыре, пять и т.д. интервалов (периодов) первоначального ряда. Чем меньше интервала сглаживания, тем более сглажены ряд ближе к первоначальному ряду фактических уровней. Чем больше интервал, за который исчисляется средняя, тем более сглаженной ряд осередняет фактические уровни первоначального ряда.
Для сглаживания ряда динамики способом скользящей средней, например, из 5 членов, необходимо последовательно по изложенной выше методике суммировать по 5 членов и результаты делить на 5.
Недостатком данного метода сглаживания ряда является то, что сглаженный ряд оказывается короче первоначального на (n-1)\2 члена с одного и другого конца (под «n» имеются в виду числа членов или периодов, из которых рассчитывается скользящие средние).
На практике обычно выравнивание осуществляется с нечетным числом членов или периодов первоначального ряда. В этом случае вычисляемые средние относятся к середине подвижного интервала сглаживания. При сглаживании его четному числу членов средняя приходится между двумя временными точками (периодами). Чтобы такие средние привязать к определенней временной точке используется специальный прием, называемый центрированием. Суть его в том, что из каждой пары сглаженных скользящих средних рассчитывается средняя арифметическая, которая и относится к определенной временной точке (или определенному периоду).
Следует иметь ввиду, что слишком укороченный ряд скользящих средних может оказаться недостаточно репрезентативным (убедительным) для характеристик тенденции исследуемого ряда динамики.
Применение в анализе рядов динамики методом укрупнения интервалов и скользящей средней позволяет выявить тренд для его описания, но получить обобщенную тенденцию количественную статическую оценку тренда посредством этих методов невозможно. Решение этой более высокого порядка задачи – измерение тренда – достигается методом аналитического выравнивания.
При этом способе каждый фактический уровень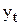 
рассматривается как сумма двух слагаемых
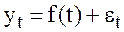
где f(t) – систематическая составляющая, отражающая тренд и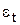 
– случайная составляющая величина.
Задача выравнивания ряда сводится к определению адекватного тренду вида математической функции, отысканию на основе фактических данных параметров функции и переходу к ряду с расчетными («теоретическими») уровнями по найденной формуле (виду) функции.
Если выбранный тип (вид) математической функции f(t) адекватен основной тенденции развития изучаемого явления во времени, что тем самым будет определено количественное измерение тренда.
Одним из условий обосновано применения метода аналитического выравнивания является знание эталонных типов развития и сущности изучаемых массовых явлений.
Различают несколько эталонных (основных) типов развития массовых явлений во времени:
1) равномерное развитие. Для этого типа динамики присущи устойчивые постоянные абсолютные ценные приросты
.
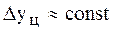Основная тенденция (тренд) в таких рядах обращается уравнением прямолинейной функции
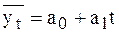
где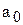 
и 
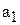– параметры уравнения; t – время.
Параметр 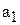определяет направление развития. Если 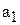>0, то уровни ряда динамики равномерно возрастают, а при 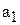<0 происходит их равномерное снижение;
2) равноускоренное (равнозамедленное) развитие.
Уровни таких типов рядов динамики изменяются с постоянными темпами роста
.
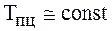Основная тенденция развития в рядах динамики в этом случае в этом случае отображается функции параболы 2-го порядка
.
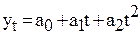Значения параметров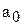 
и 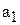идентичны параметром прямой, а параметр 
характеризует постоянное изменение интенсивности развития (в единицу времени). При >0 происходит ускорение развития, а при <0 идет процесс замедления роста;
3) развитие с переменным ускорением (замедлением). Для этого типа динамики основная тенденция развития выражается функцией параболы 3-го порядка
.
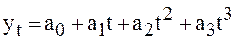Параметр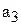 
отображает изменение ускорения. При 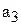>0 ускорение возрастает, а при 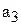<0 ускорение замедляется;
4) развитие по экспоненте. Этот тип динамики характеризуют стабильные темпы роста
.
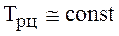Основная тенденция в рядах динамики в этом случае отображается показательной функцией
.
где 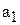– темп роста (снижения) изучаемого явления в единицу времени, т.е. интенсивности развития.
5) развитие с замедлением в конце периода. У этого типа динамики ценные абсолютные приросты сокращаются в конечных уровнях ряда динамики
.
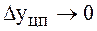Основная тенденция развития в таких рядах динамики выражается следующей логарифмической функцией
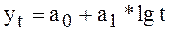
При аналитическом выравнивании в рядах динамики можно применить и другие математические функции. Так, при изучении основной тенденции неудовлетворенного и реализованного спроса населения применяются
степенная функция: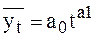 
;
функция гиперболы: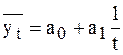 
.
Специфика и основные свойства математических функций рассматриваются в курсах "Экономико-математические методы» и «Математическая статистика».
Практика статического изучения тренда массовых явлений показывает, что зачастую невозможно однозначно решить вопрос, какому типу развития больше всего отвечают показатели ряда динамики. Ведь рассмотренные выше признаки классификации типов развития (абсолютные приросты, темпы роста и прироста) весьма схематичны. В лучшем случае на основе качественного анализа ряда динамика может быть выдвинута рабочая гипотеза о возможных типах развития. Но выбор на этой основе конкретной математической функции весьма затруднителен. Однако возможности широкого использования в анализе трена современных ЭВМ позволяет успешно решать проблему выбора адекватной модели тренда. Обычно из качественно анализа рядов динамики намечаются типы функций, которые могут отобразить имеющиеся в изучаемом ряду изменения во времени. Затем определяются изменения тренда исходных данных по намеченным математическим функциям. В заключение по результата сравнительного анализа полученных решений с учетом существа изучаемого явления выбирается наиболее адекватное тренду решение.
В качестве примера аналитического выравнивания рассмотрим методику выравнивания ряда динамики по прямой линии.
Уравнение прямой линии может быть выражено, как видели выше, следующей формулой
.
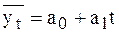Задача сводится к тому, чтобы фактические уровни ряда динамики (у) заменить расчетными («теоретическими») уровнями (
), исчисленными на основании этого уравнения.
Вычисленная прямая, выравнивающая первоначальный ряд, должна проходить в максимальной близости к фактическим уровням ряда. Следовательно, определить 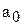и 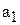такими, чтобы разности между 
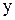и , вычисленных по этим значениям 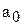и 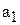, были минимальными. Эта задача может решаться с использованием различных методов. Как правило, для этой цели применяют известный в математике способ (метод) наименьших квадратов
.
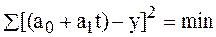Рассматривая эту сумму как функцию 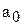и 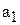, дифференцируем ее по этим параметрам и приравниваем производные нулю
.
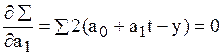
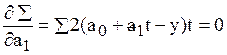Отсюда с помощью простых преобразований для нахождения параметров 
и 
искомой прямой линии получаем систему двух нормальных уравнений
,
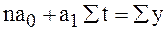
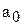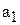где y – уровни фактического ряда динамики, n – число членов ряда, t – показатели времени (дни, месяцы, годы и т.д.), и - параметры прямой.
С использованием ЭВМ решение этой системы нормальных уравнений осуществляется на базе стандартных программ.
Для решения данной системы уравнений можно воспользоваться способом определителей. Откуда
; 
.
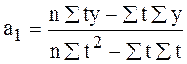Эта система может решаться и упрощенным способом: исходя из того, что в рядах динамики значения t являются показателями времени, то всегда им можно придать такое значение, чтобы их сумма была равна нулю, т.е.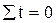 
. В этом случае система нормальных уравнений принимает вид
;
.
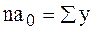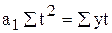Откуда имеем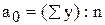 
и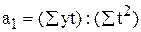 
.
При нечетном числе уровней ряда (при равных интервалах) серединная точка (год, месяц…) принимается за 0. Тогда предшествующие периоды обозначаются соответственно через -1, -2, -3 и т.д., а последующие за средним периоды соответственно +1, +2, +3 и т.д.
При четном числе уровней ряда два серединных момента времени принимаются за -1 и +1, а величина интервала времени принимается за 2: выше срединных моментов времени имеем -3, -5 и т.д., а ниже соответственно 3, 5, 7 и т.д.
Обычно примеры выравнивания рядов динамики по другим функциям приводятся в учебниках по курсу общей теории статистики.
В условиях всеобщей компьютеризации общества аналитическое выравнивание выполняется на ЭВМ с использованием пакета стандартных (прикладных) программ.
