При расчете отдельно взятого индекса веса в числителе и знаменателе относятся к одному и тому же периоду, т.е. всегда одинаковы.
Пусть, например, за ряд периодов имеются данные о каком-то единичном показателе:
| Периоды | I | II | III | IV | V |
| Уровни | y1 | y2 | y3 | y4 | y5 |
В этом случае, веса в вычисляемых индексах могут быть как постоянными (т.е. у всех индексов относящихся к одному периоду), так и переменными (т.е. изменяющиеся от периода к периоду).
Примем за базу сравнения y1, тогда для периодов II, III, IV, V индексы последовательно будут выражены (с постоянной базой) следующим образом:
 .
.
Полученный ряд индексов называется базисными индексами (или коэффициентами роста с постоянной базой).
Теперь будем исчислять ряд индексов как отношение двух соседних уровней. Тогда для периодов II, III, IV, V индексы последовательно будут выражены (с переменной базой) следующим образом:
 .
.
Полученный ряд индексов называется цепными индексами.
Нетрудно заметить, что

Цепные и базисные индексы с постоянными весами – соизмерителями находятся в следующей взаимосвязи:
1) произведение цепных индексов дает базисный индекс (последнего периода)
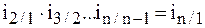 ;
;
2) деление последующего базисного индекса на предыдущий базисный индекс дает цепной индекс (последующего периода), т.е.
 .
.
Отмечая эту взаимосвязь между цепными и базисными индексами следует иметь в виду, что она должна использоваться с определенными оговорками: для индивидуальных индексов эта взаимосвязь выполняется всегда (безусловно), а для общих индексов будет иметь место только тогда, когда ряд общих индексов рассчитан по одним и тем же весам (т.е. для так называемых индексов с постоянными весами).
Как видели в п. 10.3 настоящей темы, все индексы объемных (количественных) показателей исчисляются по весам – соизмерителям базисного периода, т.е. с постоянными весами. Поэтому к таким индексным рядам указанная взаимосвязь имеет безусловный характер.
В индексном ряду с постоянными весами значительно легче изменять базу расчета.
В то же время все индексы качественных показателей исчисляются по весам – соизмерителям отчетного периода, т.е. являются индексами с переменными весами. Для таких индексных рядов указанная взаимосвязь не выполняется. Однако в статистических исследованиях иногда приходится прибегать к перемножению цепных индексов с переменными весами для того, чтобы получить базисный индекс. При этом вследствие системы переменных весов результат содержит некоторую ошибку. Величина этой ошибки определяется расхождением двух разновзвешенных индексов:
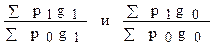 .
.
Количественно эта ошибка зависит от:
А) коэффициентов вариации индивидуальных индексов «р»;
Б) вариации индивидуальных индексов «g»;
В) а также от тесноты зависимости (коэффициента корреляции) между индивидуальными индексами «р» и «g».
Чем меньше будет каждая из этих величин, тем меньше будет их произведение, а, следовательно, ошибка в оценке величины базисного индекса путем перемножения цепных индексов с переменными весами.






