Вращающиеся валы и оси обычно нагружены со стороны элементов, непосредственно участвующих в передаче движения (шкивы, звёздочки, зубчатые колёса, барабаны и т.п.), силами, направление действия которых по отношению к опасным сечениям вала постоянно меняется из-за вращения самих этих сечений. Кроме того, поперечные сечения валов, как элементов, передающих крутящий момент, испытывают и касательные напряжения, которые при реверсировании движения тоже меняют своё направление. Чрезмерный изгиб валов в поперечном направлении приводит к нарушению нормальной работы элементов, непосредственно передающих движение, и, вследствие поворота поперечных сечений цапф, подшипниковых узлов. В силу этого основными критериями работоспособности валов и вращающихся осей являются усталостная прочность и жёсткость.
При расчете осей и валов их прочность оценивают по коэффициенту запаса усталостной прочности, а жёсткость – величиной прогиба под действием рабочих нагрузок, углом поворота отдельных сечений (чаще всего опорных сечений цапф) в плоскости осевого сечения и углом закру чивания поперечных сечений под действием крутящего момента.
Таким образом, основными расчётными нагрузочными факторами являются крутящие T и изгибающие M моменты. Влияние на прочность вала растягивающих и сжимающих сил само по себе незначительно и в большинстве случаев не учитывается.
Расчёт вала должен, как правило, включать, по меньшей мере, три основных этапа: проектировочный расчёт, формирование расчетной схемы и проверочный расчёт. В некоторых случаях к этим трём этапам расчёта добавляются и другие, например, для быстроходных валов часто выполняют расчёт на колебания (расчёт вибрационной стойкости), для валов, работающих в широком температурном диапазоне, расчёт тепловых деформаций, теплостойкости и т.п.
Проектный расчёт валов производят только на статическую прочность по передаваемому крутящему моменту T. При этом расчёте определяется минимальный из всех диаметр вала (чаще всего таковым является диаметр выходного конца вала), а с целью компенсации неучтённых изгибных нагрузок и других факторов (концентраторов напряжений, шпоночных канавок и т.п.), влияющих на прочность вала, принимают заниженные значения допускаемых касательных напряжений [t]к» (0,025…0,030)× sВ.
В этом случае диаметр вала определяется по известной зависимости сопромата
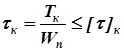; (9.1)
где tк – максимальные касательные напряжения, действующие в наружных волокнах опасного сечения вала; Tк - крутящий момент, передаваемый через это сечение; Wп – полярный момент инерции рассматриваемого сечения.
Учитывая, что большинство валов в машиностроении имеет круговое либо кольцевое (для полых валов) поперечное сечение, после представления полярного момента инерции сечения через его диаметры из (9.1) получаем
; (9.2)
где D – внешний диаметр вала; b = d/D – относительный диаметр осевого отверстия полого вала (d – абсолютное значение диаметра этого отверстия). При этом можно отметить, что для b £ 0,5 расчёт полого вала как сплошного даёт погрешность менее 2,5% от диаметра вала, значительно перекрываемую за счёт занижения допускаемых напряжений. Отсюда следует возможность рассчитывать толстостенные валы как сплошные (выражение в скобках принять равным 1).
Полученный таким расчётом диаметр вала округляют до ближайшего большего значения из рядов нормальных линейных размеров по ГОСТ 6636-69. Диаметры других ступеней вала устанавливают из конструктивных соображений в процессе эскизного проектирования механизма.
Формирование расчётной схемы возможно только после полного конструктивного оформления вала на основе проектного расчёта, эскизного проектирования, подбора подшипников и расчёта конструктивных элементов, участвующих в передаче вращающего момента.
При формировании расчётной схемы вал обычно представляют в виде балки, лежащей на опорах (число опор обычно равно числу подшипников), одна из которых считается закреплённой в осевом направлении.
Если вал закреплён в корпусе посредством радиальных или сферических, шариковых либо роликовых подшипников, опору считают расположенной на геометрической оси вала в точке пересечения с поперечной осью симметрии подшипника.
При использовании радиально-упорных подшипников за точку опоры принимают точку продольной геометрической оси вала, лежащую на её пересечении с нормалью к поверхности качения, проведённой через центр тел качения.
Для подшипников скольжения, а также при установке сдвоенных подшипников качения за точку опоры принимают точку, лежащую на оси вращения и расположенную на расстоянии, равном 0,2…0,3 длины подшипника (суммарной длины пары подшипников качения) от его (их) внутренней кромки.
Силы, действующие на вал со стороны ступиц шкивов, шестерён, звёздочек и других подобных элементов, считают приложенными по середине ступицы, если последняя расположена между подшипниками, и на расстоянии 0,25…0,3 длины ступицы со стороны её внутреннего края, при её консольной установке (то есть на конце вала).
Величину и направление сил, действующих на вал со стороны элементов, непосредственно передающих вращательное движение, определяют по результатам расчёта соответствующей передачи, а величину сил от муфт, возникающих вследствие несоосности валов, определяют по формулам, представленным в расчёте муфт выбранной конструкции. Направление поперечных сил, действующих на вал в плоскости его поперечного сечения со стороны муфт, может быть любым, поэтому при формировании расчётной схемы принимают наиболее неблагоприятное направление этих сил с точки зрения прочности вала. Так, например, при формировании расчётной схемы вала, представленного на рис. 9.7, если его наружный конец будет снабжён муфтой, силу на этом конце со стороны муфты следует направить в направлении, совпадающем с направлением тангенциальной составляющей силы, действующей на зубья шестерни. Именно в этом случае нагружение вала поперечными силами будет наиболее неблагоприятным с точки зрения прочности и жёсткости вала.
Проверочный расчёт валов производится после формирования расчётной схемы и уточнения всех нагрузок, как по величине, так и по направлению. Этот вид расчёта предусматривает проверку вала на статическую прочность по наибольшей возможной кратковременной нагрузке и на усталостную прочность при переменных напряжениях. В последнем случае вычисляется коэффициент фактического запаса прочности в предположительно опасных сечениях, которые предварительно намечаются согласно эпюре моментов с учётом размеров поперечного сечения и зон концентрации напряжений.
На статическую прочность валы рассчитывают по наибольшей возможной кратковременной нагрузке с учётом динамических и ударных воздействий. Для валов, работающих в условиях кручения и изгиба, продольными усилиями можно пренебречь. В этом случае эквивалентное напряжение в наружном волокне вала
; (9.3)
где sи – максимальное напряжение от изгиба; tк – наибольшее напряжение от кручения. Поскольку sи = Mи / Wи, а tк = Tк / Wк, где Wи и Wк момент сопротивления вала в опасном сечении изгибу и кручению, соответственно, и учитывая, что
(9.4)
после подстановки всех значений в (9.3) получим
. (9.5)
Зная эквивалентные напряжения, можно проверить запас прочности по пределу текучести
, (9.6)
где нормативный запас прочности [n] обычно принимают равным 1,2…1,8.
Опасные сечения (как правило, на прочность исследуются несколько подозрительных сечений), в которых необходимо установить величину запаса прочности, определяются по максимальным изгибающим и крутящим моментам с учётом размеров сечений. Максимальные значения моментов находят после построения эпюр изгибающих и крутящих моментов. При наличии сил, действующих на вал в разных плоскостях, эти силы проецируют на координатные оси и строят эпюры изгибающих моментов в координатных плоскостях, после чего выполняют геометрическое суммирование изгибающих моментов.
Проверочный расчёт на сопротивление усталости проводят по максимальной длительно действующей нагрузке без учёта кратковременных пиковых нагрузок (возникающих, например, во время пуска), слабо влияющих на возникновение усталостных разрушений, поскольку такие нагрузки занимают малое число циклов нагружения. Для каждого опасного сечения, установленного в соответствии с эпюрами изгибающих и крутящих моментов, определяют расчётный коэффициент запаса прочности S и сравнивают его с допускаемым [S] (обычно принимают [S] = 1,2…2,5) по выражению
; (9.7)
где Ss и St - коэффициенты запаса прочности по нормальным и касательным напряжениям соответственно:
(9.8)
где s-1 и t-1 – пределы выносливости для материала вала при симметричном цикле изгиба и кручения; sа и tа – амплитуды изменения напряжений изгиба и кручения; sm и tm – средние значения за цикл тех же напряжений; ys и yt - коэффициенты чувствительности материала вала к асимметрии цикла напряжений (yt» ys / 2; 0,05£ys£ 0,2); KsD и KtD – коэффициенты снижения пределов выносливости по изгибу и кручению, определяемые по формулам:
(9.9)
в которых Ks и Kt - эффективные коэффициенты концентрации напряжений для данного сечения вала в зависимости от его формы, Kd – коэффициент влияния абсолютных размеров поперечного сечения, KF – коэффициент влияния шероховатости поверхности вала (для посадок с натягом KF» 1), Kv – коэффициент, учитывающий упрочнение поверхности (при отсутствии поверхностного упрочнённого слоя Kv» 1). Перечисленные коэффициенты устанавливаются по справочным данным с учётом материала и конструкции рассчитываемого вала.
Пределы выносливости s-1 и t-1 для улучшенных или нормализованных углеродистых и углеродистых легированных сталей с известным пределом прочности sВ, при симметричном цикле изгиба и кручения можно определить по эмпирическим зависимостям
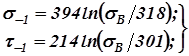(9.10)
где все значения напряжений в Н/мм2 (МПа).
Амплитудные значения нормальных sа и касательных tа напряжений вычисляют согласно известным выражениям
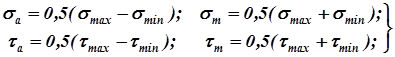(9.11)
где smax и smin, tmax и tmin – максимальные и минимальные значения нормальных и касательных напряжений в точках наружных волокон опасного сечения вала, которые, в свою очередь, вычисляются по соответствующим формулам сопротивления материалов
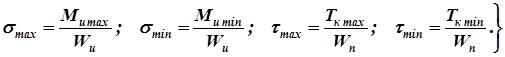(9.12)
Типичными являются такие условия нагружения, когда напряжения от изгиба валов имеют чисто симметричный характер, то есть максимальный и минимальный изгибающие моменты в данном сечении равны по величине и противоположны по направлению. Для таких условий, а средние напряжения за цикл sm = 0.
