Геометрию, кинематику и динамику червячной передачи рассмотрим на примере передачи с архимедовым червяком.
Геометрические характеристики червячной передачи связаны между собой соотношениями, во многом аналогичными соотношениям зубчатых передач.
Основным стандартизованным параметром червячной передачи является модуль m (измеряется в мм), осевой для червяка и окружной (торцовый) для червячного колеса. Поскольку делительный диаметр червяка невозможно связать с числом его заходов z1 (витки червяка нарезаются вдоль его оси, а не по окружности, как у зубчатого колеса), для определения делительного диаметра червяка вводится специальный коэффициент диаметра червяка q, показывающий число модулей, укладывающихся в делительный диаметр.
Свои особенности имеет и геометрия венца червячного колеса. В виду того, что образующая делительной поверхности венца червячного колеса (рис. 6.4) имеет дугообразную форму и, следовательно, в разных точках разное удаление от оси вращения колеса, все основные размерные показатели (делительный диаметр, высота зуба и др.) измеряются в серединной плоскости, проходящей через геометрическую ось червяка.
Учитывая изложенное, модуль с делительными диаметрами червяка и червячного колеса связан соотношениями
. (6.1)
Расстояние, измеренное между одноименными поверхностями двух соседних гребней нарезки червяка, называют расчетным шагом нарезки червяка. Расчетный шаг нарезки червяка связан с модулем червячного зацепления соотношением, аналогичным таковому для зубчатого зацепления:
. (6.2)
Расстояние, измеренное между одноименными поверхностями двух соседних гребней, принадлежащих общей винтовой линии нарезки червяка, называют ходом витка червяка. Из определения следует, что расчетный шаг p и ход витка pz связаны соотношением
. (6.3)
Высота головок витков червяка и зубьев червячного колеса также как и в зубчатом зацеплении равна модулю зацепления (ha1 = ha2 = m), а высота ножек с целью исключения возможности утыкания головки зуба в дно впадины, как и в конических передачах, на 20% больше модуля зацепления (hf1 = hf2 = 1,2m). Тогда диаметр вершин витков (внешний диаметр) червяка da1 и диаметр вершин зубьев червячного колеса da2 могут быть найдены по выражениям
; (6.4)
а диаметр впадин витков (внутренний диаметр) червяка df1 и диаметр впадин зубьев червячного колеса df2 (рис. 6.4) - по выражениям
. (6.5)
Измеренный в плоскости осевого сечения угол a между касательной к боковой поверхности витков червяка и нормалью к оси его вращения для архимедовых червяков является величиной постоянной, стандартизован и равен 20°. Следовательно, угол между двумя касательными к противоположным боковым поверхностям одного витка (угол заострения гребня) составляет 2a или 40°.
Длина нарезанной части червяка b1 зависит от числа его заходов и выбирается по эмпирической формуле
при числе витков червяка z1 = 1 и z1 = 2 
; (6.6)
а при числе витков червяка z1 = 4 
. (6.7)
Отношение хода витка к длине делительной окружности червяка – есть величина тангенса угла подъёма g винтовой линии нарезки червяка
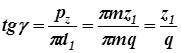(6.8)
Особенностью червячного колеса является то, что диаметр вершин зубьев da2 не самый большой его диаметр. Максимальный диаметр червячного колеса daM2 устанавливается в некоторой степени произвольно. Увеличение этого диаметра способствует увеличению площади контактной поверхности зубьев колеса, а следовательно, и снижению контактных напряжений на этой поверхности, возникающих в процессе работы передачи. Однако чрезмерное его возрастание приводит к заострению периферийных участков зуба и исключению их из передачи рабочих нагрузок вследствие повышенной гибкости. Поэтому максимальный диаметр зубьев червячного колеса daM2 имеет ограничение сверху по соотношению
. (6.9)
Ширину зубчатого венца червячного колеса b2 выбирают по стандартному ряду размеров. При этом размер b2 должен удовлетворять соотношению
при числе витков червяка z1 = 1 и z1 = 2 
; (6.10)
а при числе витков червяка z1 = 4 
. (6.11)
При прочностных расчетах червячной передачи возникает потребность в знании условного угла 2d охвата витков червяка зубьями червячного колеса. Этот угол определяют по точкам пересечения боковых (торцовых) поверхностей червячного колеса с условной окружностью, диаметр которой равен 
, следовательно
. (6.12)
Межосевое расстояние для несмещенной червячной передачи определяется по формуле
. (6.13)
В червячной передаче, в отличие от зубчатой, окружные скорости витков червяка v1 и зубьев червячного колеса v2 различны как по величине, так и по направлению. Витки червяка при его вращении получают скорость v1, направленную по касательной к его начальной окружности, а зубья червячного колеса движутся совместно с винтовой линией параллельно оси червяка со скоростью v2. За один оборот червяка червячное колесо повернется на угол, охватывающий число зубьев колеса, равное числу заходов червяка. Эти простые наблюдения позволяют записать следующую зависимость для вычисления передаточного числа червячной передачи
. (6.14)
Геометрическая сумма скоростей v1 и v2 равна скорости относительного движения витков червяка по отношению к зубьям колеса. План скоростей, построенный для зацепления, позволяет записать следующие зависимости
. (6.15)
Таким образом, скорость скольжения витков червяка по зубьям червячного колеса является наибольшей по сравнению с тангенциальными скоростями движения витков червяка и зубьев червячного колеса.
Коэффициент полезного действия hз червячного зацепления можно вычислить как КПД винтовой кинематической пары:
при ведущем червяке 
; (6.16)
а при ведущем червячном колесе 
; (6.17)
где 
- угол трения в червячной кинематической паре, а f коэффициент трения для материалов витков червяка и зубчатого венца червячного колеса.
При g £ r hзо = 0 передача движения от червячного колеса к червяку становится невозможной – происходит самоторможение. Свойство самоторможения обратного движения широко используется в лебёдках и грузоподъёмных механизмах. Однако необходимо отметить, что у таких самотормозящихся механизмов и в прямом направлении передачи движения КПД невелик.
В червячной передаче сила Fn, действующая со стороны червяка, воспринимается, как правило, не одним, а несколькими зубьями. Однако, также как и в зубчатых передачах, при выполнении расчетов эту силу принято располагать в полюсе зацепления (рис. 6.6, а). Эту силу не трудно разложить по правилу параллелограмма на три взаимно перпендикулярных составляющих Ft1, Fr1 и Fa1. Далее, согласно третьему закону Ньютона устанавливаем, что Ft2 = Fa1, Fa2 = Ft1 и Fr2 = Fr1.
Тангенциальные силы на червяке и червячном колесе наиболее удобно вычислить через вращающие моменты на соответствующих валах, тогда
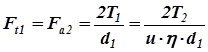(6.18)
и 
. (6.19)
Радиальные силы на червяке и колесе
. (6.20)
ТЕМА 4.
РЕМЕННЫЕ ПЕРЕДАЧИ.
Ременная передача – это механизм, предназначенный для передачи вращательного движения посредством фрикционного взаимодействия или зубчатого зацепления замкнутой гибкой связи – ремня с жесткими звеньями – шкивами, закрепленными на входном и выходном валах механизма.
Ременная передача состоит из двух или большего числа шкивов, насаженных на валы, участвующие в передаче вращательного движения, и гибкой связи, называемой ремнем, которая охватывает шкивы с целью передачи движения от ведущего шкива ведомому (или ведомым) и взаимодействует с ними посредством сил трения или зубчатого зацепления.
Основную часть лекции посвятим фрикционным ременным передачам, поэтому далее под термином ременная передача, если это не будет оговорено особо, будем понимать именно фрикционную передачу.
Ременные передачи трением – наиболее старый и простой по конструкции вид передачи. Эти передачи и в настоящее время находят достаточно широкое применение, они широко применяются на быстроходных ступенях привода (передача вращения от электродвигателей к последующим механизмам). В двигателях внутреннего сгорания МГКМ ременные передачи применяются для привода вспомогательных агрегатов (вентилятор, насос системы водяного охлаждения, электрический генератор), а зубчатоременная передача применяется в некоторых автомобильных двигателях для привода газораспределительного механизма.
Достоинства ременных передач: 1. Простота конструкции и низкая стоимость. 2. Возможность передачи движения на достаточно большие расстояния (до 15 м). 3. Возможность работы с большими скоростями вращения шкивов. 4. Плавность и малошумность работы. 5. Смягчение крутильных вибраций и толчков за счет упругой податливости ремня. 6. Предохранение механизмов от перегрузки за счет буксования ремня при чрезмерных нагрузках.
Недостатки ременных передач: 1. Относительно большие габариты. 2. Малая долговечность ремней. 3. Большие поперечные нагрузки, передаваемые на валы и их подшипники. 4. Непостоянство передаточного числа за счет проскальзывания ремня. 5. Высокая чувствительность передачи к попаданию жидкостей (воды, топлива, масла) на поверхности трения.
Классификация ременных передач:
1. По форме поперечного сечения ремня: плоскоременные (поперечное сечение ремня имеет форму плоского вытянутого прямоугольника, рис. 2.1.а); клиноременные (поперечное сечение ремня в форме трапеции рис. 2.1.б); поликлиноременные (ремень снаружи имеет плоскую поверхность, а внутренняя, взаимодействующая со шкивами, поверхность ремня снабжена продольными гребнями, выполненными в поперечном сечении в форме трапеции рис. 2.1.г); круглоременные (поперечное сечение ремня имеет форму круга рис. 2.1.в); зубчатоременная (внутренняя, контактирующая со шкивами, поверхность плоского ремня снабжена поперечными выступами, входящими в процессе работы передачи в соответствующие впадины шкивов).
2. По взаимному расположению валов и ремня: с параллельными геометрическими осями валов и ремнем, охватывающим шкивы в одном направлении – открытая передача (шкивы вращаются в одном направлении); с параллельными валами и ремнем, охватывающим шкивы в противоположных направлениях – перекрестная передача (шкивы вращаются во встречных направлениях); оси валов перекрещиваются под некоторым углом (чаще всего 90°) – полуперекрестная передача.
3. По числу и виду шкивов, применяемых в передаче: с одношкивными валами; с двушкивным валом, один из шкивов которого холостой; с валами, несущими ступенчатые шкивы для изменения передаточного числа (для ступенчатой регулировки скорости ведомого вала).
4. По количеству валов, охватываемых одним ремнем: двухвальная, трех -, четырех - и многовальная передача.
5. По наличию вспомогательных роликов: без вспомогательных роликов, с натяжными роликами; с направляющими роликами.
Геометрические соотношения в ременной передаче рассмотрим на примере открытой плоскоременной передачи. Межосевое расстояние а – это расстояние между геометрическими осями валов, на которых установлены шкивы с диаметрами D1 (он, как правило, является ведущим) и D2 (ведомый шкив). При расчетах клиноременных передач для ведущего и ведомого шкивов используются расчетные диаметры dр1 и dр2. Угол между ветвями охватывающего шкивы ремня - 2g, а угол охвата ремнем малого (ведущего) шкива (угол, на котором ремень касается поверхности шкива) a1. Половинный угол между ветвями составит
, (2.12)
а так как этот угол обычно невелик, то во многих расчетах допустимым является приближение g» sing, то есть
. (2.13)
Используя это допущение угол охвата ремнем малого шкива можно представить в следующем виде
(2.14)
в радианной мере, или
(2.15)
в градусах.
Длину ремня при известных названных выше параметрах передачи можно подсчитать по формуле
. (2.16)
Однако, весьма часто ремни изготавливаются в виде замкнутого кольца известной (стандартной) длины. В этом случае возникает необходимость уточнять межосевое расстояние по заданной длине ремня
. (2.17)
С целью обеспечения стабильности работы передачи обычно принимают
для плоского ремня 
,
а для клинового –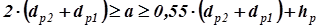 
,
где hp – высота поперечного сечения ремня (толщина ремня).
В процессе работы передачи ремень обегает ведущий и ведомый шкивы, чем короче ремень (чем меньше Lp) и чем быстрее он движется (чем больше его скорость Vp), тем чаще происходит контактирование его рабочей поверхности с поверхностью шкивов и тем интенсивнее он изнашивается. Поэтому отношение Vp / Lp (его размерность в системе СИ – с-1) характеризует долговечность ремня в заданных условиях его работы – чем больше величина этого отношения, тем ниже при прочих равных условиях долговечность ремня. Обычно принимают
для плоских ремней Vp / Lp = (3…5) с-1,
для клиновых - Vp / Lp = (20…30) с-1.
