27.Гильбертово пр-во.Разлож-е эл-ов гильбертова пр-ва по ортонормир.сис-ам. Общий вид лин-го непрерыв. функционала в гильбертовом пр-ве. Опр. Пусть X-векторное пр-во над полем K(R,C).Ф-ия<*,*>:X 
X→K наз. скаляр.произведением на Х,если: 1. "хÎХ <x,x> ≥0, <x,x>=0 <=> x=0; 2. "х,yÎХ <x,y>=<y,x> 3. "х,yÎХ,"λÎR <λx,y>=λ<x,y>(однород.по 1-му арг-ту) 4. "х,y,zÎХ <x+y,z>=<x,z>+<y,z>(аддитив.по 1-му арг-ту). Пр. Х=Rn:<x,y>=x1*y1+…+xn*yn. Утв1. Если<*,*>-скаляр.произв-е,то 
норма на Х(1. φ(λх)=|λ|φ(х), 2. φ(х+y)≤φ(х)+φ(y)) Опр. Сис-ма вект-ов наз. ортонормир-ой,если < l k; l m>=δkm={1,k=m;0,k≠m.Сис-ма век-ов 
наз. ортонормир,если таковой явл. 
конечная подсис-ма для таковой сис-мы.Полное лин.нормированное пр-во наз. банаховым. Опр. Банахово пр-во Х с нормой||*||наз. гильбертовым пр-вом,если в нем для"f,gÎХ опр.скаляр.произвед.(f,g),уд.усл-ям: (f,g)=(g,f),(αf1+βf2,g)=α(f1,g)+β(f2,g)(аддитивность). Опр. Эл-ты x,y из гильбертова пр-ва Х наз. ортогональными,если<x,y>=0. Т. Пусть X–гильберт.пр-во(X,<,>), -ортонормир.сис-ма вект-ов в X,тогда: 1. справедл. нер-во Бесселя:∑k=1∞│ck│2≤║x║2, 2. ряды Фурье сх-ся к т-ке x 
X óвыполн.рав-во Парсеваля–Стеклова: ∑k=1∞│ck│2=║x║2,где ck-коэф.Фурье,ряд ∑k=1∞ck l k Фурье. Опр. Сис-ма вект-ов l k наз.макс-ой в гильберт пр-ве X,если из усл.,что 
k N, <x, l k>=0 
x=0. Опр. Сис-ма век-ов l k наз. полной в гильберт пр-ве X,если мн-во всех конечных лин-ых комбинаций век-ов этой сис-мы всюду плотно в гильберт пр-ве. Т. Пусть X гильберт.пр-во, -ортонормир.сис-ма,тогда эквивалентны утверждения: 1) данная сис-ма явл.базисом в X; 2) сис-ма максимальна; 3) справедлив.рав-во Парсеваля-Стеклова; 4) сис-ма явл.полной. Т.(Рисса) Пусть Х-гильбертово пр-во,f:X→R–линейный ограниченный ф-ал,тогда 
эл-т y из Х,что 
x X справедливо:(f,x)=<x,y>.
28.Приводим.и неприводим.мн-ны над полем хар-ки 0.Непривод-ть мн-нов над поле C,Q,R. Кольцо -непустое мн-во К эл-тов произвол.природы с опр.на нем бинарн.операц.+и*,если выполн.усл.:алгебра<К,+>-абелева группа,умнож.ассоциативн a,b,cÎK а(bc)=(ab)c,умнож дистрибутив.относ+,т.е.а(b+c)=ab+ac.А К[x](кольцо многочл.) - расшир К и содерж.перем. х,т.е.КÎК[x].Хар-ка кольца–наименьшее nÎN. Если не 
такого n, то хар-ка кольца=0.Мн-н f(x) из кольца P[x] наз приводимым над полем Р, если его можно представить в виде произведения 2-х мн-нов из кольца Р[х],каждый из кот.степени не ниже 1-й.Если такое представление не возможно,то f не приводим над Р. Св-ва неприводимых мн-в: 1) Если f/P,где f,PÎP[x] неприводимые,то f и P совпадают с точностью до постоянного множителя; 2) Пусть f– любой мн-енÎР[x], Р–неприводимый, тогда f/P или (f,P)=1(взаимно простые). 3) Если произведение мн-ов из кольца Р[x] делится на неприводимый мн-н,то хотябы 1 из сомножителей делится на Р. 4) Если произведение неприводимых мн-ов из кольца Р[x] делится на неприводимый мн-ен Р,то хотябы 1 из сомножителей совпадает с Р с точностью до постоянного мн-ля. Т. (о неприводимых мн-ах). Всякий мн-ен f(x) степени не ниже 1-ой из кольца Р[x] м.б.разложен в произведение неприводим.мн-ов из этого кольца,и это разлож-е ед-но с точностью до порядка следования сомножителей и до постоянного множителя. Д-во. М-д мат.индукции(n-степень многочлена). 1. n=1. Мн-н 1-й степени неприводим над 
полем, значит f можно разложить в произведение неприводим.мн-ов,но в этом произведении только 1 множитель,т.е. f=f. 2. Предположим теорема верна для всех мн-ов, степень кот.£n.Док-м для n+1. А) f степени n+1 не приводим над РÞон разложим в произведение неприводимых мн-ов, но в этом произведении только 1 множитель. Б) f степени n+1 приводим над РÞf=f1*f2, f1,f2ÎP[x],где deg(f1)£n и deg(f2)£n.Т.к.степени мн-ов f1,f2£n,то по индуктивному предположению для мн-ов f1,f2 верна теорема,т.е. f1,f2 м.б.представлены в виде произведения непривод-ых мн-ов.Док-м един-ть такого разлож-я.Предполож. противное:кроме разложения f=p1p2…ps существует f=q1q2…qs+m.; p1p2…ps=q1q2…qs+m правая часть делится на р1.По св-ву 4 хотя бы 1 из этих мн-ов совпадает с р1 с точностью до постоянного множителя,наприм., q1, т.е. q1=с1р1, с1ÎР. p2…ps=с1q2…qs+m Аналогично q2=с2р2, с2ÎР. И т.д. После s сокращений получим:е=с1с2…сsqs+1…qs+m.Т.к степень левой части = 0, то в правой части м.б.только с1 с2… сs. Т.е.в данных разлож-х одинак-е кол-во мн-ов и они могут различаться только порядком следования и постоянными множ-ми. ч.т.д. Разлож-е f(x)=а* 
, где 
все различные множ-ли Р(х), аÎP, a≠0 наз. каноническим разлож f(x)ÎP(х) над полем Р. Всякий мн-н f(x) степени n³1 над полем комплексных чисел им. хотя бы 1 комплексный корень. Неприводим. над полем комплексных(С)чисел являются только мн-ны 1-ой степени. Неприводим. над полем действит-ых(R) чисел явл-ся только мн-ны 1-ой и 2-ой степени,кот. не им. действит. корней.Всякий мн-ен f(x), n³1 над полем R раскладывается в произведение мн-ля an, явл-ся старшим коэф-ом f, и неприводимых мн-ов со старшим коэф-ом 1, причем лин-й мн-н им.1 дейсв. корень, а квадратичный–2 комплексно-сопряженных. И это разлож-е един-но с точностью до порядка следования. Мн-н с рациональными коэф-ми 2-й или 3-й степени разложим над полем Q на непривод.мн-лиó,когда он им. хотя бы 1 рац.корень. Кр.Эйзенштейна: Если для мн-на f(x)= 
с целыми коэф-ми можно подобрать такое простое число р, что: 1) аn не÷на р; 2) (а0,а1…аn-1)÷на p; 3) а0 не ÷ на 
,то f(x) не приводим над полем Q. Поле –комутативн. кольцо с 1-цей е≠0 в кот кажд.ненулевой эл-т обратим.(Z не поле)
29.Лин-е пр-во.ЛЗ и ЛНЗ сис-мы век-ов... К¹Æ эл-ов любой природы, с заданными на нем операциями + и ´ наз кольцом относительно сложения и умножения,если: 1) К –абелева группа по сложению; 2) на К умнож-е ассоциативно; 3) На К вып-ся дистрибутивный з-н умнож-я относительно слож-я [(a+b)c=ac+bc]. Коммутативное кольцо Р с ед-цей е¹0,наз полем, если в нем каждый ненулевой эл-т им.обратный. Пусть Р– 
поле.Его эл-ты бу.наз-ть скалярами. V¹Æ наз. линейным(векторным) пр-ом над полем Р,если выполн-ся следующие усл-я: 1) на V опр-на операция сложения: "a,bÎV $!(a+b)ÎV;2)V–абелева группа по слож-ю(слож-е ассоциативно, коммутативно, 
хотя бы 1 правый нейтральный и симметричный эл-т относительно слож-я); 3) опр-но умнож-е эл-ов из V на скаляр из поля Р:"aÎР,"aÎV:$!aaÎV; 4) "a,bÎР,"aÎV:(ab)a=a(ba); 5) "a,bÎР,"aÎV:(a+b)a=aa+ba; 6) "aÎР,"a,bÎV: a(a+b)=aa+ab; 7) "aÎV:1*a=a. Пр. вектор-го пр-ва:Рn={(a1,a2,…an)|aiÎP},Rn,Cn. b=a1a1+a2a2+…+anan наз лин-ой комбинацией вект-в α1,α2,…αn, aiÎP–коэф-ты лин-ой комбинации.Сис-ма вект-в(a1,a2,…an)ÎV наз. линейно зависимой (ЛЗ),если 
скаляры a1,a2,…anÎP не все из кот.=0,такие что a1a1+a2a2+…+anan=0.Если рав-во выполняется только тогда,когда все aI=0,то сис-ма линейно независима (ЛНЗ). Т. (о ЛЗ). Сис-ма век-ов (a1,a2,…am)ÎV, m>1 ЛЗó,когда хотя бы 1 век-р из этой сис-мы явл-ся лин-ой комбинацией остальных век-ов. Док-во. 1) Пусть сис-ма ЛЗ 
скаляры a1,a2,…anÎP не все из кот.=0,такие что a1a1+a2a2+…+anan=0.Пусть a1¹0,тогда а1=(-a2/a1)a2+…+(-an/a1) an.В др.обозначениях: а1=b2a2+…+bnan,где коэф-ты при аiÎР,т.о.получили линейную комбинацию век-ов. 2) Пусть а1 явл-ся лин-ой комбинацией остальных век-ов, Тогда 1а1+(-b2)a2+…+(-bn)an, где коэф-т при а1 отличен от 0Þсис-ма ЛЗ.ч.т.д. Сл.1. Всякая сис-ма,содержащая нуль-вектор ЛЗ. Сл.2. Если подсис-ма сис-мы ЛЗ,то и вся сис-ма ЛЗ. Сл.3. Если сис-ма ЛНЗ,то любая ее подсис-ма ЛНЗ. Пусть дано лин-е вектор-е пр-во L над полем Р.(Нулев. пр-во не им.базиса). Базисом лин-го вектор-го пр-ва L над полем Р наз любая ЛНЗ сис-ма вект-в,такая что ч/з нее линейно выражается любой вектор пр-ва. Кр.базиса. ЛНС сис-ма вект-ов из пр-ва L над полем Р явл-ся базисом ó,когда она явл-ся максимально ЛНЗ(сист становится ЛЗ при прибавлении к ней любого вектора из L). Размерностью пр-ва L над полем Р наз.число векторов его базиса. Существуют конечномерное и бесконечномерное пространства. Не пустое мн-во М лин-го пр-ва L над полем Р наз.подпр-вом пр-ва L,если оно само образует пр-во относительно сложения и умножения вектора на скаляр. Кр.подпр-ва. Не пустое мн-во М лин-го пр-ва L над полем Р образует подпро-во ó,когда 1) "a,bÎV^$!(a+b)ÎМ; 2) "aÎР,"aÎМ: $!aaÎV. Мн-во лин-ых комбинаций векторов a1,a2,…anÎL над полем Р наз линейной оболочкой, натянутой на векторы a1,a2,…an. Размерностью линейной оболочки явл-ся ранг сис-мы векторов a1,a2,…an.
30.Скаляр-е,вектор-е и смешан-е произвед-е вект-ов 3-хмерного евклидова пр-ва. Прилож-я к реш-ю з-ч. Век-р –направл-ый отрезок. 2 век-ра коллинеарны если 
прямая,кот.они оба параллельны. 3 век-ра компланарны,если 
пл-сть,кот.все 3 параллельны.Непустое мн-во V наз. векторным(лин)пр-вом над полем Р,если вып-ся след усл-я: 1) на V опр-на операция слож-я: "a,bÎV:$!(a+b)ÎV; 2) V–абелева группа по слож-ю(слож-е ассоциатив.,коммутатив., хотя бы 1 правый нейтральный и симметричный эл-т относительно слож-я); 3) определено умнож-е эл-ов из V на скаляр из поля Р:"aÎР,"aÎV:$!aaÎV; 4) "a,bÎР,"aÎV:(ab)a=a(ba); 5) "a,bÎР,"aÎV:(a+b)a=aa+ba; 6) "aÎР, "a,bÎV:a(a+b)=aa+ab; 7) "aÎV:1*a=a. Пусть L-лин пр-во над полем R.Отобр-ие L2→R наз. скаляр.умнож-ем в-ров,а образ пары в-ров 
ÎL наз. скаляр.произвед-ем и обознач. 
, если вып-ся след усл-я: 1. "a,bÎL:ab=ba (коммутативно); 2. "a,b,cÎL:(a+b)c=ac+bc(дистрибутивно); 3. "a,bÎL,αÎL:(αa)b=α(ab) (ассоциативно); 4. "αÎL,α≠0:α2>0. Св-ва век-го умнож-я: 1. век-ое произвед-е век-ов=0 
в-ры коллинеарны. 2. При изменении порядка сомножителей вект-ое произвед-е изменяет знак на противоположный(св-во антикоммутативно a*b=-b*a); 3. Век-ое умнож-е ассоциативно относительно числового множителя (αa)b=α(ab); 4. Век-ое умнож-е дистрибутивно относительно слож-я век-ов (a+b)c=ac+bc. 2-а ненулевых в-ра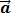 
и 
перпендик-ны,если 
=π/2. Скаляр.произвед-ем 2-х в-ров наз число,равное произвед-ю длин в-ров на cos угла м/д ними 
,где 
Вект-ое пр-во L над полем R,в к-ом задано скаляр.произвед-е наз. евклидовым пр-вом (Е). 2-а в-ра 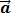и наз. ортогональными,если 
,т.е.(a ^ b). С-ма в-ров (a1,a2,…an)ÎЕ наз. ортогональной,если ее в-ры попарно ортогональны. 2-а в-ра 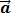и наз. ортонормированными,если они ортогональны и нормированы(
).С-ма в-ров (a1,a2,…an)ÎЕ наз. ортонормированной,если она ортогональна и ее в-ры нормированы.Базис (a1,a2,…an)ÎЕ наз. ортогональным,если сис-ма a1,a2,…an ортогональна(ортонормирован.,если с-ма ортонормированна). Т. Скаляр.прозвед-е в-ров 
и зад.своими корд-тами в ортонормированном базисе взаимно перпендикулярны a1b1+a2b2+…+anbn=0. Т. Скаляр.произвед-е 2-х в-ров 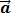и из пр-ва Е разложенных по базису=сумме произведений одноименных корд-т базис ортонормированный.Выраж-е векторного произвед-я ч/з координаты век-ов: 
. Площадь треугольника по известным координатам его вершин A(x1,y1), B(x2,y2),C(x3,y3) вычисляется по формуле 
.Смешанным произвед-ем 3-х век-ов 
наз.число,равное 
.Обознач-ся 
. Св-ва смешан-го произвед-я: 1. (геометр-ий смысл смешан.произвед-я)Смешанное произвед-е 3-х век-ов с точностью до знака=объёму параллелепипеда,построен.на этих век-ах,как на рёбрах,т.е. 
,т.о. 
и 
2. Для"век-ов 
справедливо рав-во 
; 3. При перестановке"2-х сомножителей смешан-е произвед-е меняет знак. 4. Смешан.произвед-е 
ó, когда 1-н из сомножителей=0 или век-ры компланарны. 5. Необход.и достаточ. усл-ем компланарности век-ов явл-ся рав-во нулю их смешан.произвед-я().В координатной форме условие компланарности имеет вид: 
.
31. Плоскость и прямая в прастранстве. 1. Ур-ние пл-ти,заданное т-кой M0(x0,y0,z0) и направл-щим подпр-вом L с базисом образованным в-ми 
, 
: 
2. Ур-ние пл-ти, задан. 3-я т-ми M1(x1,y1,z1),M2(x2,y2,z2), M3(x3,y3,z3): 
3. Ур-ние пл-ти, заданной т-кой M0(x0,y0,z0), и перпендикул.в-ром 
:A(x-x0)+B(y-y0)+C(z-z0)=0.Если выбрана с-ма координат,то ур-ние Ах+Ву+Сz+D=0(при (A,B,C,) 
(0,0,0))-общее ур-ние пл-ти. Уравнения прямой в пространстве: 1. Канонич.ур-ие прямой,зад.2-мя т-ками: 
2. Каноническое ур-ние прямой, 
,зад-ое т-кой M0(x0,y0,z0)и направляющим век-ом . 3. Параметрическое ур-ние прямой 
Взаимное расположение двух плоскостей: Пусть плоскости заданы своими общими ур-ями: 
(1) 
Вопрос о взаимном расположении этих пл-стей сводится к реш-ю 2-х лин Ур-ий с 3-мя неизв.Если коэф-ты при перем-х непропорциональны, то пл-сти пересекаются по прямой. Если коэф-ты пропорциональны, а свободные члены нет, то данные пл-сти параллельны. Если 
, то пл-сти совпадают. Взаимное расположение прямой и плоскости. Пусть в пр-ве прямая d задана точкой 
и направляющим и в-ром 
, пл-сть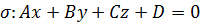 
. Тогда 1. 
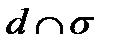, т.е. имеют общую точку; 
не параллельна 
. Для отыскания корд-т точек пересечения прямой и пл-сти решается система, сост из ур-ий прямой и пл-сти. 
2. 
3. d лежит в пл-сти 
Располож-е 2-х прямых в пр-ве. Пусть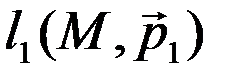 
, 
: 1. Прямые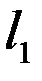 
и 
явл. скрещивающимися,если они не лежат в одной пл-ти. 2. Прямые 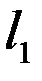и ,лежащие в одной пл-ти,пересекаются ó,когда их направлящие векторы неколлинеарны. 3. Прямые 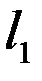и лежащие в одной пл-ти, будут параллельны, если они не имеют общих точек. 4. Прямые 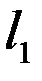и совпадают, если векторы 
, 
, 
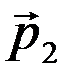попарно коллинеарны.
32. Определение ф-ии от мтрицы. Св-ва ф-ий от матриц. Интерполяционый многочлен. Спектральное разложение f(A). Пусть АÎMn(C)(мн-во квадр. м-ц над полем компл. чисел) и ф-ция f(x) – ф-ция скал. аргумента х. Требуется определить, что следует понимать под f(A). Реш-е этой з-чи изв., когда f(x)=anxn+…+a1x+a0. В этом сл. f(A)=anAn+…+a1A+a0E. Определим f(A) в общем случае. Обозн. mA(x)=(x-l1)m1(x-l2)m2…(x-lS)ms (1) - min мн-н м-цы А (l1,… lS – разл. собств. знач-ия А). Степень этого мн-на 
. Пусть 2 мн-на g(x) и h(x) таковы, что g(A)=h(A) (2). Обознач. разность d(x)=g(x)-h(x), тогда d(A)= 0 – аннулирующий мн-н для м-цы А и он делится на mA(x), тогда справ. d(x)=mA(x)q(x). Вообщем, мн-н f(x) наз. аннулирующим мн-ном для м-цы А, если f(A)=0.
SpA={ 
}. Тогда в силу (1) d(lk)=0, d’(lk)=0, …d(mk-1)(lk)=0, (k=1,s), т.е. g(lk) = h(lk), g’(lk)=h’(lk)…g(mk-1)(lk)=h(mk-1)(lk), k=1,s. Т.о. получили: если мн-ны g(x) и h(x) принимают одинаковые знач-я при x=A, то они принимают одинак.знач-я на SpA.
Пусть f(x) –нек-ая ф-я. Условимся m чисел вида f(lk),f(1)(lk)…f(mk-1)(lk) (3) наз. знач-ми ф-ии f(x) на SpA, т.е. f(SpA)={ f(lk),… f(mk-1)(lk) }(спектр м-цы – мн-во её собств. знач-й). Говорят, что ф-ция f(x) определена на SpA, если определены все знач-я f(mk-1)(lk), 
. Знач-е ф-ии f(A) опред. как знач-е нек-гомн-на g(x) при x=A, кот. приним.те же знач-я на SpA что и x. Мн-н g(x) из определения ф-ии от матриц наз. интерполяционным мн-номЛогранжа-Сильвестра.
Среди мн-нов над С, приним. те же знач-я на SpA, что и f(x) им. единств. мн-н r(x) степени <m. Это остаток от деления 
мн-на, им. те же знач. на SpA, что и f(x), на m(x), т.е. g(x)=p(x)m(x)+r(x). Мн-н r(x) будет интерполяционным мн-ном Л-С для ф-ции f(x) на SpА. Строится он так: пусть вып.(1) и (2), изв. 
. Составим дробн.-рац. ф-ю: 
и разложим её на простейшие дроби: 
(4). Умнож. (4) на знаменатель последней дроби, т.е. на 
и получ. 
(5). Тогда 
. Чтобы найти след. коэф-ты, надо найти производную от (5) и т.д. В итоге получ. r(x) и подставл. x=A, т.е. f(A)=r(A). Св-ва ф-ий от м-ц(теоремы): 1) м-ца A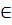 
MnC, f(x) 
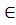C[x], l1,l2…ln – собств. знач-ия (с учетом кратностей) м-цы А, тогда f(l1),…f(ln) – собств. знач-ия м-цы f(A) 2) м-ца A 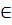MnC и f(x)-произвольная ф-я, опред. на SpA, то если l1,l2…ln – собств. знач-ия м-цы A, то f(l1),…f(ln) – собств. знач-ия м-цы f(A). Док-во: т.к. f(x) опред. на SpA, то 
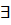интерп. мн-н r(x) такой, что r(A)=f(A) (*) и r(x) приним. те же знач-я на SpA, что и f(x), т.е. f(li)=r(li)(**). По св-ву 1) след. что если l1,l2…ln – собств. знач-ия м-цы A, то r(l1),…r(ln)- собств. знач-ия м-цы r(A), а из (*) и (**) след. f(l1),…f(ln) – собств. знач-ия м-цы f(A). 3) Если 2 м-цы A и B подобны, f(x) опред. на SpA или SpB, то собств. знач-я м-ц f(A) и f(B) совпадают и справ. f(B)=T-1f(A)T, T- невырожденная 4) Если A-блочно-диаг. м-ца, т.е. А=diag(A1,A2,…AS) и f(x) опред. на SpA, то f(A)=diag(f(A1),f(A2),…f(AS)). Т-ма о спектральном разложении: Пусть м-ца A 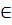MnC и для неё справ. (1), f(x)- произв. ф-я на SpA, fk(j) – значение j-ой производной при x= lk (fk(j)=f(j)(lk)), тогда сущ. незав от f м-цы zkj, что справ. разложение 
, где 
–лин. незав. и перестановочны с м-цей A и они наз. компонентными м-цами. Св-ва комп. м-ц: 1) 
2) 
3) 
4) 
