Введення поняття гомотетії і вивчення її властивостей зручно пов'язати з поняттям вектора.
Означення. Гомотетією з центром О і коефіцієнтом к≠0 називається таке перетворення площини, при якому будь-яка точка М переходить у таку точку М', що  = к
= к 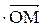 .
.
Точка М' називається образом точки М,точка М – прообразом точки М',число к – коефіцієнтом гомотетії, точка О - центром гомотетії. Якщо точка М у гомотетії переходить у точку М',то записують М ® М'. Точки М і М' називаються гомотетичними.
 Гомотетію на площині можна задати різними способами.
Гомотетію на площині можна задати різними способами.
 1. Центром О і коефіцієнтом к – за означенням. Щоб побудувати образ М' довільної точки М площини, треба від точки О відкласти вектор
1. Центром О і коефіцієнтом к – за означенням. Щоб побудувати образ М' довільної точки М площини, треба від точки О відкласти вектор  = к
= к  . Операція виконується однозначно. При цьому, якщо к > 0, то вектори
. Операція виконується однозначно. При цьому, якщо к > 0, то вектори  і
і  співнапрямлені – точки М' і М лежать з одного боку від точки О, а якщо к < 0, то
співнапрямлені – точки М' і М лежать з одного боку від точки О, а якщо к < 0, то  ¯
¯  : точки М і М' лежать по різні боки від точки О.
: точки М і М' лежать по різні боки від точки О.
2. Центром О і однією парою відповідних точок М®М'. При цьому легко знайти коефіцієнт гомотетії:  (пряма
(пряма  проходить через точку О).
проходить через точку О).
3. Коефіцієнтом к і однією парою відповідних точок М®М'. Тоді для довільної точки В,що не лежить на прямій ММ' можна побудувати її образ В',відклавши  =к
=к  . Центром гомотетії буде точка О перетину прямих ММ' і ВВ' (мал. 5.1).
. Центром гомотетії буде точка О перетину прямих ММ' і ВВ' (мал. 5.1).
4. Двома парами відповідних точок (однією парою відповідних відрізків). Справді, якщо дано дві пари відповідних точок А®А¢ і В ® В',то коефіцієнт гомотетії  (мал. 5.1, 5.2). Центром гомотетії є точка перетину прямих АА' і ВВ'. Якщо точки А, А' і В, В' лежать на одній прямій, то слід взяти довільну точку С, яка не лежить на прямій АА¢ і побудувати її образ С¢ за уже знайденим коефіцієнтом гомотетії
(мал. 5.1, 5.2). Центром гомотетії є точка перетину прямих АА' і ВВ'. Якщо точки А, А' і В, В' лежать на одній прямій, то слід взяти довільну точку С, яка не лежить на прямій АА¢ і побудувати її образ С¢ за уже знайденим коефіцієнтом гомотетії  . Центром гомотетії буде точка перетину прямих АА' і СС¢ (мал. 5.3).
. Центром гомотетії буде точка перетину прямих АА' і СС¢ (мал. 5.3).
5. Координатними формулами. Нехай гомотетія з коефіцієнтом к і центром у початку координат переводить точку М(х; у) у точку М'(х'; у'). За означенням гомотетії  = к
= к 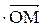 . Ця рівність рівносильна таким двом рівностям: х' = кх, у' = ky. Знаючи координати точки М і коефіцієнт гомотетії к,можна знайти координати гомотетичної їй точки М' за цими формулами.
. Ця рівність рівносильна таким двом рівностям: х' = кх, у' = ky. Знаючи координати точки М і коефіцієнт гомотетії к,можна знайти координати гомотетичної їй точки М' за цими формулами.
Властивості гомотетії
З означення гомотетії маємо такі її властивості.
1. Образом будь-якої точки в гомотетії з центром О і коефіцієнтом к є точка і при тому тільки одна.
2. Незмінною точкою площини в гомотетії є лише одна точка – центр гомотетії.
3. Незмінними прямими площини в гомотетії є всі прямі, що проходять через центр гомотетії.
4. Гомотетія з центром О і коефіцієнтом к =-1 є центральною симетрією з центром у точці О.
Справді за означенням  = -
= -  ,тобто вектори
,тобто вектори  і
і  – протилежні, точка О є серединою відрізка ММ'. Безпосередньо з властивості 4 випливають такі дві властивості.
– протилежні, точка О є серединою відрізка ММ'. Безпосередньо з властивості 4 випливають такі дві властивості.
5. Промінь, що виходить із центра гомотетії, переходить сам у себе, якщо к> 0, і в промінь, симетричний даному відносно центра гомотетії, якщо к< 0.
6. Кут із вершиною в центрі гомотетії переходить сам у себе, якщо к >0, і в кут, симетричний даному відносно вершини, якщо к< 0.
7. Кожна пряма, яка не проходить через центр гомотетії, переходить у паралельну їй пряму. Для доведення цієї властивості використаємо координатні формули гомотетії. Нехай на координатній площині пряма l задана загальним рівнянням ах + bу + с = 0, а гомотетія – формулами х'=кх, у'=ку. Тоді x=  ; y=
; y=  . Образ прямої l матиме рівняння а
. Образ прямої l матиме рівняння а  + b
+ b  + с = 0, або ах' + bу' + кс = 0. Це рівняння прямої, паралельної прямій l. Отже, гомотетичним образом прямої l є пряма l¢,їй паралельна.
+ с = 0, або ах' + bу' + кс = 0. Це рівняння прямої, паралельної прямій l. Отже, гомотетичним образом прямої l є пряма l¢,їй паралельна.
8. Гомотетія кожне коло переводить у коло, причому центри кіл гомотетичні, а відношення їх радіусів дорівнює модулю коефіцієнта гомотетії.
Це випливає з того, що при гомотетії з коефіцієнтом к всі відстані множаться на одне й те ж число  .
.
9. Гомотетичні фігури мають однакову орієнтацію (мал. 5.2).
10. Гомотетія з коефіцієнтом к= 1 є тотожним перетворенням площини. Неважко переконатися, що в гомотетії з к = 1 усі точки площини незмінні.
11. Перетворення площини, обернене до гомотетії з центром О і коефіцієнтом к, є також гомотетією з тим самим центром О і коефіцієнтом к. Справді, маємо звідси  = к
= к 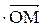 ;
;  =
= 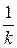
 .
.
12. Композиція гомотетій з центром О і коефіцієнтами к1 і к2 є гомотетією з тим самим центром і коефіцієнтом к = к1  к2 Справедливість властивості дістаємо з таких міркувань. Нехай
к2 Справедливість властивості дістаємо з таких міркувань. Нехай  = к1
= к1 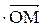 і
і  = к2
= к2  . Звідси
. Звідси  = к2
= к2  к1
к1 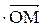 .
.
13. Композиція гомотетій із спільним центром асоціативна. Композиція гомотетій зводиться до множення коефіцієнтів гомотетії, а для чисел к1, к2, к3 операція множення асоціативна, тому й композиція гомотетій асоціативна.
Властивості 10-13є груповими властивостями гомотетії. Тому справедлива ще така властивість.
14. Сукупність усіх гомотетій площини зі спільним центром є групою.
Побудова образу фігури F при гомотетії зводиться до побудови образів точок, які визначають фігуру F. Наприклад, для побудови образу ΔАВС в гомотетії з центром О і коефіцієнтом к = -2, треба побудувати образи вершин – точки А', В', С¢:
 ;
; 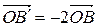 ;
;  . ΔА¢В¢С¢ гомотетичний ΔАВС.
. ΔА¢В¢С¢ гомотетичний ΔАВС.
Подібність
Означення. 6.1 Перетворення площини, при якому відстань між точками змінюється в одне й те саме число к> 0 разів, називається перетворенням подібності, або просто подібністю. Отже, якщо точки А і В переходять у точки А' і В' при подібному перетворенні, то А'В'= к  АВ (1)
АВ (1)
Число к>0 називається коефіцієнтом подібності,воно одне й те саме для всіх пар відповідних точок площини в даному перетворенні. Нагадаємо, що точки А' і В' називаються образами точок А і В,а точки А і В – прообразами точок А' і В'.
Назвемо деякі основні властивості перетворення подібності площини.
1. 3 означення випливає, що кожний рух площини можна розглядати як перетворення подібності з коефіцієнтом к = 1, тобто рух є окремим випадком перетворення подібності.
2. Перетворення подібності площини є взаємно однозначним перетворенням.
Доведення. Покажемо, що двом різним точкам А і В у перетворенні подібності відповідають також різні образи А' і В'. Припустимо протилежне: нехай А' співпадає з В', тоді довжина відрізка А'В' = 0, але А'В' = к 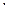 АВ,тобто 0 = к
АВ,тобто 0 = к  АВ, к ≠ 0, тому АВ =0, звідки А співпадає з В, що суперечить умові. Отже, припущення неправильне, тому А¢ ≠ В'.
АВ, к ≠ 0, тому АВ =0, звідки А співпадає з В, що суперечить умові. Отже, припущення неправильне, тому А¢ ≠ В'.
3. Будь-яке перетворення подібності має обернене перетворення, яке є також перетворенням подібності з коефіцієнтом 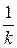 .
.
Доведення. Якщо А'В' = к  АВ,то при оберненому перетворенні АВ =
АВ,то при оберненому перетворенні АВ = 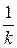 А'В'.
А'В'.
4. Композиція двох перетворень подібності з коефіцієнтами к1 і к2 є також перетворенням подібності з коефіцієнтом к = к1  кг.
кг.
Доведення. Нехай А'В' = к1  АВ і А''В'' = к2
АВ і А''В'' = к2  А'В'. Тоді А"В" = к2
А'В'. Тоді А"В" = к2  А'В' = к1
А'В' = к1  к2
к2  АВ=к
АВ=к  АВ, де к = к1
АВ, де к = к1  к2.
к2.
5. Композиція подібних перетворень сполучна. Доведення аналогічне попередньому.
З розглянутих властивостей 1-5 випливає така властивість.
6. Сукупність усіх подібних перетворень утворює групу.
7.Оскільки кожний рух є перетворенням подібності з коефіцієнтом к =1 і сукупність усіх рухів площини є групою, то група рухів є підгрупою групи подібних перетворень.
8. Колінеарність і впорядкованість точок на прямій є інваріантами перетворення подібності.
Доведення. Справді, нехай точки А, В і С – колінеарні (належать одній прямій), і точка В лежить між точками А і С. Тоді АС =АВ + ВС.
За означенням подібності для образів А', В', С¢ точок А, В, С маємо: А¢С¢=к  АС= к
АС= к  (АВ + ВС) = к
(АВ + ВС) = к  АВ + к
АВ + к  ВС = А'В' + В'С'.
ВС = А'В' + В'С'.
Із співвідношення А'С¢ = А'В' + В'С' випливає, що точки А', В', С¢ колінеарні і точка В' лежить між точками А' і С¢.
Наслідками властивості 8 є такі властивості.
9. Якщо точки неколінеарні, то їх образи в подібному перетворенні також не колінеарні.
Інваріантами перетворення називають властивості фігур, які не змінюються при даному перетворенні.
10. Перетворення подібності відображає пряму на пряму, промінь на промінь, відрізок на відрізок, кут на кут і т. д.
11. Величина кута є інваріантом подібності. Звідси: перетворення подібності відображає перпендикулярні прямі на перпендикулярні прямі; паралельність прямих є інваріантом перетворення подібності.
12. Образом кола в подібному перетворенні є коло.
Доведення. Нехай М – довільна точка кола (О; r), r = ОМ. Подібне перетворення відображає точку О на точку О', точку М – на М', при цьому О'М' = к  ОМ. Отже, образом кола (О; r) буде сукупність точок, віддалених від точки О' на відстань к
ОМ. Отже, образом кола (О; r) буде сукупність точок, віддалених від точки О' на відстань к  ОМ = к
ОМ = к  r, тобто це буде коло з центром О' і радіусом r¢= к
r, тобто це буде коло з центром О' і радіусом r¢= к  r.
r.
13. Кожна гомотетія з коефіцієнтом к є подібним перетворенням з коефіцієнтом  .
.
Доведення. Нехай А і В – дві довільні точки площини, А' і В' – їх образи в гомотетії з центром О ікоефіцієнтом к. Тоді  = к
= к 
 і
і  = к
= к 
 (мал. 5.1). Звідси
(мал. 5.1). Звідси  .
.
Отже  і
і  . Таким чином, гомотетія є окремим випадком подібності, коли пари відповідних точок належать прямим, що проходять через дану точку О – центр гомотетії.
. Таким чином, гомотетія є окремим випадком подібності, коли пари відповідних точок належать прямим, що проходять через дану точку О – центр гомотетії.
14. Група гомотетій площини зі спільним центром є підгрупою групи перетворення подібності.
Подібність фігур
Означення 6.2. Фігура F' називається подібною фігурі F,якщо існує перетворення подібності площини, в якому фігура F' є образом фігури F.
Якщо фігура F' подібна фігурі F,то записують F' ~ F. У випадку, коли відомий коефіцієнт к подібності, яка переводить фігуру F у фігуру F¢,то записують F'  F. Розглянемо деякі основні властивості подібних фігур.
F. Розглянемо деякі основні властивості подібних фігур.
1. Кожна фігура подібна сама собі з коефіцієнтом к=1. Справедливість цієї властивості випливає з того, що фігуру можна відобразити на себе, при цьому всі відстані зберігаються.
2. Якщо фігура F ' подібна фігурі F з коефіцієнтом к, то фігура F подібна фігурі F¢ з коефіцієнтом  .
.
Доведення. Якщо F'  F,то існує подібне перетворення, яке переводить фігуру F у фігуру F'. Перетворення подібності взаємно однозначне, тому дане перетворення має обернене перетворення таке, що F
F,то існує подібне перетворення, яке переводить фігуру F у фігуру F'. Перетворення подібності взаємно однозначне, тому дане перетворення має обернене перетворення таке, що F  F¢,де
F¢,де  .
.
3. Якщо фігура F' подібна фігурі F з коефіцієнтом к1, а фігура F" подібна фігурі F ' з коефіцієнтом к2, то фігура F" подібна фігурі F з коефіцієнтом к=к1  к2.
к2.
Доведення. Фігуру F" дістаємо з фігури F у результаті виконання двох подібних перетворень з коефіцієнтами к1 і к2,композицією яких є також подібне перетворення з коефіцієнтом к = к1  к2. Це й доводить властивість 3.
к2. Це й доводить властивість 3.
Теорема 6.1. Перетворення подібності площини визначається однозначно, якщо для трьох неколінеарних точок А, B, С задано як їх образи такі точки А', В', С¢, що А'В' = к  АВ, В'С' = к
АВ, В'С' = к  ВС, С'А' = к
ВС, С'А' = к  СА.
СА.






