Координатні формули паралельного перенесення 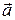 дають можливість легко довести деякі теореми про паралельне перенесення.
дають можливість легко довести деякі теореми про паралельне перенесення.
Теорема 4.2. Образом прямої в паралельному перенесенні є пряма.
Доведення. Нехай р – деяка пряма, задана рівнянням  (6)
(6)
Підставивши в це рівняння х' - х0 замість х і у' - у0 замість у, дістанемо  , або
, або  . (7)
. (7)
Звідси маємо, що множиною образів точок прямої р є також деяка пряма р'.
Наслідок 1. Відповідні в паралельному перенесенні прямі паралельні. Справді, у рівняннях (6) і (7) коефіцієнти змінних х, у і х', у' відповідно рівні, тому р║р'.
Теорема 4.3. Образом півпрямої в паралельному перенесенні є співнапрямлена з нею півпряма.
 Доведення. Нехай паралельне перенесення, задане формулами (5), переводить точку А(х 1; у1) у точку А'(х1 + а; у1 + b),точку В(х2; у2) – у точку В'(х2 + а; у2+ b). Після виконання паралельного перенесення матимемо один із двох випадків: а) точка А' не лежить на прямій АВ;б) точка А' лежить на прямій АВ (мал. 4.1).
Доведення. Нехай паралельне перенесення, задане формулами (5), переводить точку А(х 1; у1) у точку А'(х1 + а; у1 + b),точку В(х2; у2) – у точку В'(х2 + а; у2+ b). Після виконання паралельного перенесення матимемо один із двох випадків: а) точка А' не лежить на прямій АВ;б) точка А' лежить на прямій АВ (мал. 4.1).
У першому випадку за попередньою теоремою чотирикутник АА'В'В – паралелограм, у якого вершини В і В' лежать по один бік від прямої АА'. У другому випадку з того, що точка А' лежить на прямій АВ, випливає, що й точка В' лежить на цій самій прямій, бо середина (її координати) відрізка АВ збігається з серединою (її координатами) відрізка А'В,яка лежить на прямій АВ. Отже, півпрямі збігаються. Зрозуміло, що коли дві півпрямі АВ і А'В' розміщені на площині паралельно одна одній і по один бік від прямої АА' або вони збігаються, то в кожному випадку буде таке паралельне перенесення, яке одну півпряму перетворює на іншу.
Теорема 4.4. Паралельне перенесення є рухом.
Доведення. Нехай у паралельному перенесенні 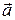 (х0, у0) точки А(х 1; у1), В(х2; у2) відображаються на точки А'(х1'; y1'), В'(х2'; y2'). Тоді
(х0, у0) точки А(х 1; у1), В(х2; у2) відображаються на точки А'(х1'; y1'), В'(х2'; y2'). Тоді  ;
;  ;
; 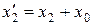 ;
;  .
.  ;
;  =
=  = =
= =  .
.
Звідси АВ = А'В',отже, паралельне перенесення є рухом.
Наслідок 2. Образом будь-якої фігури F у паралельному перенесенні є фігура F', рівна фігурі F.
Таким чином, у паралельному перенесенні кожний відрізок відображається на паралельний і рівний йому відрізок, трикутник – на рівний йому трикутник, коло – на рівне йому коло, кут – на рівний йому кут і т.д.
Назвемо, крім того, ще деякі властивості паралельного перенесення.
1. На площині в паралельному перенесенні 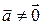 немає незмінних точок. Справді, образом кожної точки А площини є така точка А' цієї ж площини, що
немає незмінних точок. Справді, образом кожної точки А площини є така точка А' цієї ж площини, що 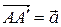 ,при
,при 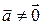 А
А  А'.
А'.
2. Незмінними прямими площини у паралельному перенесенні  є всі прямі, паралельні вектору
є всі прямі, паралельні вектору  .
.
3. Якщо точка С лежить між точками А і В, то образ С' точки С лежить між образами А' і В' точок А і В у будь-якому паралельному перенесенні.
4. Упорядкованість точок прямої є інваріантом паралельного перенесення площини.
5. Відповідні фігури в паралельному перенесенні мають однакову орієнтацію.
Розглянуті теореми і властивості дають можливість спростити побудову образів фігур у паралельному перенесенні. Так, для побудови образу відрізка досить побудувати образи його кінців, для побудови образа променя – побудувати образ його початку і однієї довільної точки, для побудови образу трикутника будуємо образи його вершин, для побудови образа кола будуємо образ його центра і тим же радіусом описуємо коло і т.д.
Загальні властивості паралельного перенесення можна використати для знаходження інваріантів конкретних фігур у даному паралельному перенесенні. Наприклад, легко переконатися, що медіана, висота, бісектриса трикутника відображається відповідно на медіану, висоту, бісектрису образу трикутника; точка перетину медіан, висот, бісектрис переходить відповідно в точку перетину медіан, висот, бісектрис і т.п.
Розглянемо нескінченну множину Р = {  ,
,  ,
,  ,...
,... 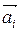 ,...
,...  ,...
,...  ,... } всіх паралельних перенесень площини, тобто множині Р належать усі можливі в площині вектори.
,... } всіх паралельних перенесень площини, тобто множині Р належать усі можливі в площині вектори.
Крім названих вище властивостей, паралельні перенесення множини Р мають ще такі властивості:
1. Композиція двох будь-яких паралельних перенесень 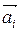 і
і  множини Р є також паралельним перенесенням
множини Р є також паралельним перенесенням  що належить множині Р. Справді, якщо Аі =
що належить множині Р. Справді, якщо Аі = 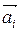 (А) і Аj =
(А) і Аj =  (Аi), то
(Аi), то  ,
, 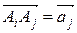 і
і  =
=  , звідси
, звідси  . Отже,
. Отже,  , де
, де  ,тобто композиція двох паралельних перенесень
,тобто композиція двох паралельних перенесень 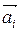 і
і  множини Р – це також паралельне перенесення на вектор
множини Р – це також паралельне перенесення на вектор  ,що є сумою векторів
,що є сумою векторів 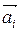 і
і  . Вектор
. Вектор  ,як і всі інші вектори площини, належить множині Р.
,як і всі інші вектори площини, належить множині Р.
2. Композиція паралельних перенесень множини Р асоціативна.
Нехай маємо три паралельні перенесення А1 =  (А), А2 =
(А), А2 =  (А1), А3 =
(А1), А3 = 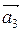 (А2). Тоді, виконуючи спочатку паралельні перенесення
(А2). Тоді, виконуючи спочатку паралельні перенесення  і
і  , дістанемо А2 =
, дістанемо А2 =  , і після виконання
, і після виконання 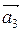 А3 =
А3 =  =
=  ,(8)
,(8)
де 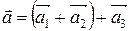 . м Якщо ж виконати спочатку
. м Якщо ж виконати спочатку  , а потім композицію
, а потім композицію  , то матимемо А3 =
, то матимемо А3 = 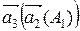 =
= 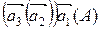 =
=  , (9)
, (9)
де  .
.
З (8) і (9) маємо  , тобто
, тобто 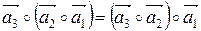 .
.
3. Паралельне перенесення на вектор  залишає незмінними всі точки площини. Таке перетворення площини називається тотожним перетворенням. Отже, серед паралельних перенесень множини Р є тотожне перетворення, яке визначається нуль-вектором.
залишає незмінними всі точки площини. Таке перетворення площини називається тотожним перетворенням. Отже, серед паралельних перенесень множини Р є тотожне перетворення, яке визначається нуль-вектором.
4. Перетворення, обернене до будь-якого паралельного перенесення 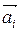 з множини Р,є також паралельним перенесенням на вектор, протилежний вектору
з множини Р,є також паралельним перенесенням на вектор, протилежний вектору 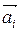 . Справді, нехай
. Справді, нехай 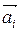 – паралельне перенесення і А – довільна точка площини. Тоді А' =
– паралельне перенесення і А – довільна точка площини. Тоді А' = 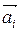 (А) і
(А) і 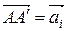 . Обернене до
. Обернене до 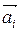 перетворення ставить у відповідність точці А' таку точку А,яка була її прообразом у перетворенні
перетворення ставить у відповідність точці А' таку точку А,яка була її прообразом у перетворенні 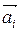 тобто
тобто 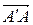 – обернене перетворення до
– обернене перетворення до 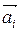 . Отже,
. Отже,  .
.
Названі чотири властивості є груповими властивостями множини перетворень, вони мають місце в множині Р. Таким чином, теорему доведено.
Теорема 4.5. Множина Р всіх паралельних перенесень площини є групою.
Теорема 4.6. Композиція двох осьових симетрій з паралельними осями є паралельним перенесенням.
Теорема 4.7. Композиція повороту навколо точки і паралельного перенесення є поворотом навколо точки.
Теорема 5.8. Композиція двох поворотів навколо різних центрів є поворотом або паралельним перенесенням.
Гомотетія






