З означення симетричних точок, фігур і перетворення симетрії відносно прямої l площини випливає ряд властивостей, які використовуються при застосуванні осьової симетрії.
1. Для кожної прямої l площини існує симетрія Sl відносно цієї прямої.
2. Незмінними (подвійними) точками осьової симетрії є всі точки осі симетрії l. Інших подвійних точок осьова симетрія на площині не має. Отже, вісь симетрії – це множина незмінних точок площини в осьовій симетрії.
3. Незмінною прямою в осьовій симетрії є, по-перше, вісь симетрії і, по-друге, кожна пряма, перпендикулярна осі симетрії. Кожна точка осі симетрії як незмінної прямої незмінна. Таку пряму, кожна точка якої незмінна в якомусь перетворенні, називають точково інваріантною. На відміну від осі симетрії всі інші незмінні прямі – перпендикулярні до осі симетрії, мають тільки по одній незмінній точці, якою є точка перетину цих прямих з віссю симетрії. Інші точки цих незмінних прямих не подвійні, кожна з них має свій образ, що не збігається з прообразом.
4. Осьова симетрія має властивість взаємності, тобто якщо А'= Sl(А), то і A = Sl(А'). Точки А і А' називають взаємно симетричними в Sl. Перетворення площини, при якому образом кожної точки є прообраз (тобто коли А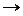 
А', то й А' 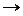А), називається інволюційним. Отже, перетворення площини в симетрії відносно прямої є інволюційним перетворенням.
5. Якщо пряма а і її образ а' в осьовій симетрії Sl перетинаються в якійсь точці А0, то ця точка перетину належить осі симетрії l. Справді, образ точки А0 прямої а повинен належати як прямій a'=Sl(a), так і прямій, проведеній через А0 перпендикулярно до l. Оскільки А0 = а 
а', то перпендикуляр, проведений до l через А0, не може перетнути а' в іншій точці, відмінній від А0, бо він перетинає пряму а' в точці А0. Отже, А0 є l.
6. Якщо пряма а перетинає вісь симетрії l в якійсь точці А0, то через точку А0 пройде і пряма а' – образ прямої а в осьовій симетрії Sl.
7. Будь-які дві точки площини мають лише одну вісь симетрії.
8. Для будь-яких півпрямих АВ і АС існує така симетрія Sl, при якій кожна з них переходить у другу відносно прямої l; пряма l є бісектрисою кута ВАС.
9. Фігури, що мають єдину вісь симетрії, поділяються нею на дві асиметричні частини протилежної орієнтації, які називаються енантіоморфами. Лівий і правий енантіоморфи не можна сумістити ніяким рухом у площині, відмінним від осьової симетрії, їх можна сумістити, якщо виконати поворот у тривимірному просторі навколо осі симетрії.
Теорема 2.1. Осьова симетрія на площині є рухом.
Для доведення теореми досить довести, що відстань між точками А і В дорівнює відстані між їх образами А' і В' в симетрії відносно прямої l. З цією метою використаємо координатний метод у системі (О,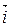 
, 
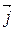),вісь ОХ якої збігається з віссю симетрії.
Дано: А'(х'; у') = Sl (А(х; у)), В'(х'1; у'1) = Sl (В(х1; y 1 )). Довести: А'В' = АВ.
Доведення. А'В' = 
. Врахувавши формули залежності між координатами образа і прообраза, які в даному випадку мають вигляд: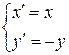 
і 
, знайдемо, що А'В'= = 
= 
= = АВ.
Цю теорему можна довести на основі рівності трикутників без використання системи координат (виконати самостійно).
Наведемо ще деякі властивості осьової симетрії, які є наслідком з доведеної теореми 2.1.
Наслідок 1. Фігури, симетричні відносно прямої, рівні, але мають протилежну орієнтацію (мал. 2.2).
Наслідок 2. В осьовій симетрії пряма відображається на пряму, промінь - на промінь.
Наслідок 3. Упорядкованість точок прямої є інваріантом осьової симетрії.
Наслідок 4. Симетричні прямі або перетинаються на осі симетрії, або паралельні їй.
Наслідок 5. Паралельність прямих є інваріантом осьової симетрії.
Наслідок 6. Точки осі симетрії рівновіддалені від будь-якої пари симетричних точок.
Наслідок 7. Для будь-яких двох прямих, що перетинаються, можна побудувати дві осі симетрії – це бісектриси кутів, утворених прямими.
Наслідок 8. Будь-які дві різні паралельні прямі мають одну вісь симетрії – це множина точок, рівновіддалених від даних паралельних прямих.
Наслідок 9. Об'єднання двох фігур, які мають спільну вісь симетрії, симетричне відносно цієї ж осі.
Наслідок 10. Переріз двох фігур, які мають спільну вісь симетрії, симетричний відносно тієї ж осі.
Наслідок 11. Колінеарність точок зберігається при осьовій симетрії.
Наслідок 12. Симетричні прямі утворюють з віссю симетрії рівні кути.
Теорема 2.2. Композиція двох осьових симетрій із взаємно перпендикулярними осями є центральною симетрією, центр якої збігається з точкою перетину осей симетрії.
Доведення. Нехай а, b - осі симетрії, а ^ b; О = а b (мал. 2.3). Візьмемо довільну точку А і побудуємо їй симетричну відносно прямої а точку А1, при цьому ОА=ОА1, Ð1=Ð2.(1)
Побудуємо далі точку А2,симетричну точці А1 відносно прямої b,при цьому ОА1=ОА2, Ð3=Ð4. (2)
Враховуючи рівності (1) і (2), а також те, що Ð2+Ð3= 90°, дістанемо Ð ОА2 =ОА, ÐАОА2 = Ð1+Ð2+ +Ð3+Ð4 = 180°.
Отже, точка О лежить на відрізку АА2 і ділить його навпіл, тобто точка О є центром симетрії відрізка АА2, точка А2 = Z0 (А). Цим доведено, що коли а ^ b,то Sа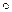 
Sb = Z0,де O = а b.
Наслідок 1. Множина всіх осьових симетрій на площині не утворює групи перетворень площини.
Наслідок 2. Композиція двох осьових симетрій із взаємно перпендикулярними осями симетрії комутативна. Справді,
1) ( А1=Sа(А), А2=Sb(A1)) Þ Sb 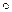Sa = Z0;
2) ( B1=Sb(А), B2=Sa(B1)) Þ Sa 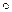Sb = Z0;
3) А2 =В2 Þ Sb 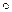Sa = Sa 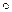Sb.
Теорема 2.3. Композиція трьох осьових симетрій відносно трьох прямих а, b і с, які мають спільну точку О є осьовою симетрією з віссю d,яка проходить через точку О.
Доведення. У композиції Sc 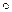Sb 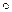Sa, де а, b, с – дані прямі, які мають спільну точку О, усі три компоненти – осьові симетрії, кожна з яких змінює орієнтацію фігури на протилежну. У результаті композиції трьох осьових симетрій дістаємо фігуру, орієнтація якої буде протилежною орієнтації даної фігури. Тому результатом композиції трьох осьових симетрій може бути або осьова симетрія, або ковзна симетрія. Оскільки точка О при цьому залишається незмінною, то композицією трьох осьових симетрій буде осьова симетрія, вісь якої d повинна проходити через точку О.
Для побудови осі d результуючої симетрії, зручно вибрати прообразом точку А довільно на прямій а. Тоді А = Sа(А), і, якщо А'=Sb(А) і А"= Sс(А), то шукана вісь d є серединним перпендикуляром відрізка АА".
Поворот
Означення 3.1. Поворотом площини навколо заданої точки О на даний кут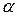 
називається таке перетворення, при якому кожній точці А площини, відмінній від точки О, ставиться у відповідність така точка А' цієї самої площини, що: 1) ОА = ОА', 2) кут АОА' дорівнює даному куту 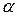і однаково з ним орієнтований.
Точка О при цьому називається центром повороту, а кут 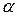- кутом повороту.
Поворот площини навколо точки О на кут 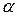позначатимемо символом 
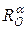(від латинського слова Rotation). Якщо точка А' є образом точки А у повороті навколо точки О на кут 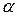, то це записують так: А'= 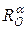(А) або 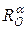: А 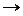А'. Із запису А'В'= 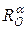(АВ) маємо, що пряма А'В' є образом прямої АВ при повороті .
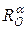Із наведеного означення випливає, що поворот навколо точки повністю визначається заданням центра повороту і орієнтованого кута повороту. Крім того, поворот може бути заданий центром повороту і парою відповідних точок або двома парами відповідних точок (парою відповідних відрізків).
Кут повороту є напрямленою величиною, тому числове значення кута повороту може бути як додатним, так і від'ємним. Додатним вважають напрям повороту проти руху стрілки годинника. Кут повороту а може мати значення в межах -180° < 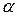< 180°.
Звертаємо увагу на те, що в науковій літературі, крім терміну «поворот» навколо точки, у тому самому розумінні вживають термін «обертання». Відомо, що кожна точка площини повертається в попереднє положення при обертанні на 360°, на 2•360° і т.д., на п 
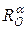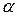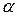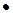360°, де п – будь-яке ціле число. Тому поворот дістанемо не лише обертанням на кут , а й на кут + п 360°, де п – будь-яке ціле число.
Кожна геометрична фігура – це певна множина точок. Для побудови образу фігури в даному повороті 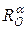треба вміти будувати образи точок. Якщо задано поворот 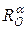,то для побудови образу А' довільної точки А площини треба: 1) сполучити А з центром повороту О; 2) побудувати кут АОА', рівний куту 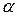і однаково з ним орієнтований; 3) на промені ОА' відкласти відрізок ОА' = ОА.
Теорема 3.1. Будь-який поворот площини навколо точки можна подати у вигляді композиції двох осьових симетрій площини.
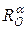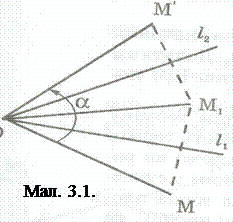
Доведення. Нехай дано поворот , який відображає довільно взяту точку М на точку М': М' = 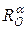(М). Проведемо через центр О повороту довільний промінь l1 (мал. 3.1.) і знайдемо образ M1, точки М у симетрії відносно променя l1: M1= S 
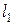(M). Далі побудуємо вісь симетрії l2 точок М1 і М' – це буде серединний перпендикуляр відрізка М1М'. Вісь 12 пройде через точку О (трикутник М1ОМ' – рівнобедрений, ОМ1=ОМ'). Осьова симетрія поставить у відповідність точці М1 точку М': М'=S 
(M1). Отже, точку М' дістаємо з точки М композицією двох осьових симетрій S 
S 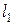. Кут повороту 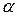у два рази більший кута між осями симетрії l1 і 12: Ð(l1, l2)= 
. Справді, за властивостями осьової симетрії Ð1=Ð2 і Ð3=Ð4. Звідси Ð(l1, l2)= =Ð2+Ð3= . Має місце й обернене твердження.
Теорема 3.2. Композиція двох осьових симетрій з непаралельними осями l1 і l2 є поворотом навколо точки перетину осей симетрії на кут, рівний подвійному куту між осями симетрії.
