Векторним добутком векторів 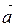 та
та  називається вектор
називається вектор 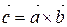 , який задовольняє умови:
, який задовольняє умови:
– напрям вектора  такий, що він перпендикулярний до площини, в якій лежать вектори
такий, що він перпендикулярний до площини, в якій лежать вектори 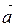 та
та  , тобто
, тобто  ;
;
– вектор  утворює з векторами
утворює з векторами 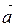 та
та  так звану праву трійку векторів, тобто вектор
так звану праву трійку векторів, тобто вектор  проведений так, що спостерігач бачить з його кінця найкоротший шлях від вектора
проведений так, що спостерігач бачить з його кінця найкоротший шлях від вектора 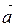 до вектора
до вектора  проти годинникової стрілки (рис. 2.9);
проти годинникової стрілки (рис. 2.9);
– довжина вектора  визначається за формулою (2.20)
визначається за формулою (2.20)
 . .
| (2.20) |

| |
| Рис. 2.9 |
Геометричний зміст векторного добутку: модуль векторного добутку векторів дорівнює площі паралелограма, сторонами якого є дані вектори.
Властивості векторного добутку векторів:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  , якщо
, якщо  ;
;
6) добутки ортів  ,
,  ,
,  ,
,  ,
,  ,
, 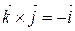 ,
,  .
.
Якщо вектори задані в координатній формі  та
та  , то векторний добуток векторів можна записати у вигляді (2.21)
, то векторний добуток векторів можна записати у вигляді (2.21)
 . .
| (2.21) |
Основні задачі, які розв’язуються з використанням векторного добутку векторів:
1) площа паралелограма, побудованого на векторах 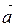 та
та 
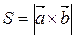 ; ;
| (2.22) |
2) площа трикутника, побудованого на векторах 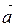 та
та 
 ; ;
| (2.23) |
3) висота паралелограма
 ; ;
| (2.24) |
4) висота трикутника
 . .
| (2.25) |
Змішаний добуток векторів
Змішаним (або векторно-скалярним) добутком трьох векторів 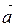 ,
,  та
та  називається сукупність операцій:
називається сукупність операцій:
 . .
| (2.26) |
Змішаний добуток трьох векторів – це скалярний добуток одного з цих векторів на векторний добуток двох інших векторів.
Геометричний зміст змішаного добутку: модуль змішаного добутку трьох векторів дорівнює об’єму паралелепіпеда (рис. 2.11), побудованого на цих векторах, як на його ребрах.

| |
| Рис. 2.11 | |

| (2.27) |
Якщо вектори задані в координатній формі  ,
,  та
та  , то змішаний добуток векторів можна записати у вигляді
, то змішаний добуток векторів можна записати у вигляді
 . .
| (2.28) |
Властивості змішаного добутку векторів:
1) 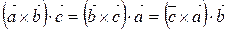 ;
;
2)  ;
;
3)  ;
;
4)  , якщо вектори
, якщо вектори 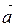 ,
,  та
та  компланарні;
компланарні;
5)  , якщо вектори
, якщо вектори 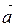 ,
,  та
та  утворюють праву трійку векторів;
утворюють праву трійку векторів;
6)  , якщо вектори
, якщо вектори 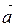 ,
,  та
та  утворюють ліву трійку векторів.
утворюють ліву трійку векторів.
Основні задачі, які розв’язуються з використанням змішаного добутку векторів:
1) об’єм паралелепіпеда, побудованого на векторах 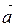 ,
,  та
та 
 ; ;
| (2.29) |
2) об’єм піраміди, побудованої на векторах 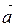 ,
,  та
та 
 ; ;
| (2.30) |
3) висота паралелепіпеда
 ; ;
| (2.31) |
4) висота піраміди
 . .
| (2.32) |
Індивідуальне завдання за темою „Векторна алгебра”
Дано координати точок  . Необхідно:
. Необхідно:
1. Знайти модуль та напрямок вектора  у просторі.
у просторі.
2. Знайти кут між векторами  та
та  .
.
3. Знайти проекцію вектора  на напрям вектора
на напрям вектора  .
.
4. Знайти вектор  , перпендикулярний до вектора
, перпендикулярний до вектора  і до
і до  .
.
5. Обчислити площу трикутника АВС.
6. Знайти висоту паралелограма, побудованого на векторах  і
і  .
.
7. Обчислити об’єм піраміди  .
.
8. Перевірити, чи колінеарні вектори  і
і  .
.
9. Перевірити, чи ортогональні вектори  і
і  .
.
10. Перевірити, чи належать точки 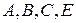 до однієї площини.
до однієї площини.
| Варіант 1 |  (0; -1; 2) (0; -1; 2)
|  (1; 2; 1) (1; 2; 1)
|  (-3; 2; 1) (-3; 2; 1)
|  (0; 0; -1) (0; 0; -1)
|  (2; 6; -3) (2; 6; -3)
|
| Варіант 2 |  (-1; 3; 0) (-1; 3; 0)
|  (2; 1; -1) (2; 1; -1)
|  (3; -1; 2) (3; -1; 2)
|  (1; -1; 3) (1; -1; 3)
|  (5; 2; 2) (5; 2; 2)
|
| Варіант 3 |  (0; 3; 1) (0; 3; 1)
|  (2; -1; 3) (2; -1; 3)
|  (0; 2; 1) (0; 2; 1)
|  (0; 1; 3) (0; 1; 3)
|  (1; -1;-4) (1; -1;-4)
|
| Варіант 4 |  (-1; 2; 3) (-1; 2; 3)
|  (-1; 3; 0) (-1; 3; 0)
|  (0; -1; 2) (0; -1; 2)
|  (-2;1;-1) (-2;1;-1)
|  (5; 2; 3) (5; 2; 3)
|
| Варіант 5 |  (2; -2; 0) (2; -2; 0)
|  (-2; -1;3) (-2; -1;3)
|  (1; -2; 0) (1; -2; 0)
|  (-1; 0; 1) (-1; 0; 1)
|  (7;-2; -5) (7;-2; -5)
|
| Варіант 6 |  (-2; 0;-1) (-2; 0;-1)
|  (1; -2; 0) (1; -2; 0)
|  (0; 1; 1) (0; 1; 1)
|  (2; 0; -3) (2; 0; -3)
|  (-1; 1; 4) (-1; 1; 4)
|
| Варіант 7 |  (0; 1; -2) (0; 1; -2)
|  (2; 2; -1) (2; 2; -1)
|  (-1; -1;0) (-1; -1;0)
|  (-1;-1;0) (-1;-1;0)
|  (5; 2; 3) (5; 2; 3)
|
| Варіант 8 |  (3; 1; -1) (3; 1; -1)
|  (2; -1; 0) (2; -1; 0)
|  (2; 1; 0) (2; 1; 0)
|  (2; 1; 3) (2; 1; 3)
|  (4; 0; 0) (4; 0; 0)
|
| Варіант 9 |  (3; 2; 0) (3; 2; 0)
|  (1; -1; 1) (1; -1; 1)
|  (2; 0; -1) (2; 0; -1)
|  (2; 0; -1) (2; 0; -1)
|  (6; 6; -3) (6; 6; -3)
|
| Варіант 10 |  (0; -3;-1) (0; -3;-1)
|  (1; 0; -2) (1; 0; -2)
|  (-1; 0; 2) (-1; 0; 2)
|  (0; 0; 1) (0; 0; 1)
|  (-1; 1; 5) (-1; 1; 5)
|
| Варіант 11 |  (2; 1; -2) (2; 1; -2)
|  (1; 2; 3) (1; 2; 3)
|  (0; 3; 1) (0; 3; 1)
|  (-1;-2;-3) (-1;-2;-3)
|  (2;-5;-18) (2;-5;-18)
|
| Варіант 12 |  (0; 3; -2) (0; 3; -2)
|  (1; -2; 1) (1; -2; 1)
|  (-1; 0; 3) (-1; 0; 3)
|  (1; -2; 0) (1; -2; 0)
|  (-4; 0; 4) (-4; 0; 4)
|
| Варіант 13 |  (2; -1; 3) (2; -1; 3)
|  (0; 1; -1) (0; 1; -1)
|  (-2; 3; 1) (-2; 3; 1)
|  (0; -1; 0) (0; -1; 0)
|  (1; -2; 2) (1; -2; 2)
|
| Варіант 14 |  (0; 2; -1) (0; 2; -1)
|  (1; 3; -1) (1; 3; -1)
|  (-2; 1; 0) (-2; 1; 0)
|  (3; 0; 1) (3; 0; 1)
|  (0; -1; 3) (0; -1; 3)
|
| Варіант 15 |  (1; -1; 2) (1; -1; 2)
|  (3; 1; -2) (3; 1; -2)
|  (0; 1; -1) (0; 1; -1)
|  (2; 3; 0) (2; 3; 0)
|  (1; 2; 2) (1; 2; 2)
|
| Варіант 16 |  (1; 0; 2) (1; 0; 2)
|  (-1; 2; 3) (-1; 2; 3)
|  (1; 0; -3) (1; 0; -3)
|  (2; 1; -1) (2; 1; -1)
|  (5; 3; -1) (5; 3; -1)
|
| Варіант 17 |  (1;-3;-2) (1;-3;-2)
|  (0; -2; 1) (0; -2; 1)
|  (2; -3; 1) (2; -3; 1)
|  (-1; 0; 0) (-1; 0; 0)
|  (-4; 3; 9) (-4; 3; 9)
|
| Варіант 18 |  (1; -2; 2) (1; -2; 2)
|  (0; 1; 3) (0; 1; 3)
|  (2; 1; -1) (2; 1; -1)
|  (-3; 1; 0) (-3; 1; 0)
|  (6; 2; 0) (6; 2; 0)
|
| Варіант 19 |  (2; -1; 0) (2; -1; 0)
|  (0; 1; 1) (0; 1; 1)
|  (-2; 0; 1) (-2; 0; 1)
|  (-1;-1;-1) (-1;-1;-1)
|  (0; -2; 0) (0; -2; 0)
|
| Варіант 20 |  (-3; 0; 1) (-3; 0; 1)
|  (1;-2; -1) (1;-2; -1)
|  (0; 3; 1) (0; 3; 1)
|  (-2; 1; 0) (-2; 1; 0)
|  (1; 4; 2) (1; 4; 2)
|
| Варіант 21 |  (-3;1;-1) (-3;1;-1)
|  (0; 2; 1) (0; 2; 1)
|  (-1; 3; 2) (-1; 3; 2)
|  (2; -2; 2) (2; -2; 2)
|  (-1;-3;0) (-1;-3;0)
|
| Варіант 22 |  (-1;-2;-3) (-1;-2;-3)
|  (2; 1; 0) (2; 1; 0)
|  (0; 1; -1) (0; 1; -1)
|  (-3;1;-1) (-3;1;-1)
|  (-1; 1; 0) (-1; 1; 0)
|
| Варіант 23 |  (-1; 0; 0) (-1; 0; 0)
|  (1; 2; -3) (1; 2; -3)
|  (2; 0; -1) (2; 0; -1)
|  (1; 3; -1) (1; 3; -1)
|  (-1; 1; 2) (-1; 1; 2)
|
| Варіант 24 |  (0; 0; -2) (0; 0; -2)
|  (2; 1; -3) (2; 1; -3)
|  (0; 1; -2) (0; 1; -2)
|  (-2;-1;0) (-2;-1;0)
|  (1; 4; 3) (1; 4; 3)
|
| Варіант 25 |  (-2;-1;-3) (-2;-1;-3)
|  (-3; 1; 0) (-3; 1; 0)
|  (2; 1; -1) (2; 1; -1)
|  (0; 1; 3) (0; 1; 3)
|  (-2; 5; 9) (-2; 5; 9)
|
| Варіант 26 |  (0; 1; -4) (0; 1; -4)
|  (2; 2; -3) (2; 2; -3)
|  (-1;3; -1) (-1;3; -1)
|  (1; 1; 1) (1; 1; 1)
|  (-2; 4; 0) (-2; 4; 0)
|
| Варіант 27 |  (-3;0;1) (-3;0;1)
|  (-2; 1; 3) (-2; 1; 3)
|  (0;-1; -2) (0;-1; -2)
|  (-1;-2;-5) (-1;-2;-5)
|  (1; 0; 3) (1; 0; 3)
|
| Варіант 28 |  (3; 0; -2) (3; 0; -2)
|  (2; 1; -3) (2; 1; -3)
|  (-1; 0; 2) (-1; 0; 2)
|  (2;-1;-1) (2;-1;-1)
|  (2; 0; -1) (2; 0; -1)
|
| Варіант 29 |  (-4; 0; 3) (-4; 0; 3)
|  (-3; 1; 2) (-3; 1; 2)
|  (-1; 0; 2) (-1; 0; 2)
|  (0; -3; 1) (0; -3; 1)
|  (-3; 0; 4) (-3; 0; 4)
|
| Варіант 30 |  (2; 2; 2) (2; 2; 2)
|  (3; 2; 0) (3; 2; 0)
|  (-1; 3;-1) (-1; 3;-1)
|  (-2;-1;3) (-2;-1;3)
|  (-1;-1;-1) (-1;-1;-1)
|






