За допомогою систем лінійних алгебраїчних рівнянь моделюється переважна більшість практичних задач з економіки.
 ,
| (1.14) |
де 
– коефіцієнти рівняння; 
– невідомі рівняння; 
– вільні члени рівняння.
Розв’язком системи лінійних алгебраїчних рівнянь називають таку сукупність чисел, яка перетворює всі рівняння (1.14) на числові тотожності.
Якщо права частина (1.14) дорівнює нулю 
, то систему рівнянь називають однорідною, або неоднорідною, якщо 
.
Система рівнянь (1.14) називається сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо не має жодного розв’язку.
Складемо визначник третього порядку з коефіцієнтів систем – головний визначник системи:
 .
| (1.15) |
Можливі наступні випадки розв’язку системи лінійних алгебраїчних рівнянь:
1) 
, тоді система (1.14) має єдиний розв’язок, який можна знайти або за формулами Крамера, або методом Гаусса, або матричним способом;
2) 
, тоді система (1.14) або несумісна, або має безліч розв’язків.
Розв’язування системи лінійних алгебраїчних рівнянь за формулами Крамера: необхідно скласти три визначники третього порядку з головного визначника (1.15) шляхом перестановки замість 1, 2, 3–го стовпця стовпець вільних членів – це додаткові визначники
 .
| (1.16) |
За формулами Крамера розв’язок системи рівнянь (1.14) має такий вигляд:
 .
| (1.17) |
Метод Гаусса розв’язування системи лінійних алгебраїчних рівнянь: метод послідовних вилучень невідомих, запропонований Гауссом можна розглянути на прикладі системи (1.14), поділивши перше рівняння на 
, друге – на 
, третє – на 
, матимемо:
 ,
| (1.18) |
де 
. Віднявши від другого і третього рівняння перше, дістанемо
 ,
| (1.19) |
де 
.
Поділивши перше рівняння на 
, а друге – на 
, отримаємо
 .
| (1.20) |
Віднявши перше рівняння від другого, дістанемо
 ,
| (1.21) |
звідки
 .
| (1.22) |
Тепер можна знайти 
та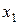 
.
Матричний метод розв’язування системи лінійних алгебраїчних рівнянь: якщо систему (1.14) записати в матричній формі
 .
| (1.23) |
де 
– матриця коефіцієнтів системи;
– матриця невідомих;
– матриця вільних членів.
 .
| (1.24) |
Помножимо (1.23) на обернену матрицю 
. Оскільки 
, то дістанемо матричний спосіб розв’язування систем:
 .
| (1.25) |
Розглянемо однорідну систему рівнянь:
 .
| (1.26) |
Складемо головний визначник системи. При розв’язанні системи (1.26) можуть бути випадки:
1) , тоді система (1.26) має єдиний нульовий розв’язок, тобто 
;
2) , тоді система (1.26) може мати безліч ненульових розв’язків, тобто буде неозначеною. У цьому випадку одне з рівнянь системи є лінійною комбінацією двох інших і може бути відкинуте. Тоді система буде складатися з двох рівнянь з трьома невідомими і матиме, наприклад, вигляд:
 .
| (1.27) |
Нехай із трьох визначників другого порядку цієї системи хоча б один не дорівнює нулеві, наприклад, визначник із коефіцієнтів при невідомих 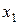та :
 .
| (1.28) |
Тоді система (1.27) є невизначеною і має безліч розв’язків, які знаходять за формулами:
 .
| (1.29) |
де 
, 
, 
– довільне дійсне число.
Може бути випадок, коли усі три визначники системи (1.27) дорівнюють нулю. Тоді одне з рівнянь системи є наслідком іншого і може бути відкинуто. Залишається одне рівняння системи (1.27), наприклад, перше. Якщо, наприклад, , то система має розв’язок, що знаходять за формулами:
 ,
| (1.30) |
де 
– довільні дійсні числа.
Індивідуальне завдання за темою „Лінійна алгебра”
Завдання І. Задані матриці 
. Необхідно:
1. Знайти величину визначника матриці (
) трьома способами:
а) використавши правило трикутника (правило Саррюса);
б) розклавши визначник за елементами того рядка, який містить нуль;
в) одержавши два нулі в будь-якому рядку і розклавши визначник по елементах цього рядка.
2. Знайти матрицю , якщо 
, де 
– одинична матриця третього порядку.
3. Знайти два можливі добутки, утворені з матриць .
4. Знайти матрицю , обернену до матриці .
| Варіант 1 | 
| 
| 
|
| Варіант 2 | 
| 
| 
|
| Варіант 3 | 
| 
| 
|
| Варіант 4 | 
| 
| 
|
| Варіант 5 | 
| 
| 
|
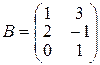
| Варіант 6 | 
| 
| 
|
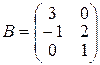
| Варіант 7 |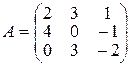 
| 
| 
|
| Варіант 8 | 
| 
| 
|
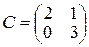
| Варіант 9 | 
| 
| 
|
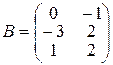
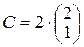
| Варіант 10 | 
| 
| 
|
| Варіант 11 | 
| 
| 
|
| Варіант 12 | 
| 
| 
|
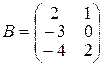
| Варіант 13 | 
| 
| 
|
| Варіант 14 | 
| 
| 
|
| Варіант 15 | 
| 
| 
|
| Варіант 16 |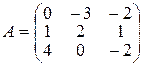 
| 
|
|
| Варіант 17 |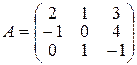 
| 
| 
|
| Варіант 18 | 
| 
|
|
| Варіант 19 | 
| 
| 
|
| Варіант 20 | 
| 
| 
|
| Варіант 21 |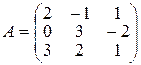 
| 
| 
|
| Варіант 22 | 
| 
| 
|
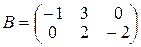
| Варіант 23 | 
| 
| 
|
| Варіант 24 | 
| 
| 
|
| Варіант 25 | 
| 
| 
|
| Варіант 26 |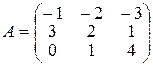 
| 
| 
|
| Варіант 27 | 
| 
| 
|
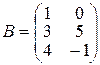
| Варіант 28 | 
| 
| 
|
| Варіант 29 | 
| 
| 
|
| Варіант 30 | 
| 
| 
|
Завдання ІІ. Знайти величину визначника четвертого порядку, скориставшись його властивостями та одержавши три нулі в будь-якому рядку.
Варіант 1
| Варіант 2
| Варіант 3
|
Варіант 4
| Варіант 5
| Варіант 6
|
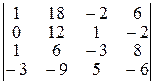
Варіант 7
| Варіант 8
| Варіант 9
|
Варіант 10
| Варіант 11
| Варіант 12
|
Варіант 13
| Варіант 14
| Варіант 15
|
Варіант 16
| Варіант 17
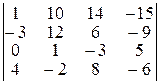
| Варіант 18
|
Варіант 19
| Варіант 20
| Варіант 21
|
Варіант 22
| Варіант 23
| Варіант 24
|
Варіант 25
| Варіант 26
| Варіант 27
|
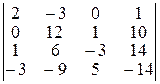
Варіант 28
| Варіант 29
| Варіант 30
|
Завдання ІІІ. Розв’язати систему лінійних алгебраїчних рівнянь трьома способами:
а) за формулами Крамера;
б) методом Гаусса;
в) методом оберненої матриці.
Варіант 1
| Варіант 2
| Варіант 3
|
Варіант 4
| Варіант 5
| Варіант 6
|
Варіант 7
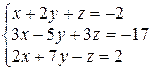
| Варіант 8
| Варіант 9
|
Варіант 10
| Варіант 11
| Варіант 12
|
Варіант 13
| Варіант 14
| Варіант 15
|
Варіант 16
| Варіант 17
| Варіант 18
|
Варіант 19
| Варіант 20
| Варіант 21
|
Варіант 22
| Варіант 23
| Варіант 24
|
Варіант 25
| Варіант 26
| Варіант 27
|
Варіант 28
| Варіант 29
| Варіант 30
|
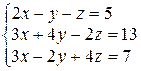
