Основные формы задач линейного программирования

Получаемая на этапе структурирования линейная оптимизационная модель может быть представлена в различных формах задач линейного программирования:

Общей

Стандартной

Канони ческой.

Общая задача линейного программирования. (ЗЛП)

Требуется найти значения переменных х₁,х₂,…х_n удовлетворяющих ограничениям вида

(1)

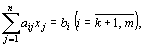
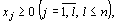
где - постоянные числа и .

И обращающих в минимум функцию

(2)

Функция 2 называется целевой функцией ЗЛП

Определение: Упорядоченный набор х₁^*,х₂^*,…х_n^* называется опорным решением задачи линейного программирования (1)(2) если он удовлетворяет системе ограничений (1)

Упорядоченный набор х₁^*,х₂^*,…х_n^* называется оптимальным решением задачи линейного программирования (1)(2) если он удовлетворяет системе ограничений (1) и обращает в минимум целевую функцию (2)

Стандартная ЗЛП

Требуется найти значения переменных х₁,х₂,…х_n удовлетворяющих ограничениям вида

(3)

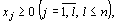
И обращающих в минимум функцию

(4)

Каноническая ЗЛП

Требуется найти значения переменных х₁,х₂,…х_n удовлетворяющих ограничениям вида

 

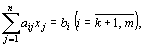(5)

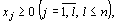
где - постоянные числа и .

И обращающих в минимум функцию

(6)

 

Замечания все 3 формы ЗЛП эквивалентны минимум целевой функции во всех з-х задачах совпадает.

Замечание к каноническому можно отнести любую задачу ЛП

Если целевая функция →max, то Ž = -Z будет минимизироваться

Кроме того от любого ограничения неравенства можно перейти к ограничению равенства путем введения фиктивной неотрицательной переменной

3х₁+7х₂≤45

Х₃≥0

3х₁+7х₂+ х₃≤45

 

Вопрос №8

Графический метод решения задач линейного программирования.

Рассмотрим ЗЛП, зпданную в стандартной форме следущего вида:

с₁х₁+с₂х₂ →max (1)

a₁₁x₁+a₁₂x₂≤ b₁

a₂₁x₁+a₂₂x₂≤ b₂ (2)

a_m1x₁+a_m2x₂≤ b_m

x₁≥0 x₂ ≥0

c_j, b_i, a_ij –некотрые действительные числа

Из курса математики нам известно, что множество решений неравенства a₁₁x₁+a₁₂x₂≤ b₁

представляет собой одну из полуплоскостей вместе с прямой заданной уравнением a₁₁x₁+a₁₂x₂= b₁

Множество решений системы неравенств (2) представляют собой выпуклый многоугольник

Для уравнения прямой a_i1x₁+a_i2x₂≤ b_i упорядоченная пара чисел (a_i1, a_i2) ЗАДАЕТ КООРДИНАТЫ ВЕКТОРА НОРМАЛИ К ПРЯМОЙ

Определение:

Линии уравнения Z= с₁х₁+с₂х₂ называется множество точек координатной плоскости (х₁,х₂)координаты которой удовлетворяют неравенству с₁х₁+с₂х₂=к где к -константа

справедливы следующие утверждения

Теорема 1

Если задача линейного программирования (1) (2) имеет оптимальное решение, то целевая функция (1) достигает оптимального значения (максимума или минимума) в одной из вершин многоугольника, заданного системой неравенств (2)

Если целевая функция принимает оптимальное значение более чем в 1 вершине, то она достигает оптимума значения в любой точке прямой соединяющей эти вершины.

Теорема 2

Значение целевой функции (1) в точках линии уравнения увеличивается если линия уравнения перемещается параллельно начальному положению в направлении вектора нормали и уменьшается при перемещении в противоположном направлении.

Эти теоремы остаются справедливы для задач линейного программирования с любым конечным числом переменных.

 

Алгоритм графического метода решения ЗЛП

1 Построить многоугольник возможных (опорных) решений заданных системой ограничений (2)

2. Построить линию уравнения целевой функции (1) при к=0 (т.е. с₁х₁+с₂х₂=0)

3. найти вектор нормали

4. Передвигают прямую целевую функцию c₁x₂ + c₂x₂ = 0 в направлении вектора N до крайней точки многоугольника решений.

5. Вычисляют координаты точки и значение целевой функции в этой точке.

При этом могут возникать следующие ситуации:

1. Целевая функция принимает экстремальное (минимальное или максимальное) значение в единственной точке А.

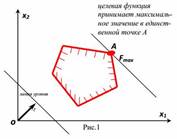
2. Целевая функция принимает экстремальное значение в любой точке отрезка АВ.

3. Целевая функция не ограничена сверху (при поиске на максимум) или снизу (на минимум)

4. Система ограничений задачи несовместна

 

Вопос № 9