Коефіцієнт кореляції Пірсона

Критерій незалежності х_і -квадрат Пірсона призначений для перевірки гіпотези про незалежність двох ознак, що задають рядки і стовпці таблиці спряженості. Статистика цього критерію

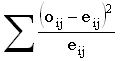
де сума береться по всіх клітках таблиці спряженості. Вона збігається зі статистикою критерію згоди х_і, специфіка складається лише в способі обчислення очікуваних зустрічальностей: e_ij=r_ic_j/N, де r_i – сума зустрічальностей у i-й рядку, c_j – сума зустрічальностей у j-м стовпці.

Критерій згоди хі-квадрат використовується для перевірки гіпотези про збіг емпіричного і теоретичного розподілів дискретних випадкових величин. Критерій ґрунтується на порівнянні спостережених і очікуваних (теоретичних) випадкових величин. Статистика критерію дорівнює сумі квадратів різниць між спостереженими й очікуваними зустрічальностями, ділених на очікувані випадкові

,

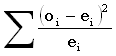де o_i – спостережена зустрічальність i-й градації,

e_i – її очікувана зустрічальність.

Зверніть увагу: значення статистики залежить від обсягу вибірки.

 

Розглянемо одну з основних задач математичної статистики - задачу про перевірку правдоподібності гіпотез. Перед дослідником завжди поставав питання: як установити, чи суперечать досвідчені дані гіпотезі про те, що СВ_Х розподілена за деяким законом. Для відповіді на це питання користаються так називаними критеріями згоди. Одним з таких критеріїв є критерій c ² - Пірсона. У чому його суть? Пірсон запропонував розрахувати теоретичні частоти реалізації СВ_Х, що підкоряється гіпотезі, що перевіряється, про закон розподілу, і порівняти їх з емпіричними за визначеним критерієм. Якщо критерій задовольняється, то гіпотеза про передбачуваний закон розподілу СВ_Х не відкидається, якщо критерій не задовольняється, те гіпотеза про передбачуваний закон розподілу СВ_Х відкидається і дослідник повинний висувати нову гіпотезу про закон розподілу СВ_Х (тобто переглянути свої погляди на природу досліджуваного явища).

Припустимо, що зроблено n незалежних досвідів, у кожнім з який СВ_Х прийняла визначене значення. Ці значення занесені в таблицю:

 

X	x1	x2	...	xk-1	xk
n	n1	n2	...	nk-1	nk
P*	p1*	p2*	...	pk-1*	pk*

 

Тут – частота події. Ми висуваємо гіпотезу Н₀, що складається в тім, що СВ_Х має розподіл

 

X	x1	x2	...	xk-1	xk
n	n1’	n2’	...	nk-1’	nk’
P*	p1*	p2*	...	pk-1*	pk*

 

 

Щоб перевірити правдоподібність цієї гіпотези, треба вибрати якусь міру розбіжності статистичного розподілу з гіпотетичним. Як міру розбіжності береться сума квадратів відхилення статистичних ймовірностей від гіпотетичних, узятих з деякими «вагами» с_j:

Коефіцієнти с_j уводяться тому, що відхилення, що відносяться до різних значень p_i, не можна вважати рівноправними: те саме по абсолютній величині відхилення може бути малозначним, якщо імовірність p_j велика, і дуже помітним, якщо вона мала.

Пірсон довів, що якщо прийняти , те при великому числі досвідів n закон розподілу величини R має дуже прості властивості: він практично не залежить від закону розподілу СВ_Х и мало залежить від числа досвідів n, а залежить тільки від числа значень випадкової величини (СВ_Х) k і при збільшенні n наближається до розподілу c ². При такому виборі коефіцієнтів c_j міра розбіжності R звичайно позначається c ² _набл:

чи з обліком того, що

,

одержимо

.

 

Величина R підкоряється розподілу c ² і залежить від параметра r, називаного "числом ступенів волі". При даному критерії число ступенів волі дорівнює числу значень СВ_Х k мінус число незалежних умов ("зв'язків"), накладених на частоти р^*.

Проста лінійна кореляція (Пірсона r). Кореляція Пірсона (далі називана просто кореляцією) припускає, що дві розглянуті перемінні обмірювані, принаймні, в інтервальній шкалі.

Вона визначає ступінь, з яким значення двох перемінних «пропорційні» один одному. Важливо, що значення коефіцієнта кореляції не залежить від масштабу виміру. Наприклад, кореляція між ростом і вагою буде однієї і тієї ж, незалежно від того, проводилися виміри в дюймах і чи фунтах у сантиметрах і кілограмах. Пропорційність означає просто лінійну залежність. Кореляція висока, якщо на графіку залежність "можна представити" прямою лінією (з позитивним чи негативним кутом нахилу).

 

 

Проведена пряма називається прямою регресії чи прямою, побудованою методом найменших квадратів. Останній термін зв'язаний з тим, що сума квадратів відстаней (обчислених по осі Y) від крапок, що спостерігаються, до прямої є мінімальної. Помітимо, що використання квадратів відстаней приводить до того, що оцінки параметрів прямої сильно реагують на викиди.

Як інтерпретувати значення кореляцій. Коефіцієнт кореляції Пірсона (r) являє собою міру лінійної залежності двох перемінних. Якщо звести його в квадрат, то отримане значення коефіцієнта детермінації r² представляє частку варіації, загальну для двох перемінних (іншими словами, "ступінь" чи залежності зв'язаності двох перемінних). Щоб оцінити залежність між перемінними, потрібно знати як «величину» кореляції, так і її значимість.

Коефіцієнт кореляції Пірсона за властивостями аналогічний коваріації, але завдяки нормуванню (у знаменнику – добуток стандартних відхилень обох величин) є безрозмірною величиною:

і набуває значень у інтервалі – 1≤ R_ху≤ 1.

 

Передумовами використання коефіцієнта кореляції Пірсона є:

1. Усі спостереження взаємно незалежні.

2. Спостереження мають нормальний закон розподілу.

На відміну від функціональної залежності, наприклад функції логарифму або синусу, коли кожному значенню однієї величини відповідає точно відоме значення другої, імовірнісний зв’язок характеризується тим, що кожному значенню однієї змінної відповідає множина значень другої змінної. Сила зв’язку характеризується також і абсолютною величиною коефіцієнта кореляції. Чим ближче до 1 або -1 значення кореляції, тим сильніший зв’язок. Якщо значення знаходиться ближче до 0, то це означає слабкий зв’язок.

Прикладом додатної кореляції є залежність між ростом людини та її вагою. Медики вважають, що коефіцієнт кореляції у цьому випадку дорівнює R=0,83. Слабка додатна кореляція R=0,12 спостерігається між властивістю людини до співчуття та реальною допомогою, яку вона реально надає.

Якщо коефіцієнт кореляції від’ємний, це означає наявність протилежного зв’язку: чим вище значення однієї змінної, тим нижче значення іншої. Тобто від’ємна кореляція означає те, що із збільшенням однієї величини друга має тенденцію до зменшення. Слабка від’ємна кореляція R=-0,13 спостерігається між агресивністю людини до своїх знайомих та допомогою, яку він їм надає. Чим більш агресивна людина, тим її допомога менша, але ця залежність не є сильною. Прикладом значної від’ємної кореляції R=-0,73 є залежність між нервовою збудженістю людини та її емоціональною рівновагою.

Якщо коефіцієнт кореляції близький до нуля, між величинами немає лінійного статистичного зв’язку, але не виключена наявність нелінійного зв’язку. Прикладом такого зв’язку є залежність зросту людини та його розумових здібностей.

Для словесного опису величини коефіцієнта кореляції використовуються такі градації.

Значення (по модулю)	Інтерпретація
До 0,2	Дуже слабка кореляція
До 0,5	Слабка кореляція
До 0,7	Середня кореляція
До 0,9	Висока кореляція
Понад 0,9	Дуже висока кореляція

 

Коефіцієнт кореляції є безрозмірною величиною, яка у даному вигляді характеризує ступінь залежності цих величин, котра виявляється в тім, що при зростанні однієї випадкової величини друга також виявляє тенденцію до зростання (чи убування). У першому випадку говорять, що випадкові величини пов'язані позитивною кореляцією, а в другому – кореляція негативна