«м≥ст
| ѕон€тт€ ковар≥ац≥њ ЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕ...... | |
| оеф≥ц≥Їнт корел€ц≥њ, його властивост≥ ЕЕЕЕЕЕЕЕ | |
| оеф≥ц≥Їнт корел€ц≥њ ѕ≥рсона ЕЕЕЕЕЕЕЕЕЕЕЕ. | |
| —писок використаноњ л≥тератури ЕЕЕЕЕЕЕЕЕЕ.. |
ѕон€тт€ ковар≥ац≥њ
ѕерев≥рка г≥потез про зв'€зки, €кщо мова йде про б≥льш н≥ж одн≥Їњ зм≥нноњ, припускаЇ одночасн≥ зм≥ни ≥ вим≥рюванн€ њх безв≥дносно до вказ≥вкам спр€мованост≥ вплив≥в (€ка з зм≥нних розгл€даЇтьс€ €к впливаЇ на ≥ншу). —татистичноњ м≥рою зв'€зку служить при цьому виб≥рковий коеф≥ц≥Їнт ковар≥ац≥њ Sxy. ¬≥н п≥драховуЇтьс€ €к середнЇ добутк≥в в≥дхилень кожноњ зм≥нноњ:
Sxy = 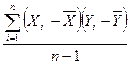
—аме ковар≥ац≥€ характеризуЇ зв'€зок двох зм≥нних ’ ≥ Y. овар≥ац≥€ даЇ к≥льк≥сну характеристику д≥аграми розс≥юванн€, на €к≥й зм≥нн≥ позначен≥ ос€ми, а окрем≥ спостереженн€, тобто отриман≥ емп≥ричн≥ дан≥, - точками в пр€мокутн≥й систем≥ координат. Ѕезл≥ч точок утворюЇ Ђхмаруї, за формою €кого суд€ть про зв'€зок зм≥нних ’ ≥ Y.
якщо зв'€зок позитивний, то б≥льш високим значенн€м одн≥Їњ зм≥нноњ (X) част≥ше в≥дпов≥дають ≥ б≥льш висок≥ значенн€ ≥ншоњ зм≥нноњ (Y).
овар≥ац≥€ даЇ к≥льк≥сну характеристику д≥аграми розс≥юванн€, на €к≥й зм≥нн≥ позначен≥ ос€ми, а окрем≥ спостереженн€, тобто отриман≥ емп≥ричн≥ дан≥, - точками в пр€мокутн≥й систем≥ координат. Ѕезл≥ч точок утворюЇ Ђхмаруї, за формою €кого суд€ть про зв'€зок зм≥нних ’ ≥ Y.
якщо зв'€зок позитивний, то б≥льш високим значенн€м одн≥Їњ зм≥нноњ (X) част≥ше в≥дпов≥дають ≥ б≥льш висок≥ значенн€ ≥ншоњ зм≥нноњ (Y). ÷ей випадок представлений на рис. 1. „им б≥льше за величиною коеф≥ц≥Їнт корел€ц≥њ, тим б≥льш вит€гнутим вигл€даЇ на д≥аграм≥ розс≥юванн€ це Ђхмаруї даних.
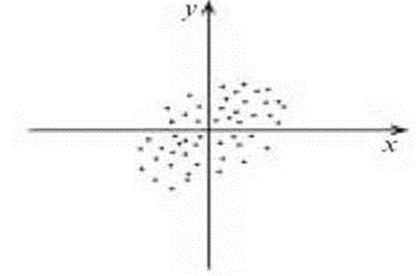
–ис. 1. ƒ≥аграма розс≥юванн€
«ауважимо, що ковар≥ац≥€ зм≥нноњ з самою собою - це дисперс≥€. ѕри обговоренн≥ трьох основних умов причинного виведенн€ стосовно до експериментальних даних йдетьс€ також про ковар≥ац≥ю незалежноњ ≥ залежноњ зм≥нних. ќднак тут маЇтьс€ на уваз≥ не випадков≥сть характеру зв'€зку м≥ж зм≥нами цих зм≥нних, а необх≥дн≥сть п≥драхунку коеф≥ц≥Їнту ковар≥ац≥њ. ƒл€ к≥льк≥сноњ оц≥нки експериментально отриманих ефект≥в зазвичай використовуютьс€ заходи в≥дм≥нностей, а не заходи зв'€зк≥в.
¬ластивост≥ ковар≥ац≥њ вивчаЇтьс€ у ковар≥ац≥йному анал≥з≥. овар≥ац≥йний анал≥з Ч це одночасний анал≥з сум квадрат≥в ≥ сум добутк≥в в≥дхилень двох або б≥льше зм≥нних в≥д њх середн≥х. ¬≥н використовуЇтьс€ при плануванн≥ ≥ статистичн≥й обробц≥ результат≥в досл≥д≥в €к спос≥б зменшенн€ помилки експерименту, €ка не п≥ддаЇтьс€ безпосередньому контролю (вим≥рюванню). овар≥ац≥йний анал≥з дозвол€Ї встановити сп≥вв≥дношенн€ м≥ж вар≥ац≥Їю залежноњ зм≥нноњ у ≥ вар≥ац≥Їю незалежноњ х.
оеф≥ц≥Їнт корел€ц≥њ, його властивост≥
¬ теор≥њ ймов≥рностей та математичн≥й статистиц≥, корел€ц≥€ Ї залежн≥стю двох випадкових величин. ѕри цьому, зм≥на одн≥Їњ або к≥лькох цих величин призводить до систематичноњ зм≥ни ≥ншоњ або ≥нших величин. ћатематичною м≥рою корел€ц≥њ двох випадкових величин слугуЇ коеф≥ц≥Їнт корел€ц≥њ.
|
|
|
орел€ц≥€ може бути позитивною та негативною (можлива також ситуац≥€ в≥дсутност≥ статистичного зв'€зку - наприклад, дл€ незалежних випадкових величин). Ќегативна корел€ц≥€ - корел€ц≥€, при €к≥й зб≥льшенн€ одн≥Їњ зм≥нноњ пов'€зане з≥ зменшенн€м ≥ншоњ, при цьому коеф≥ц≥Їнт корел€ц≥њ в≥д'Їмний. ƒодатна корел€ц≥€ - корел€ц≥€, при €к≥й зб≥льшенн€ одн≥Їњ зм≥нноњ пов'€зане з≥ зб≥льшенн€м ≥ншоњ, при цьому коеф≥ц≥Їнт корел€ц≥њ додатн≥й.
оеф≥ц≥Їнт корел€ц≥њ Ц показник, €кий використовують дл€ вим≥рюванн€ щ≥льност≥ зв'€зку м≥ж результативними ≥ факторними ознаками у корел€ц≥йно-регрес≥йн≥й модел≥ за л≥н≥йноњ залежност≥. «а абсолютною величиною коеф≥ц≥Їнту корел€ц≥њ коливаЇтьс€ в межах в≥д -1 до +1. „им ближчий цей показник до 0, тим менший зв'€зок, чим ближчий в≥н до ±1 Ц тим зв'€зок т≥сн≥ший. «нак Ђплюсї при коеф≥ц≥Їнт≥ корел€ц≥њ означаЇ пр€мий зв'€зок м≥ж ознаками х ≥ у, знак Ђм≥нусї Ц обернений.
”перше коеф≥ц≥Їнт корел€ц≥њ €к показник щ≥льност≥ зв'€зку використав . ѕ≥рсон. —початку досл≥джувалас€ пр€мол≥н≥йна залежн≥сть, пов'€зана ≥з законом нормального розпод≥лу (ј. Ѕраве, . ѕ≥рсон, ¬. Ўеппард та ≥н.), в≥дтак виникла потреба в досл≥дженн≥ й нел≥н≥йних залежностей. ƒл€ вим≥рюванн€ щ≥льност≥ зв'€зку нел≥н≥йних залежностей ѕ≥рсон запропонував корел€ц≥йне в≥дношенн€ ≥з розробкою метод≥в анал≥зу взаЇмозв'€зку двох зм≥нних було запропоновано теор≥ю часткових ≥ чистих коеф≥ц≥Їнт≥в корел€ц≥њ, а також теор≥ю множинноњ (багатофакторноњ) корел€ц≥њ.
оеф≥ц≥Їнт корел€ц≥њ м≥ж досл≥джуваними ознаками повинен мати високий р≥вень достов≥рност≥ (над≥йност≥). ƒл€ оц≥нки достов≥рност≥ коеф≥ц≥Їнту корел€ц≥њ обчислюють в≥дношенн€ коеф≥ц≥Їнта до його середньоњ помилки. якщо воно дор≥внюЇ або б≥льше 3, коеф≥ц≥Їнт корел€ц≥њ вважають достов≥рним, тобто зв'€зок м≥ж досл≥джуваними ознаками доведений. якщо в≥дношенн€ менше 3, то не можна зробити висновку про достов≥рн≥сть зв'€зку м≥ж досл≥джуваними ознаками. ƒл€ б≥льшоњ над≥йност≥ досл≥джень сп≥д брати величину в≥дношенн€ коеф≥ц≥Їнту корел€ц≥њ до його середньоњ помилки не 3, а 4. якщо в≥дношенн€ коеф≥ц≥Їнту корел€ц≥њ до його середньоњ помилки б≥льше 3, а число спостережень б≥льше 50, то вважають, що розрахований л≥н≥йний коеф≥ц≥Їнту корел€ц≥њ в≥дображаЇ ≥стотний т≥сний зв'€зок.
оеф≥ц≥Їнтом корел€ц≥њ ρху випадковоњ величини (х,у), називають в≥дношенн€
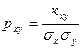
де σх, σу - середн≥ квадратичн≥ в≥дхиленн€ випадкових величин х та у.
оеф≥ц≥Їнт корел€ц≥њ незалежних випадкових величин дор≥внюЇ нулю. ¬ипадков≥ величини, дл€ €ких корел€ц≥йний момент (а значить ≥ коеф≥ц≥Їнт корел€ц≥њ) дор≥внюЇ нулю, називають некорельованими. ќчевидно, що дл€ некорельованост≥ випадкових величин достатньо, щоб њх сум≥сний розпод≥л був симетричний в≥дносно будь-€коњ пр€моњ, паралельноњ одн≥й з осей координат.
«ауважимо, що р≥вн≥сть нулю коеф≥ц≥Їнта корел€ц≥њ Ц необх≥дна, але не достатн€ умова незалежност≥ випадкових величин.
ќтже, з некорельованост≥ випадкових величин не завжди випливаЇ њх незалежн≥сть. оеф≥ц≥Їнт корел€ц≥њ характеризуЇ не будь-€ку залежн≥сть, а т≥льки так звану л≥н≥йну, €ка пол€гаЇ в тому, що при зростанн≥ одн≥Їњ з випадкових величин ≥нша зростаЇ (або спадаЇ) за л≥н≥йним законом. якщо випадков≥ величини х та у мають точно л≥н≥йну функц≥ональну залежн≥сть х=aу+b, то ρху=±1 причому, €кщо a>0 ρху=1, а €кщо a<0 ρху=-1. ¬ загальному значенн€ коеф≥ц≥Їнта корел€ц≥њ ρху задовольн€ють нер≥вн≥сть: -1 ≤ ρху ≤ 1.
|
|
|
¬ластивост≥ коеф≥ц≥Їнта корел€ц≥њ пол€гають в наступному:
1. оеф≥ц≥Їнт корел€ц≥њ Ї в межах в≥д -1 до +1.
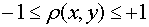
якщо 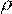 (x, y) > 0, то корел€ц≥€ пр€ма, а €кщо
(x, y) > 0, то корел€ц≥€ пр€ма, а €кщо 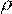 (x, y) < 0 Ц зворотна. ѕр€ма корел€ц≥€: б≥льшим значенн€м випадковоњ зм≥нноњ x в≥дпов≥дають б≥льш≥ значенн€ y; зворотна корел€ц≥€: б≥льшим значенн€м x в≥дпов≥дають менш≥ y ≥ навпаки, б≥льшим y Ц менш≥ x.
(x, y) < 0 Ц зворотна. ѕр€ма корел€ц≥€: б≥льшим значенн€м випадковоњ зм≥нноњ x в≥дпов≥дають б≥льш≥ значенн€ y; зворотна корел€ц≥€: б≥льшим значенн€м x в≥дпов≥дають менш≥ y ≥ навпаки, б≥льшим y Ц менш≥ x.
2. —иметр≥€
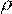 (x, y) =
(x, y) = 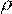 (y, x)
(y, x)
3. якщо x та y повТ€зан≥ л≥н≥йним функц≥ональним звТ€зком y (x) = a + bx, a ≥ b Ц стал≥, то 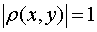 , ≥ навпаки.
, ≥ навпаки.
4. якщо випадков≥ зм≥нн≥ л≥н≥йно незалежн≥, то 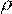 (x, y) = 0, ≥ навпаки.
(x, y) = 0, ≥ навпаки.
ќстанн≥ дв≥ властивост≥ можна сформулювати €к необх≥дну й достатню умови, причому критер≥Їм залежност≥ випадкових величин x ≥ y Ї в≥дм≥нн≥сть коеф≥ц≥Їнта корел€ц≥њ в≥д нул€: 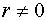 .
.






