¬раховуючи, що з великоњ к≥лькост≥ можливих вар≥ант≥в зТЇднанн€ –¬ м≥ж собою переважна частина не задовольн€Ї умовам зниженн€ витрат на перевезенн€ ≥ обробленн€ пошти та не забезпечуЇ можливост≥ виконанн€ нормативних строк≥в пересиланн€ пошт≥вок, доц≥льно розгл€нути ≥ пор≥вн€ти лише принципово р≥зн≥ структури маг≥стральних мереж поштового звТ€зку.
ласиф≥кац≥ю структур маг≥стральних мереж поштового звТ€зку наведено на рис. 3.7.

–исунок 3.7. ласиф≥кац≥€ структур маг≥стральних мереж поштового звТ€зку
—труктури маг≥стральних мереж ћѕ«-1, ћѕ«-2,..., ћѕ«-6 наведено на рис. 3.8 (жирними л≥н≥€ми позначен≥ маг≥стральн≥ звТ€зки).

–исунок 3.8. —труктури маг≥стральних мереж поштового звТ€зку
—труктури ћѕ«-1, ћѕ«-2 Ц без транзитного обробленн€ пошти; структури ћѕ«-3, ћѕ«-4 Ц з одним транзитним обробленн€м пошти; структура ћѕ«-5 Ц з двома транзитними обробленн€ми пошти; структура ћѕ«-6 Ц з трьома транзитними обробленн€ми пошти.
¬ структур≥ ћѕ«-1 ќ¬ зТЇднан≥ за принципом Д ожний з кожнимФ.
ќск≥льки в ћѕ«-1 кожний поштовий маршрут зТЇднуЇ лише два ќ¬, к≥льк≥сть поштових маршрут≥в в пр€мому ≥ зворотному напр€мах визначаЇтьс€ тим, що кожний з n ќ¬ мереж≥ зТЇднаний поштовими маршрутами з рештою n - 1 ќ¬ ≥ складаЇ N ћѕ«-1 = n (n Ц 1).
«агальна к≥льк≥сть поштових маршрут≥в в ћѕ«-2 залежить в≥д к≥лькост≥ ќ¬, що зТЇднуютьс€ поштовими маршрутами.
ƒл€ розрахунку зазначеноњ к≥лькост≥ роз≥бТЇмо n ќ¬ ћѕ«-2 на k груп, кожна з €ких включаЇ n 1, n 2,..., nk ќ¬, що розташован≥ на м≥н≥мальних в≥дстан€х один в≥д одного.
ожну з одержаних груп ќ¬ зТЇднаЇмо поштовим маршрутом з кожною з решти груп, внасл≥док чого загальна к≥льк≥сть таких поштових маршрут≥в складе N ћѕ«-2 = k (k Ц 1), причому кожний з маршрут≥в, що зТЇднуЇ будь-€к≥ дв≥ групи ќ¬, одночасно зТЇднуЇ також ус≥ ќ¬, включен≥ до кожноњ з зазначених груп.
«окрема, €кщо n 1 = n 2 =... = nk = n / k, к≥льк≥сть ќ¬, €ку зТЇднаЇ кожний поштовий маршрут ћѕ«-2, складе 2 n / k.
Ќа рис. 3.8 ћѕ«-2 м≥стить n = 6 ќ¬, розбитих на k = 3 групи по n / k = 6/3 = 2 ќ¬ в кожн≥й, внасл≥док чого загальна к≥льк≥сть поштових маршрут≥в складаЇ k (k Ц 1) = 3×2 = 6, а к≥льк≥сть ќ¬, зТЇднаних одним поштовим маршрутом, складаЇ 2 n / k = 12 / 3 = 4.
√рупуванн€ ќ¬ дозвол€Ї суттЇво скоротити €к к≥льк≥сть поштових маршрут≥в, що використовуютьс€ дл€ зТЇднанн€ зазначених ќ¬ м≥ж собою, так ≥ њх загальну прот€жн≥сть.
“ак, €кщо вважати, що ќ¬ ћѕ«-1 ≥ ћѕ«-2 на рис. 3.8 розташован≥ у вершинах правильних шестикутник≥в, сторони €ких дор≥внюють одиниц≥, то в ћѕ«-1, де кожний поштовий маршрут зТЇднуЇ лише 2 ќ¬, використовуЇтьс€ 30 поштових маршрут≥в загальною прот€жн≥стю L ћѕ«-1 = 44,78, а в ћѕ«-2, де кожний поштовий маршрут зТЇднуЇ 4 ќ¬, 2 з €ких розташован≥ в одн≥й груп≥, а 2 Ц в ≥нш≥й, використовуЇтьс€ т≥льки 6 поштових маршрут≥в загальною прот€жн≥стю L ћѕ«-2 = 18.
” мережах з транзитним обробленн€м пошти ћѕ«-3, ћѕ«-4, ћѕ«-5, ћѕ«-6 на рис. 3.8 застосовано нумерац≥ю вузл≥в, зручну дл€ розрахунк≥в загальноњ прот€жност≥ поштових марщрут≥в, що в них використовуютьс€.
|
|
|
ѕри цьому прийн€т≥ наступн≥ позначенн€:
n Ц загальна к≥льк≥сть ќ¬, нумерац≥€ вузл≥в 0, 1,..., n - 1;
m Ц загальна к≥льк≥сть –¬, нумерац≥€ вузл≥в 0, 1,..., m - 1;
0 Ц позначенн€ номера √¬;
1, 2,..., m Ц 1 Ц позначенн€ номер≥в –¬;
n 0 Ц позначенн€ к≥лькост≥ ќ¬, п≥дпор€дкованих √¬;
n 1,..., nm -1 Ц позначенн€ к≥лькост≥ ќ¬, п≥дпор€дкованих –¬ 1, 2,..., m - 1;
m, m + 1,..., m + n 0 Ц 1 Ц позначенн€ номер≥в ќ¬, п≥дпор€дкованих √¬;
m + n 0 , m + n 0 + 1,..., m + n 0 + n 1 - 1;...; m + n 0 + n 1 +... + nm -2 , m + n 0 + n 1 +... + nm -2 + 1,..., m + n 0 + n 1 +... + nm -1 - 1 Ц позначенн€ номер≥в ќ¬, п≥дпор€дкованих –¬ 1, 2,..., m - 1.
јнал≥з структур мереж ћѕ«-3, ћѕ«-4, ћѕ«-5, ћѕ«-6, наведених на рис. 3.8, св≥дчить, що сумарна прот€жн≥сть поштових маршрут≥в будь-€коњ з них визначаЇтьс€ комб≥нац≥Їю прот€жностей пТ€ти складових зазначених маршрут≥в:
- сумарноњ прот€жност≥ поштових маршрут≥в, що зТЇднують √¬ з –¬
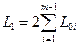 ;
;
- сумарноњ прот€жност≥ поштових маршрут≥в, що зТЇднують √¬ з п≥дпор€дкованими йому ќ¬
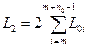 ;
;
- сумарноњ прот€жност≥ поштових маршрут≥в, що зТЇднують √¬ з ќ¬, п≥дпор€дкованими в≥дпов≥дним –¬
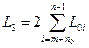 ;
;
- сумарноњ прот€жност≥ поштових маршрут≥в, що зТЇднують –¬ з п≥дпор€дкованими њм ќ¬
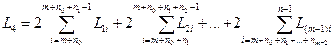 ;
;
- сумарноњ прот€жност≥ поштових маршрут≥в, що зТЇднують –¬ м≥ж собою
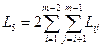 .
.
¬иход€чи з наведених значень L 1, L 2, L 3, L 4, L 5, сумарн≥ прот€жност≥ поштових маршрут≥в ћѕ«-3, ћѕ«-4, ћѕ«-5, ћѕ«-6 складають:
L ћѕ«-3 = L 1 + L 2 + L 3;
L ћѕ«-4 = L 1 + L 2 + L 3 + L 4;
L ћѕ«-5 = L 1 + L 2 + L 4 + L 5;
L ћѕ«-6 = L 1 + L 2 + L 4 .
« анал≥зу отриманих вираз≥в випливаЇ:
- прот€жност≥ поштових маршрут≥в ус≥х мереж м≥ст€ть складов≥ L 1 + L 2;
- враховуючи, що L 4 < L 3, прот€жн≥сть L ћѕ«-6 = min;
- приймаючи, €к це маЇ м≥сце на практиц≥, L 3 ≈ L 4 + L 5, прот€жност≥ L ћѕ«-3 ≈ L ћѕ«-5;
- прот€жн≥сть L ћѕ«-4 = max.
«в≥дси випливаЇ
min= L ћѕ«-6 < L ћѕ«-3 ≈ L ћѕ«-5 < L ћѕ«-4 = max.
Ќа рис. 3.9 наведено граф взаЇмозвТ€зк≥в сумарних прот€жностей поштових маршрут≥в ћѕ«-3, ћѕ«-4, ћѕ«-5, ћѕ«-6.

–исунок 3.9. √раф взаЇмозвТ€зк≥в сумарних прот€жностей поштових маршрут≥в ћѕ«-3, ћѕ«-4, ћѕ«-5, ћѕ«-6
«агальна к≥льк≥сть поштових маршрут≥в в ћѕ«-3 ≥ ћѕ«-6 м≥н≥мальна ≥ складаЇ N ћѕ«-3 = N ћѕ«-6 = n - 1, оск≥льки структури цих мереж Ї графами-деревами.
«агальна к≥льк≥сть поштових маршрут≥в в ћѕ«-5 у пор≥вн€нн≥ з ћѕ«-6 зростаЇ за рахунок упровадженн€ маршрут≥в, що зТЇднують –¬ м≥ж собою, а в ћѕ«-4 Ц за рахунок упровадженн€ маршрут≥в, що зТЇднують ќ¬, п≥дпор€дкован≥ –¬, з √¬.
” табл. 3.4 наведено узагальнен≥ показники мереж поштового звТ€зку з транзитним обробленн€м пошти.
“аблиц€ 3.4. ”загальнен≥ показники мереж поштового звТ€зку з транзитним обробленн€м пошти
| ѕоказники | ћѕ«-3 | ћѕ«-4 | ћѕ«-5 | ћѕ«-6 |
| «агальна к≥льк≥сть поштових маршрут≥в | м≥н≥мальна | максимальна | середн€ | м≥н≥мальна |
| —умарна прот€жн≥сть поштових маршрут≥в | середн€ | максимальна | середн€ | м≥н≥мальна |
| ≥льк≥сть транзитних вузл≥в, зад≥€них у пересиланн≥ пошти м≥ж ќ¬ | ||||
| ≥льк≥сть поштових маршрут≥в, зад≥€них у пересиланн≥ пошти м≥ж ќ¬ | ||||
| —умарна к≥льк≥сть транзитних вузл≥в ≥ поштових маршрут≥в, зад≥€них у пересиланн≥ пошти м≥ж ќ¬ | ||||
| «атримка часу пересиланн€ пошти м≥ж ќ¬ | м≥н≥мальна | м≥н≥мальна | середн€ | максимальна |
|
|
|
ћ≥н≥мальною структурою мереж≥ поштового звТ€зку Ї структура ћѕ«-3 з √¬ у иЇв≥, €ка передбачаЇ зТЇднанн€ ус≥х ќ¬ м≥ж собою через зазначений √¬.
як доведено нижче, при створенн≥ в ”крањн≥ одного √¬ у иЇв≥, в≥н здатний забезпечити автоматизоване сортуванн€ ус≥Їњ письмовоњ кореспонденц≥њ ”крањни €к за умов ≥снуючих обс€г≥в письмовоњ кореспонденц≥њ, так ≥ за умов њх суттЇвого зростанн€ у майбутньому.
¬иход€чи з цього, вир≥шальним чинником створенн€ ≥нших поштових рег≥он≥в Ї м≥н≥м≥зац≥€ витрат на перевезенн€ ≥ обробленн€ посилочноњ пошти, а також скороченн€ нормативних строк≥в пересиланн€ пошт≥вок в рег≥онах.
¬раховуючи, що створенн€ нових поштових рег≥он≥в призводить, з одного боку, до скороченн€ витрат на перевезенн€ ≥ обробленн€ посилочноњ пошти за рахунок зам≥ни перевезенн€ посилочноњ пошти б≥льш прот€жними маршрутами через √¬ у иЇв≥ менш прот€жними маршрутами через –¬ в≥дпов≥дних рег≥он≥в, а, з ≥ншого, Ц до њх зростанн€ внасл≥док упровадженн€ нових рег≥ональних маршрут≥в, створенн€ нових рег≥он≥в доц≥льне, €кщо зазначене скороченн€ витрат на перевезенн€ посилочноњ пошти перевищуЇ њх зростанн€, ≥ недоц≥льне у протилежному випадку.
ќск≥льки тепер≥шнього часу згадане сп≥вв≥дношенн€ виконуЇтьс€ лише у п≥вденно-сх≥дному (–¬ у ƒн≥пропетровську) ≥ зах≥дному (–¬ у Ћьвов≥) рег≥онах, в структур≥ ћѕ«-4 передбачено створенн€ зазначених поштових рег≥он≥в.
«а умов виконанн€ згаданих сп≥вв≥дношень в ≥нших рег≥онах ”крањни, к≥льк≥сть створюЇмих поштових рег≥он≥в буде в≥дпов≥дно зростати.






