Тема 9. Изучение взаимосвязей

Задание 1.

Таблица 9.1

№ пред-приятия	Объем реализованной продукции xi, млн. руб.	Прибыль yi, мнл. руб.	xi-xср	(xi-xср)2	yi-yср	(yi-yср)2	(xi-xср) (yi-yср)
		21,4	14,25	203,06	5,50	30,25	78,375
		20,2	5,25	27,56	4,30	18,49	22,575
		14,2	4,25	18,06	-1,70	2,89	-7,225
		14,3	1,25	1,56	-1,60	2,56	-2
			-0,75	0,56	-2,90	8,41	2,175
			-2,75	7,56	-0,90	0,81	2,475
		17,1	-3,75	14,06	1,20	1,44	-4,5
			-17,75	315,06	-3,90	15,21	69,225
Сумма		127,2		587,50		80,06	161,1

x_ср=77,75 млн. руб.; y_i=15,9 млн. руб.

В случае линейной зависимости уравнение регрессии является уравнением прямой линии. Таких уравнений два:

Y = a₁ + b_y/xX — прямое
и X = a₂ + b_x/yY — обратное,

где: a и b – коэффициенты, или параметры, которые надлежит определить. Значение коэффициентов регрессии вычисляется по формуле:

.

Коэффициенты регрессии b имеют размерность, равную отношению размерностей изучаемых показателей X и Y, и тот же знак, что и коэффициент корреляции.

Коэффициенты а определяются по формуле:

.

Чтобы вычислить этот коэффициенты, надо просто в уравнения регрессии подставить средние значения коррелируемых переменных.

;

;

;

.

Уравнение прямой парной линейной регрессии: Y=-5,09+0,27X;

Уравнение обратной парной линейной регрессии: X=45,79+2,01Y.

Определим уравнение обратной линейной зависимости (гиперболы).

Подставив в данную систему, например, первые значения x и y из таблицы 9.1, определим значения коэффициентов a и b. Они равны a= -0,058, b=1224.

Уравнение обратной линейной зависимости имеет вид: .

 

Рис. 9.1. Уравнения парной линейной регрессии и обратной линейной зависимости (гиперболы)

 

Определим коэффициент корреляции по формуле:

.

Для уравнения парной линейной регрессии: .

Для уравнения обратной линейной зависимости составим расчетную таблицу 9.2.

Таблица 9.2

Расчет параметров уравнения гиперболы

№ пред-приятия	Объем реализованной продукции xi, млн. руб.	Прибыль yi, мнл. руб.	xi-xср	(xi-xср)2	yi-yср	(yi-yср)2	(xi-xср) (yi-yср)
	92,00	13,25	14,25	203,06	-2,65	7,02	-37,75
	83,00	14,69	5,25	27,56	-1,21	1,46	-6,33
	82,00	14,87	4,25	18,06	-1,03	1,05	-4,36
	79,00	15,44	1,25	1,56	-0,46	0,21	-0,57
	77,00	15,84	-0,75	0,56	-0,06	0,00	0,04
	75,00	16,26	-2,75	7,56	0,37	0,13	-1,01
	74,00	16,48	-3,75	14,06	0,59	0,34	-2,20
	60,00	20,34	-17,75	315,06	4,45	19,77	-78,92
Сумма		127,16	-	587,50	-	29,99	-131,11

Коэффициент корреляции для уравнения гиперболы:

.

Возможные значения степени тесноты корреляционной свя­зи, измеряемой данными коэффициентами корреляции, лежат в пределах от —1 до +1. Коэффициенту, равному — 1, соответствует полная обратная связь, 0 — отсутствие всякой связи, +1 — пол­ная прямая связь, а дробным значениям — определенная сте­пень прямой или обратной связи.

Для уравнения парной линейной регрессии соответствует полная прямая связь, в то время как для уравнения обратной линейной зависимости – полная обратная связь.

Элементарной характеристикой тесноты связи между двумя признаками х и у является коэффициент Фехнера. В основе его расчета лежит принцип сопоставления не абсолютных значений признаков х и у, а их отклонений от среднего уровня. Коэффициент Фехнера определяется по следующей формуле: ,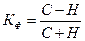

где С - число совпадений знаков отклонений (например, “плюс” и

“плюс”, “минус” и “минус”, “отсутствие отклонения” и “отсутствие

отклонения”);

Н - число несовпадений знаков отклонений.

Коэффициент Фехнера может принимать значения в пределах от -1 до 1. При +1 име­ется полная прямая согласованность, при 0 — изменчивость ни­как не согласуется, при — 1 - полная обратная несогласован­ность.

В уравнении парной линейной регрессии все отклонения по знакам совпали (см. таблицу 9.2), поэтому . А в уравнении обратной зависимости . В первом случае , что свидетельствует о существенной прямой со­гласованности. Во втором случае при 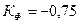- полная обратная несогласованность.

Таблица 9.3

Определение коэффициента Фехнера

Прямое уравнение Y=-5,09+0,27X	Уравнение обратной зависимости Y=-0,058+1224/X
x	y	xi-xср	yi-yср	x	y	xi-xср	yi-yср
92,00	19,75	14,25	3,85	92,00	13,25	14,25	-2,65
83,00	17,32	5,25	1,42	83,00	14,69	5,25	-1,21
82,00	17,05	4,25	1,15	82,00	14,87	4,25	-1,03
79,00	16,24	1,25	0,34	79,00	15,44	1,25	-0,46
77,00	15,70	-0,75	-0,20	77,00	15,84	-0,75	-0,06
75,00	15,16	-2,75	-0,74	75,00	16,26	-2,75	0,36
74,00	14,89	-3,75	-1,01	74,00	16,48	-3,75	0,58
60,00	11,11	-17,75	-4,79	60,00	20,34	-17,75	4,44

При оценке тесноты связи между количественными признаками используется коэффициент корреляции рангов (коэффициент Спирмена):

,

где di - квадраты разности рангов;

n – число наблюдений (число пар рангов).

Коэффициент Спирмена может принимать значения в пределах от -1 до 1.

Коэффициент Спирмена рассчитывается следующим образом (таблица

9.3):

1) ранжируем значения признака x по возрастанию (графа 4), каждому значению признака x присваиваем порядковый номер – ранг (графа 5).

2) ранжируем значения признака у по возрастанию (графа 6), каждому значению признака у присваиваем ранг (графа 7).

3) возвращаемся к исходному ряду значений признака x (графа 2) и в графе 8 ставим его порядковый номер, аналогичную процедуру проводим для признака у.

4) находим разность рангов di = Rx − Ry.

5) определяем величину d_i²и находим коэффициент Спирмена.

 

Таблица 9.4

Расчет коэффициента Спирмена для уравнения парной линейной регрессии

№	Цена спроса x	Цена предложения y	Ранжирование	Сравнение рангов	Разность рангов di=Rx-Ry	di2
x	Rx	y	Ry	Rx	Ry
		21,4
		20,2
		14,2			14,2
		14,3			14,3
					17,1
		17,1			20,2
					21,4
Итого

 

 

Таблица 9.5

Расчет коэффициента Спирмена для уравнения обратной линейной зависимости (гиперболы)

№	Цена спроса x	Цена предложения y	Ранжирование	Сравнение рангов	Разность рангов di=Rx-Ry	di2
x	Rx	y	Ry	Rx	Ry
	92,00	13,25			13,25
	83,00	14,69			14,69
	82,00	14,87			14,87
	79,00	15,44			15,44
	77,00	15,84			15,84				-3
	75,00	16,26			16,26				-2
	74,00	16,48			16,48				-4
	60,00	20,34			20,34				-7
Итого

.

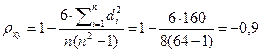Таблица 9.6

Значения коэффициентов для двух моделей

Коэффициенты	Уравнение парной линейной регрессии Y=-5,09+0,27X	Уравнение обратной линейной зависимости (гипербола)
Корреляции	0,74	-0,99
Фехнера		-0,75
Спирмена		-0,9

На основании таблицы 9.6 можно сделать вывод о том, что наилучшей моделью является уравнение парной линейной регрессии, поскольку при сравнении трех различных коэффициентов (корреляции, Фехнера и Спирмена) в этом модели наблюдается полная прямая связь между объемом реализованной продукции и прибылью, а в модели обратной линейной зависимости – полная обратная связь.

Задание 2.

При оценке тесноты связи между количественными признаками используется коэффициент корреляции рангов (коэффициент Спирмена):

,

где di - квадраты разности рангов;

n – число наблюдений (число пар рангов).

Коэффициент Спирмена может принимать значения в пределах от -1 до 1.

Коэффициент Спирмена рассчитывается следующим образом (таблица

9.3):

1) ранжируем значения признака x по возрастанию (графа 4), каждому значению признака x присваиваем порядковый номер – ранг (графа 5).

2) ранжируем значения признака у по возрастанию (графа 6), каждому значению признака у присваиваем ранг (графа 7).

3) возвращаемся к исходному ряду значений признака x (графа 2) и в графе 8 ставим его порядковый номер, аналогичную процедуру проводим для признака у.

4) находим разность рангов di = Rx − Ry.

5) определяем величину d_i²и находим коэффициент Спирмена.

 

Таблица 9.4

Расчет коэффициента Спирмена

№	Цена спроса x	Цена предложения y	Ранжирование	Сравнение рангов	Разность рангов di=Rx-Ry	di2
x	Rx	y	Ry	Rx	Ry
									-1
									-2
Итого	-	-	-	-	-	-	-	-	-

.

Следовательно, связь между ценой спроса и ценой предложения прямая и умеренная.

Тема 10. Индексы

Индекс – это показатель сравнения двух состояний одного и того же явления (простого или сложного, состоящего из соизмеримых или несоизмеримых элементов). Индекс, который строится как сравнение обобщенных величин, называется сводным или общим, и обозначается I. Если же сравниваются необобщенные величины, то индекс называется индивидуальным и обозначается i.

Задание 1.

Таблица 10.1

Культура	Посевная площадь, тыс. га	Урожайность, ц/га	Сбор урожая, тыс. ц
1998 q0	2000 q1	1998 p0	2000 p1	1998 q0p0	2000 q1p1	q0p1	q1p0
Пшеница	16,5	9,7	24,3	30,1	400,95	291,97	731,43	235,71
Ячмень	3,4	6,6	20,1	16,8	68,34	110,88	337,68	132,66
Кукуруза	0,53	1,28	37,3	36,2	19,77	46,34	1350,26	47,74
Итого	20,43	17,58	81,70	83,10	489,06	449,19	2419,37	416,11

 

Таблица 10.2

Изменение сбора зерновых культур тысяча центнерах по сравнению 2000 года с 1998

Культура	Общее	Размера посевных площадей	Урожайности	Структуры
Пшеница	-108,98	-165,24	56,26	-204,68
Ячмень	42,54	64,32	-21,78	53,76
Кукуруза	26,567	27,975	-1,408	27,15
Итого	-39,873	-72,945	33,072	-123,77
Агрегатный индекс	0,92	0,85	1,08	0,19

 

Для расчета изменений сбора зерновых культур использовались следующие формулы:

1. Для общего изменения: .

2. Для изменения размера посевных площадей: .

3. Для изменения урожайности: .

4. Для изменения структуры посевных площадей: .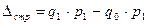

Для расчета агрегатных индексов использовались следующие формулы:

1. Для общего индекса: .

2. Для индекса с учетом изменения размера посевных площадей: .

3. Для индекса с учетом изменения урожайности: .

4. Для индекса с учетом изменения структуры посевных площадей: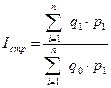

 

Рис. 10.1. Величина посевных площадей по зерновым культурам за 1998, 2000 год

 

 

Рис. 10.2. Урожайность по зерновым культурам за 1998, 2000 год

 

 

Рис. 10.3. Изменений сбора зерновых культур за 1998, 2000 год

 

Задание 2.

Задание 3.

Таблица 10.3

Продукт	Город А	Город Б	Выручка, руб.	Индексы цен города А по отношению к городу Б
Объем реализации, т	Цена за 1 кг, руб	Объем реализации, т	Цена за 1 кг, руб	Город А	Город Б
Молоко							0,78
Мясо							1,40
Хлеб							7,17
Итого	-	-	-	-			2,35

 

Для расчета индексов использовались следующие формулы:

1. Для индивидуальных индексов: .

2. Для сводного индекса: .