Задание 1.
Таблица 5.1
| Месяц | Объем продаж, тыс руб | Относительные показатели динамики по отношению к январю, % | Цепные показатели динамики | |
| Абсолютные, тыс. руб. | Относительные, % | |||
| январь | - | - | - | |
| февраль | -4 | |||
| март | ||||
| апрель | -5 | |||
| май | ||||
| июнь | -6 |
Таблица 5.2
| Среднемесячный объем продаж, тыс. руб. | Средний цепной показатель динамики | Медиана | |
| Абсолютные, тыс. руб. | Относительные, % | ||
| 103,5 | 0,8 |
Задание 2.
Таблица 5.3
| Предприятие | Месячный фонд заработной платы, тыс. руб. | Средняя заработная плата, руб. | ОПС для месячного фонда з\п, % | ОПС для средней з\п, % |
| Цементный завод | 39,54 | 39,36 | ||
| Молокозавод | 25,30 | 24,70 | ||
| Мебельный комбинат | 35,16 | 35,94 | ||
| Сумма | 100,00 | 100,00 |
Относительный показатель структуры (ОПС) определяется по формуле:
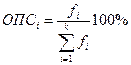
Относительные показатели координации (ОПК) характеризуют соотношение отдельных частей целого между собой при этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес. В результате получают сколько единиц каждой структурной части приходится на одну единицу (сто, тысячу и т.д.) базисной структурной части. За базу примем месячный фонд оплаты труда цементного завода (586 тыс. руб.). Получаем: ОПК молокозавода составляет 375/586*100%=64% и ОПК мебельного комбината 521/586*100%=89% относительно цементного завода. Аналогично ОПК рассчитываем и для средней заработной платы: ОПК молокозавода - 63%, ОПК мебельного комбината – 91,3% относительно цементного завода.
Средняя заработная плата: 
руб.
Значение моды для заработной платы равно 1195 руб.
Рис. 5.1. Диаграмма месячного фонда заработной платы
Рис. 5.2. Диаграмма средней заработной платы
Задание 3.
Таблица 5.4
| Цена 1м2 (в $) | Общая площадь (в тыс. м2), f | Середина интервала, х | f*x | Накопленная частота, f1 | Относительные показатели структуры, % |
| 100-200 | 38.1 | 38.1 | 36.63 | ||
| 200-300 | 28.5 | 66.6 | 27.40 | ||
| 300-400 | 15.4 | 14.81 | |||
| 400-500 | 14.42 | ||||
| 500-600 | 6.73 | ||||
| Сумма |
Относительный показатель структуры определяется по формуле:
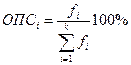
Модой (обозначим Мо) называется варианта, наиболее часто встречающаяся в данном вариационном ряду. Для дискретного ряда мода равна варианте с наибольшей частотой или частостью. В нашем случае наибольшая площадь 38,1 тыс. м2, это и будет модой.
Медианой (обозначим Mе) называется такое значение варьирующего признака, которое приходится на середину вариационного ряда.
При нахождении медианы дискретного вариационного ряда могут возникнуть два случая: 1) число вариант нечетно (k=2m+1), 2) число вариант четно (k=2m). В первом случае Me=xm+1, т. е. медиана равна центральной (срединной) варианте ряда, во втором случае Me=(xm+xm+1)/2, т.е. медиана принимается равной полу сумме находящихся в середине ряда вариант.
В нашем случае число вариант – 5, медиана равна центральной (срединной) варианте ряда, т.е. Mе=15,4 тыс. м2.
Гистограмма распределения применяется для изображения интервального ряда. Для построения гистограммы на горизонтальной оси откладывают последовательно отрезки, равные интервалам признака, и на этих отрезках, как на основаниях, строят прямоугольники, высоты которых равны частотам.
Кумулята есть графическое изображение вариационного ряда, когда на вертикальной оси откладываются накопленные частоты или частности, а на горизонтальной - значения признака. Кумулята служит для графического представления как дискретных, так и интервальных вариационных рядов.
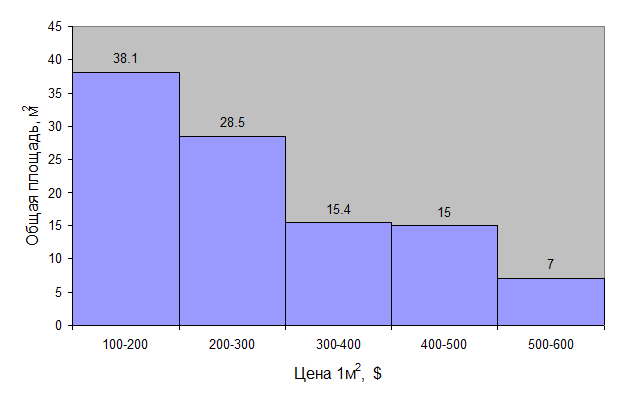
Рис.5.3. Гистограмма данных стоимости жилья
Средняя цена 1 тыс. м2 жилья: 
$
Средняя цена 1 м2 жилья: 
$
Рис.5.4. Кумулята данных стоимости жилья
Когда значение находится в зоне, где расположено менее 25% наблюдаемых значений переменной, то говорят, что оно расположено в нижнем квартиле (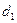
). При помощи программы Microsoft Office Excel и встроенного в него пакета анализа определяем значение первой квартили для: 1) общей площади: 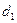= 15 (тыс. м2); 2) цены за 1 м2: 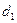= 250 $.
