Задание 1.
N=625
Xср=1204 руб.
СКО=104 руб.
F(t)=0,95; t=1,96.
Найти 95% доверительный интервал для значений средней заработной платы рабочих в промышленности.
Определим скорректированную дисперсию: 
; 
.
Средняя ошибка выборки: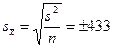 
руб.
Отклонение выборочной средней от генеральной с вероятностью 95% составит:
руб.
Определим доверительный интервал:
;
.
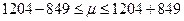Задание 2.
Таблица 7.1
| Возраст xi | Число студентов fi | xi * fi | (xi -xср)2* fi |
| 146,21 | |||
| 68,45 | |||
| 7,23 | |||
| 0,29 | |||
| 10,58 | |||
| 83,20 | |||
| 69,46 | |||
| 103,34 | |||
| сумма | 488,75 |
Средний возраст студентов выборки: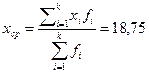 
;
Среднеквадратическое отклонение возраста по выборке:
.
F(t)=0,99; t=2,62.
Определим скорректированную дисперсию: ;
Средняя ошибка выборки: 
Отклонение выборочной средней от генеральной с вероятностью 99% составит:
Определим доверительный интервал:
;
.
Доля 20-летних студентов в выборке составляет 13%, значит p=0,87;
.
Пределы для доли 20-летних студентов для доверительной вероятности составляют: 
или 
Задание 3.
F(t)=0,99; t=2,5758;
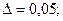
Определить сколько нужно обследовать семей, чтобы с вероятностью 0,99 и точностью не менее 0,5% определить эту долю.
.
Задание 4.
F(t)=0,99; t=2,58.
Определяем доверительный интервал для мужчин.
n=108; 
=20 мин; xср=150 мин.
Определим скорректированную дисперсию: ;
Средняя ошибка выборки: 
мин
Отклонение выборочной средней от генеральной с вероятностью 99% составит: 
мин
Доверительный интервал для мужчин: 
;
Определяем доверительный интервал для женщин.
n=192; =10 мин; xср=210 мин.
Определим скорректированную дисперсию: ;
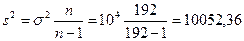
Средняя ошибка выборки: 
мин
Отклонение выборочной средней от генеральной с вероятностью 99% составит: 
мин
Доверительный интервал для женщин: 
;
Интервал для разности значений среднего времени, затрачиваемого женщинами и мужчинами на домашние работы: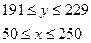 
. Из данных интервалов видно, что женщины затрачивают на домашние работы от 3 часов 11 минут до 3 часов 49 минут, а мужчины от 1 часа 20 минут до 4 часов 10 минут. Но в целом женщины затрачивают времени больше.
Тема 8. Анализ рядов динамики
Задание 1.
Таблица 8.1
| Месяц | ||||||||||||
| Товарооборот, млн. руб. | 25,7 | 25,9 | 26,6 | 26,3 | 26,4 | 26,9 | 26,7 | 26,8 | 26,7 | 26,8 | 26,3 | 27,1 |
| Цепной абсолютный прирост, млн. руб. в месяц | - | 0,2 | 0,7 | -0,3 | 0,1 | 0,5 | -0,2 | 0,1 | -0,1 | 0,1 | -0,5 | 0,8 |
| Базисный абсолютный прирост, млн. руб. в месяц | - | 0,2 | 0,9 | 0,6 | 0,7 | 1,2 | 1,1 | 1,1 | 0,6 | 1,4 | ||
| Темп роста цепной | - | 1,01 | 1,03 | 0,99 | 1,00 | 1,02 | 0,99 | 1,00 | 1,00 | 1,00 | 0,98 | 1,03 |
| Темп роста базисный | - | 1,01 | 1,04 | 1,02 | 1,03 | 1,05 | 1,04 | 1,04 | 1,04 | 1,04 | 1,02 | 1,05 |
| Темп прироста | - | 0,01 | 0,04 | 0,02 | 0,03 | 0,05 | 0,04 | 0,04 | 0,04 | 0,04 | 0,02 | 0,05 |
| Средний товарооборот за месяц, млн. руб. | 0,83 | 0,93 | 0,86 | 0,88 | 0,85 | 0,90 | 0,86 | 0,86 | 0,89 | 0,86 | 0,88 | 0,87 |
Цепной абсолютный прирост: 
;
Базисный абсолютный прирост: 
;
Цепной темп роста: 
;
Базисный темп роста: 
;
Темп прироста: 
;
Средний темп роста определяется как геометрическая средняя из цепных темпов роста за 12 месяцев или из общего (базисного) темпа роста за 12 месяцев:
.
Вывод: рассматривая базисный абсолютный ежемесячный прирост товарооборота можно сделать вывод о том, что наблюдается постоянное увеличение товарооборота, наибольший прирост был в декабре (на 1,4 млн. руб.). Рассматривая цепной абсолютный прирост, можно отметить его непостоянство, т.е. в 4-х месяцах 1999 года товарооборот снижался относительно предыдущего месяца. Темп прироста в нашем случае получился всегда положительным.
Задание 2.
Для определения формы тренда и расчета его параметров составляется вспомогательная таблица.
Таблица 8.2
Расчет параметров тренда
| Месяц | Товарооборот yi, млн. руб. | ti | t2 | yi ti | Уровни трендов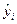 
| Индекс сезонности ii,сез,% |
| 25,7 | -11 | -282,7 | 26,07 | 96,90 | ||
| 25,9 | -9 | -233,1 | 26,15 | 97,66 | ||
| 26,6 | -7 | -186,2 | 26,23 | 100,30 | ||
| 26,3 | -5 | -131,5 | 26,31 | 99,17 | ||
| 26,4 | -3 | -79,2 | 26,39 | 99,54 | ||
| 26,9 | -1 | -26,9 | 26,48 | 101,43 | ||
| 26,7 | 26,7 | 26,56 | 100,67 | |||
| 26,8 | 80,4 | 26,64 | 101,05 | |||
| 26,7 | 133,5 | 26,72 | 100,67 | |||
| 26,8 | 187,6 | 26,80 | 101,05 | |||
| 26,3 | 236,7 | 26,88 | 99,17 | |||
| 27,1 | 298,1 | 26,97 | 102,18 | |||
| Итого | 318,2 | 23,4 | 318,20 |
Чаще всего при выравнивании используется линейная зависимость:
;
Линейная зависимость выбирается в тех случаях, когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные и цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению.
Для нахождения аo и а1 используется система нормальных уравнений:
, откуда 
и 
.
; 
.
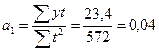Модель тренда имеет вид: 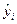= 26,52+0,04t.
Для прогноза товарооборота на июль и ноябрь 2000 года с учетом сезонных колебаний необходимо найти индекс сезонности: 
,
где 
- уровень показателя за месяц;
- общий уровень показателя.
млн. руб., где d – количество дней в месяце.
Прогноз товарооборота в июле и ноябре 2000 года по уравнению прямой линии: 
= 26,52+0,04*25=27,52 млн. руб.;
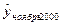= 26,52+0,04*33=27,84 млн. руб.
С учетом сезонных колебаний:
= 27,28*1,0067=27,70 млн. руб.;
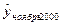= 27,44*0,9917=27,60 млн. руб.
Рис. 8.1. Кривая товарооборота за год и ее выравнивание
Задание 3.
Таблица 8.3
| Год | Введенная жилая площадь, тыс. м2 | Темпы роста | ||
| Базисный | Цепной | Средний | ||
| - | - | 1,004556 | ||
| 1,0370 | 1,0370 | |||
| 1,0370 | 1,0000 | |||
| 1,0370 | 1,0000 | |||
| 1,1111 | 1,0714 | |||
| 1,1481 | 1,0333 | |||
| 1,0370 | 0,9032 | |||
| 1,0370 | 1,0000 |
Средний темп роста определяется как геометрическая средняя из цепных темпов роста за 8 лет (с 1992 по 1999) или из общего (базисного) темпа роста за 8 лет:
.
Для определения формы тренда и расчета его параметров составляется вспомогательная таблица.
Таблица 8.4
| Год | Введенная жилая площадь yi, тыс. м2 | ti | t2i | yi ti | Уровни тренда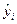
| |
| -7 | -189 | 27,75 | ||||
| -5 | -140 | 27,96 | ||||
| -3 | -84 | 28,18 | ||||
| -1 | -28 | 28,39 | ||||
| 28,61 | ||||||
| 28,82 | ||||||
| 29,04 | ||||||
| 29,25 | ||||||
| Итого |
Чаще всего при выравнивании используется линейная зависимость:
;
Линейная зависимость выбирается в тех случаях, когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные и цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению.
Для нахождения аo и а1 используется система нормальных уравнений:
, откуда и .
; 
.
Модель тренда имеет вид: 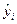= 28,5+0,1071t.
Точечный прогноз на 2000 год составит: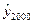 
= 28,5+0,1071*9=29,46 тыс. м2
