Задание 1.
Таблица 6.1
| Размер |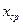 
| ||||||
| Магазин №1 | 16.67 | ||||||
| Магазин №2 | 13.33 | ||||||
| Магазин №3 | 18.33 | ||||||
| Обшее кол-во | 48.33 |
Рис. 6.1.1. Гистограммы распределений размеров кроссовок для каждого магазина и суммарная
Рис.6.1.2. Полигоны распределений размеров кроссовок для каждого магазина и суммарная
Дисперсия, или средний квадрат отклонения (обозначим σ2) есть средняя арифметическая из квадратов отклонений вариант от их средней арифметической, т. е. в математической записи
где xi-варианта с порядковым номером i;
- средняя арифметическая;
n – численность совокупности.
Групповая дисперсия (по каждому магазину):
;
;
.
Межгрупповая дисперсия:
;
;
.
Общая дисперсия:
.
Коэффициент вариации (обозначим V) представляет собой отношение среднего квадратичного отклонения к средней арифметической, выраженное в процентах, т. е.
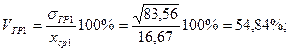
Модой (обозначим Мо) называется варианта, наиболее часто встречающаяся в данном вариационном ряду. Для дискретного ряда мода равна варианте с наибольшей частотой или частостью. В нашем случае наиболее часто встречаются кроссовки 43 размера (97 раз), т.е. Мо=43.
Медианой (обозначим Mе) называется такое значение варьирующего признака, которое приходится на середину вариационного ряда.
При нахождении медианы дискретного вариационного ряда могут возникнуть два случая: 1) число вариант нечетно (k=2m+1), 2) число вариант четно (k=2m). В первом случае Me=xm+1, т. е. медиана равна центральной (срединной) варианте ряда, во втором случае Me=(xm+xm+1)/2, т.е. медиана принимается равной полу сумме находящихся в середине ряда вариант.
В нашем случае число вариант – 6, значит 6=2m, m=3.
Медиана суммарного распределения равна:
Me=(xm+xm+1)/2=(40+42)/2=41.
Вывод: самым ходовым размером является 43. Его продажи были максимальны как в целом по магазинам, так и в частности по каждому магазину. Меньше всего продали кроссовок 40 размера в общем по магазинам, но если рассматривать каждый магазин в отдельности, то менее ходовым являются размеры 40,41 и 45. Среднее количество продаж кроссовок по размерам составляет: магазин № 1 – 16,67; магазин № 2 – 13,33; магазин № 3 – 18,33 и общее по магазинам – 48,33. Вероятность продажи среднего числа кроссовок по размерам для магазина № 1 составляет 55%, магазина № 2 – 46 %, магазина № 3 – 58% и общего среднего для всех магазинов – 48%. Мода соответствует 43 размеру кроссовок. Медиана суммарного распределения равна 41.
Задание 2.
Таблица 6.2
| Среднедушевой доход в месяц, руб. | Чис-лен-ность насе-ления, f | Сере-дины интер-валов, x | Интер-вальная разность, h | Накоп-ленная часто-та | Плот-ность интер-вала | x*f | 
|
| до 400 | 0.17 | 10370175.62 | |||||
| 400-600 | 0.105 | 2606017.56 | |||||
| 600-800 | 0.085 | 394178.72 | |||||
| 800-1000 | 0.135 | 61503.10 | |||||
| 1000-1200 | 0.03 | 368212.81 | |||||
| 1200-1600 | 0.0225 | 2700046.49 | |||||
| 1600-2000 | 0.02 | 7185495.87 | |||||
| свыше 2000 | 0.025 | 18163688.02 | |||||
| Сумма | 41849318.18 |
Средняя арифметическая интервального вариационного ряда вычисляется следующим образом: за значение признака принимается середина интервала (центральное значение), которая рассчитывается как арифметическая средняя границ интервала. Часто вычисление средней арифметической для интервального вариационного ряда осложняется тем, что неизвестны или нижняя граница первого интервала, или верхняя граница последнего интервала, или та и другая одновременно. В таких случаях условно предполагают, что интервальная разность неопределенного интервала такая же, что и у рядом стоящего, и на основе этого предположения устанавливают границы крайних интервалов.
Среднедушевой доход: 
(руб.).
Медианой (обозначим Mе) называется такое значение варьирующего признака, которое приходится на середину вариационного ряда. Для интервального вариационного ряда медиана вычисляется по формуле:
,
где xMe(min) - нижняя граница медианного интервала;
h - величина этого интервала, или интервальная разность;
fi- частоты или частости;
k – число вариант;
- накопленная сверху частота (или частость) интервала, предшествующего медианному;
- частота или частость медианного интервала.
Вычисление медианы начинается с нахождения интервала, содержащего медиану. Медианному интервалу соответствует первая из накопленных частот или частостей, превышающая половину всего объема совокупности. В нашем случае объем совокупности равен 132, первая из накопленных частостей, превышающая половину всего объема совокупности, - 72 (см. табл. 6.2). Следовательно, интервал 600-800 будет медианным. Далее, xme(min)=600, h=200, =55, fMe=17.
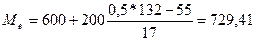(руб.).
Модой (обозначим Мо) называется варианта, наиболее часто встречающаяся в данном вариационном ряду. Для интервального вариационного ряда модальный интервал, т. е. интервал, содержащий моду, определяется по наибольшей частоте (частости) в случае равных интервалов и по наибольшей плотности в случае неравных интервалов. Значение варианты, равное моде, отыскивается приближенными методами. Довольно грубое приближение можно получить, взяв за моду центральное значение модального интервала, т. е. среднее арифметическое границ интервала. Из таблицы 6.2 видно, что наибольшая плотность населения соответствует интервалу интервалу 200-400. Это и есть модальный интервал. Рассчитываем моду: Mo=(200+400)/2=300 (руб.).
Дисперсия, или средний квадрат отклонения (обозначим σ2) есть средняя арифметическая из квадратов отклонений вариант от их средней арифметической, т. е. в математической записи
,
где xi-варианта с порядковым номером i;
- средняя арифметическая;
k- число вариант;
fi - частота или частость с порядковым номером i.
Часто для исследования удобно представлять меру рассеяния в тех же единицах измерения, что и варианты. Тогда вместо дисперсии используют среднее квадратичное отклонение, которое является квадратным корнем из дисперсии, т. е. среднее квадратичное отклонение вычисляется по формуле
.
Коэффициент вариации (обозначим V) представляет собой отношение среднего квадратичного отклонения к средней арифметической, выраженное в процентах, т. е.
Коэффициент вариации позволяет: 1) сравнивать вариацию одного и того же признака у разных групп объектов; 2) выявить степень различия одного и того же признака у одной и той же группы объектов в разное время; 3) сопоставить вариацию разных признаков у одних и тех же групп объектов.
Квартильный коэффициент дифференциации показывает, во сколько раз минимальные доходы 25% самого богатого населения превышает максимальные доходы 25% наименее обеспеченного населения:
где 
и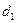 
- соответственно четвертый и первый квартили.
Когда значение находится в зоне, где расположено менее 25% наблюдаемых значений переменной, то говорят, что оно расположено в нижнем квартиле ().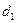
Если же оно расположено там, где находятся верхние 25% значений, то говорят, что оно расположено в верхнем квартиле (). При помощи программы Microsoft Office Excel и встроенного в него пакета анализа определяем квартили доходов населения по серединам интервалов (x): 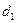= 650 (руб.), = 2200 (руб.).
.
Гистограмма распределения применяется для изображения интервального ряда. Для построения гистограммы на горизонтальной оси откладывают последовательно отрезки, равные интервалам признака, и на этих отрезках, как на основаниях, строят прямоугольники, высоты которых равны частотам.
Кумулята есть графическое изображение вариационного ряда, когда на вертикальной оси откладываются накопленные частоты или частности, а на горизонтальной - значения признака. Кумулята служит для графического представления как дискретных, так и интервальных вариационных рядов.
Рис. 6.2.1. Гистограмма распределения доходов населения
Рис. 6.2.2. Кумулята распределения доходов населения
