Любое дифференциальное уравнение первого порядка, разрешенное относительно старшей производной, можно записать в виде
.
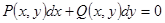Если выполнено соотношение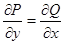 
, то уравнение называется уравнением в полных дифференциалах.
Причину такого названия понять легко. Пусть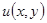 
- функция двух переменных, дифференцируемая и имеющая непрерывные вторые частные производные по своим переменным. Тогда 
.
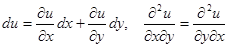Если обозначить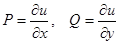 
, то исходное уравнение можно записать в виде полного дифференциала
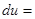
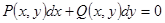, а соотношение 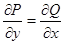как раз и означает равенство смешанных производных 
.
Поэтому решить уравнение в полных дифференциалах – означает найти функцию 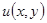(она называется потенциалом). Так как 
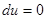на решениях дифференциального уравнения, то потенциал будет первым интегралом исходного дифференциального уравнения:
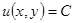
Для решения уравнения в полных дифференциалах можно использовать два способа.
1) 
,
+ 
.
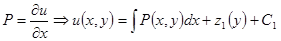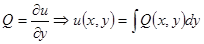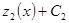Здесь интегрирование ведется «частным образом»: только по переменной x, считая y константой или только по y, считая x константой.
Сравнивая оба выражения для 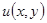, находим функции 
и константы.
Если какой-либо из интегралов, например,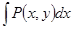 
не берется или его вычислить сложно, то можно найти + .
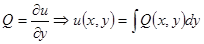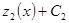Затем, дифференцируя 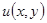частным образом по x, надо сравнить 
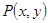с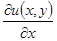 
и определить функции и константы.
2) Потенциал можно определять по формуле (она будет выведена из независимости криволинейного интеграла от пути интегрирования позже, в 3 семестре)
. 
.
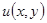
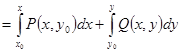Пример. 
.
Решим уравнение первым способом.
Так как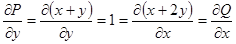 
, то это – уравнение в полных дифференциалах.
,
.
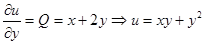
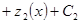Сравнивая оба равенства, видим, что 
, поэтому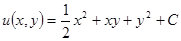 
. Соотношение 
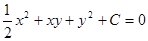- это первый интеграл заданного дифференциального уравнения.
Решим уравнение вторым способом.
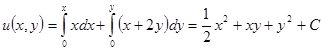. Здесь принято 
.
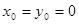Интегрирующий множитель.
Можно поставить вопрос, нельзя ли любое дифференциальное уравнение первого порядка свести к уравнению в полных дифференциалах?
Оказывается, что существует такой интегрирующий множитель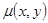 
, умножая на который обе части любого дифференциального уравнения, удовлетворяющего условиям теоремы Коши, можно привести это уравнение к уравнению в полных дифференциалах.
Однако неясно, как в общем случае найти этот интегрирующий множитель. Ясно только, что он должен удовлетворять уравнению
.
Оказывается, если 
(является функций только одной переменной x), то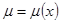 
. Если 
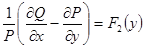(является функций только одной переменной y), то 
.
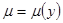Пример.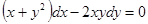 
.
Покажите, что здесь выполняется первое условие и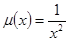 
.
Найдите потенциал, покажите, что он равен 
.
Лекция 13. Геометрическая интерпретация дифференциальных
