Полином 
– знаменатель рациональной дроби может иметь действительный корень 
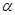некоторой 
- ой кратности. Тогда 
, где многочлен 
уже не имеет корня 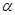. В этом случае из рациональной дроби можно выделить элементарную рациональную дробь вида 
.
Лемма 2. Пусть 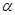- действительный корень - ой кратности полинома – знаменателя рациональной дроби. Тогда
= 
, где многочлен уже не имеет корня .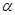
Доказательство. Приведем дроби к общему знаменателю и приравняем числители полученных дробей.
. Тогда выражение 
должно делиться на 
, т.е. 
. Этого можно добиться, выбрав 
.
Следствие 1. В условиях леммы 2 рациональную дробь можно представить в виде
где 
не имеет корня .
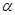Доказательство. Применим лемму 2 раз и получим указанное разложение.
Полином – знаменатель рациональной дроби может иметь пару комплексно сопряженных корней 
- ой кратности. Тогда 
Причем уже не являются корнями полинома . В этом случае из рациональной дроби тоже можно выделить некоторую элементарную рациональную дробь вида 
.
Лемма 3. Пусть – знаменатель рациональной дроби имеет пару комплексно сопряженных корней - ой кратности. Тогда рациональную дробь можно представить в виде
= 
, где уже не являются корнями полинома .
Доказательство. Приведем дроби к общему знаменателю и приравняем числители полученных дробей.
= 
. 
должно делиться как на 
, так и на 
. Поэтому
, где =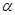 
, 
= 
Отсюда имеем систему уравнений для определения констант 
.
Определитель этой системы равен 
, так как корни комплексные и 
. Поэтому система имеет единственное решение.
Следствие 2. В условиях леммы 2 рациональную дробь можно представить в виде
= 
+ 
+ …+ 
+ 
,
где уже не являются корнями полинома 
.
Доказательство. Применяем лемму 3 нужное число раз и получаем искомое разложение.
Теорема. Рациональная функция может быть представлена в виде
= 
+ 
+…+ 
+…+ + + …+ + …+ 
,
где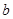 
- простой действительный корень , 
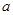- действительный корень кратности , 
- пара комплексно сопряженных корней кратности (комплексно сопряженные корни 
), 
- простая пара комплексно сопряженных корней (корни 
).
Доказательство. Применяем к рациональной функции лемму 1, выделяем полином – целую часть , затем по лемме 2, выделяем члены разложения, соответствующие простым и кратным действительным корням. Затем по лемме 3 выделяем члены разложения, соответствующие простым и кратным парам комплексно сопряженных корней. Так как многочлен может иметь корни лишь перечисленных типов, то разложение этим и исчерпывается.
Следствие 3. Задача интегрирования рациональной функции сводится к задачам интегрирования элементарных рациональных дробей четырех типов
1) 
, 2) 
, 3) , 4) 
.
