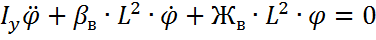Железнодорожный путь не является строго прямолинейным в плане и имеет различные неровности и искривления. Указанные неровности и искривления могут быть преднамеренными т.е. обьективно полезными (кривые и стрелки),и случайными (вредными), допущенными при укладке и ремонте пути. В случае притяжения гребня колеса к рельсу в принципе возможны 2 причины последующего схода колесной пары (кп) с рельсов: её статическое выжимание из рельсовой колеи боковыми силами и выкатывания гребня колеса на рельс. Схема действия сил на кп показана на рисунке. Со стороны вагона на кп при её статич. Выжимании действуют Р1,Р2 и F,со стороны рельсов – нормальные реакции N и Р2, а также силы трения в точках контакта от этих реакций Nµ и P2µ, где µ- коэф-ент трения скольжения между(м/у) колесами и рельсами. Направления сил трения выбрано противоположно направлению скольжения точек контакта колеса и рельса при выжим. кп. В проекциях на касательную к точке контакта гребня колеса с рельсом τ-это условие вырожается в виде неравенства
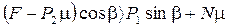 (1) Величину N можно определить из условия рановесия кп, проектируя все силы на нормаль n:
(1) Величину N можно определить из условия рановесия кп, проектируя все силы на нормаль n:
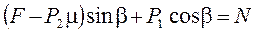 (2) После преобразования получим, что кп выжимается из колеи:
(2) После преобразования получим, что кп выжимается из колеи:
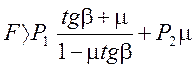 (3)
(3)
Как видно из полученных выражений возможность выжимания не только нагрузками действующими на кп, но и значениями µ и β. В частности, при Р1>0, µ≈0,4, β≈70˚ выжимание становится невозможным. С другой стороны, указанная возможность сильно зависит от степени вертикальной обезгрузки набегающего колеса. Гребень этого колеса совершенно перестаёт препятствовать выжиманию кп из рельсовой колеи при Р1≈0.
Вырожение 3 получено в предположении статического действия нагрузок, приложенных к кп. В эксплуатационных условиях указанные нагрузки могут менять свою величину, и промежуток времени, в течении которого выполняется условие 3, может оказаться недостаточным для предооления инерции кп при её выжимании из рельсовой колеи.Время в течении которого гребень кп успевает взобратся на рельс
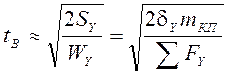 (4)
(4)
Sy- боковое смещение кп, Wy-горизонтальная составляющая центра кп,
Mrg- масса кп,∑Fy- сумма горизонтальных проекций сил.Преобразуем (4) 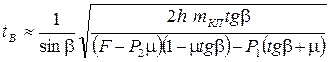 (5)
(5)
Это формула может быть использована для определения условий, при которых кп выжимается из колеи в случае действия на неё кратковременных динамических нагрузок.
Обозначая фактическую длительность действия таких нагрузок t и принимая t≥tВ , указанные условия можно записать в виде неравенства
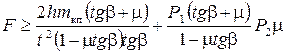 (6)
(6)
условие 6 учитывает инертность кп
Указанные условия существенно зависят от угла нклона гребня колеса β и коэ-та трения м/у колёсами и рельсами µ
40. Составление дифференциальных уравнений собственных колебаний кузова вагона (галопирование, h = 0) (По Лагранжу)
Галопирование - это колебания по оси Y.
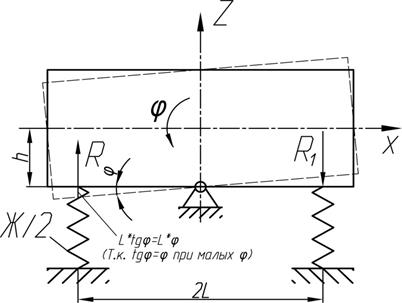 m – масса кузова;
m – масса кузова;
Ix, Iy, Iz – моменты инерции кузова относительно его центральных осей;
ЖВ, Жг – вертикальная и поперечная жесткость рессорного подвешивания;
βВ, βг – суммарные коэффициенты демпфирования подвешивания вагона в вертикальном и поперечном направлениях;
2L, 2B – база вагона и расстояние между вертикальными и горизонтальными комплектами поперек вагона;
h – высота расположения центра тяжести кузова от уровня горизонтальных упруговязких связей;
fCT – статический прогиб рессорного подвешивания вагона;
Для составления дифференциального уравнений используем уравнения Лагранжа 2 рода:
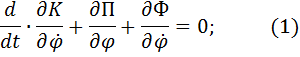
где t – время; К, П – кинетическая и потенциальная энергия системы;
Ф – функция рассеивания; φ –обобщенная координата.
Кинетическая энергия рассматриваемой механической системы, включающей в себя одно жёсткое тело (кузов), 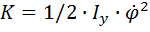 , где
, где 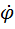 – координата центра тяжести кузова. Дифференцируя получим
– координата центра тяжести кузова. Дифференцируя получим 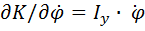 ;
;
Дифференцируя по времени получим 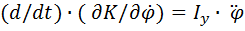 . (2)
. (2)
Потенциальная энергия системы вертикальных упругих элементов:
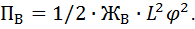 Дифференцируя получим
Дифференцируя получим 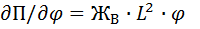 (3) Функция рассеивания представляет собой мощность, развиваемую силами неупругого сопротивления и выражается
(3) Функция рассеивания представляет собой мощность, развиваемую силами неупругого сопротивления и выражается 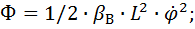 Дифференцируя получим
Дифференцируя получим 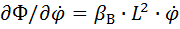 (4)
(4)
Подставляем значения производных (2), (3), (4) в уравнение (1)
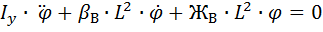
40 Составление дифференциальных уравнений собственных колебаний кузова вагона (Галопирование, h=0) (По Даламберу)
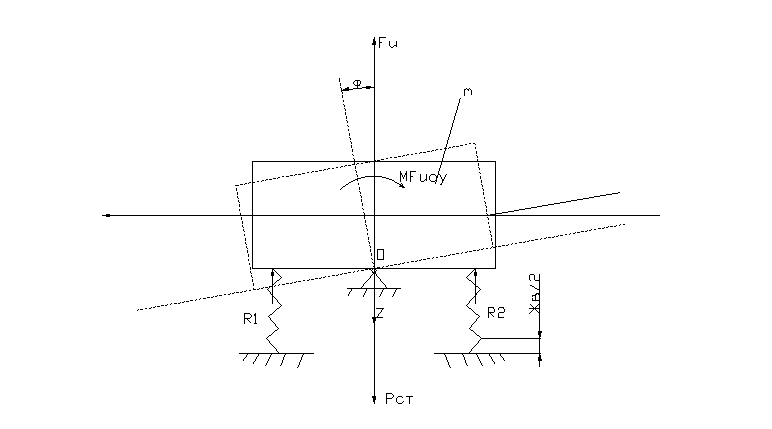 φ – определение положения кузова
φ – определение положения кузова
Тогда по уравнению Даламбера (аналитический вид):

Моменты от приложенных сил равны нулю: 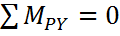
Моменты от сил реакции опоры:
– от упругой связи (пружины) – 
– от линейной или вязкой связи (гидравлическ. гаситель колебаний) – 

Моменты от сил инерции: 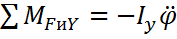
Тогда
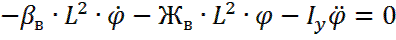
Получим ДУ собственных колебаний кузова вагона при галопирование (h=0)