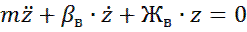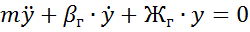Для представления вагона в качестве механической системы с конечным числом степеней свободы его разбивают на твердые тела и связи. Если число степеней свободы не велико, ММ получаем с помощью уравнения Даламбера в декартовых координатах.
Так как виляния – это колебания вокруг оси Z, то расчётная схема будет выглядеть следующим образом:
Для составления дифференциального уравнения собственных колебаний воспользуемся принципом Даламбера. Уравнение движения тела в Декартовых координатах имеет вид:
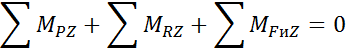
Моменты от заданных сил равны нулю: 
Моменты от сил реакции опоры:
– от упругой связи (пружины) – 
– от линейной или вязкой связи (гидравлич. гаситель колебаний) –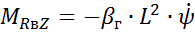 
Моменты от сил инерции:
Тогда
Получим ДУ собственных колебаний кузова вагона при вилянии
30. Устойчивость колёсной пары при движении в рельсовой колее. Вкатывание колеса гребнем на рельс.
Когда колесо катится по рельсу без взаимного проскальзывания их поверхностей катания, мгновенный центр скоростей располагается в точке контакта этих поверхностей. Гребень колеса, набегая на рельс, скользит по нему, воспринимая нормальную реакцию со стороны рельса и силу трения, противоположную скорости скольжения. Вертикальные составляющие указанных сил разгружают поверхности катания колеса и рельса, и уменьшают сцепление между ними в точке контакта. При некотором значении боковой нагрузки F, действующей на кол. пару, поверхности катания колеса и рельса обезгруживаются. В рез-те колесо начинает катиться конической поверхностью гребня по кромке направляющего сечения рельса, не соскальзывая вниз, и если угол набегания гребня кол. пары на рельс остается полож-ым, а изменение сил, действующих на колесо, не вызовет нарушения сцепления в новой точке контакта, то такое качение приведет к вкатыванию гребня колеса на пов-ть катания рельса и последующему сходу кол. пары с рельсов.
Условие, при к-ом осущ-ся перекатывание конической пов-ти гребня колеса по кромке направляющего сечения рельса, м. б. получено аналогично выражению
F > P1 (tgβ + µ)/(1 - µtgβ) + P2µ (0)
с помощью расчетной схемы, приведенной на рис. На этой схеме направление сил трения Nµ и P2µ выбрано противоположным направлению соскальзывания кол. пары внутрь колеи. В рез-те получаем:
F ≥ P1 (tgβ - µ)/(1 + µtgβ) – P2µ (1)
Для тех же типичных условий движения (при P1 = 0,6P, P2 = 0,4P, β = 60˚, µ = 0,3) использование выр-ия (1) приводит к рез-ту F ≥ 0,45P.
Как видно из приведенных расчетов, вкатывание колеса гребнем на рельс яв-ся более опасным по сравнению с выжиманием кол. пары из колеи поперечными силами.
Для того чтобы гребень колеса успел вкатиться на рельс, условие (1) должно выполняться в течение некоторого промежутка времени tсх, достаточного для такого вкатывания. Это время м. опр-ть, разделив боковое перемещение кол. пары, получаемое ею в процессе вкатывания гребня и равное h / tgβ, на скорость этого перемещения v tgα (где v – скорость движения вагона):
t > tсх ≈ h /(v·tgα·tgβ) (2)
При h = 18 мм, v = 30 м/с (108 км/ч), tgα = 0,02, β = 60˚ значение tсх по ф-ле (2) равно 0,017 с. Следует отметить, что с увел-ем скорости дв-ия вел-на tсх уменьа-ся. Это повышает опасность схода кол. пары с рельсов за счет увел-ия вероятности возникновения необходимых для этого условий. Аналогичный вывод д. б. сделан и в отношении угла набегания кол. пары на рельсы.
Подводя итог изложенному выше, м. сделать вывод о том, что устойчивость дв-ия кол. пары по рельсам нарушается в случае возникновения условий (1) и (2) при полож-х значениях этого угла. В силовом отношении условие (1) яв-ся более жестким (выполняющимся при меньшем значении боковой нагрузки) по сравнению с условием (0). Тем не менее, это не исключает возможности схода кол. пары с рельсов в рез-те ее выжимания из колеи в некоторых достаточно обычных эксплуатационных условиях (при отрицательных или малых углах набегания, импульсивном действии боковых нагрузок - например, при прохождения стрелок или ударном входе в кривую, низких значениях коэф-та трения между колёсами и рельсами).
С практической точки зрения гораздо удобнее пользоваться критерием, который определял бы степень устойчивости движения колесных пар вагона по рельсовому пути. Для. выработки такого приближённого критерия можно использовать условие (1), представив его со знаком равенства в виде:
(F + P2µ / P1)кр = tgβ - µ / 1+ µtgβ, (3)
где [(F+P2µ) / P1]кр критическоезначение соотношения действующих на колесную пару сил, соответствующее появлению опасности её схода с рельсов.
Когда фактическое соотношение сил [(F+P2µ) / P1]фак ниже критического, то опасности схода не существует. В качестве количественного критерии степени усто11чивости движения колеегюй пиры вагона по рельсам может быть принят гак называемый коэффициент запаса устойчивости против ее схода с рельсов:
Ky = (F + P2µ / P1)кр: (F+P2µ / P1)фак = tgβ - µ / 1+ µtgβ(P1/F + P2µ)фак (4)
Для надёжного обеспечения устойчивости движения колёсной пары значение Ку, должно быть больше единицы. Если это требование не выполняется, то для реализации устойчивости необходимо убедиться в не возможности возникновения условий (0) и (1) с учётом длительности действия нагрузок и фактического значения угла набегания αфак.
Схема сил, действующих на кол. пару при вкатывании гребня колеса на рельс.
31Вывод ММ колебаний (подпрыгивание, h=0) (По Даламберу)
Получение ММ колебаний одномассовой мех.системы по след.расчётной схеме:
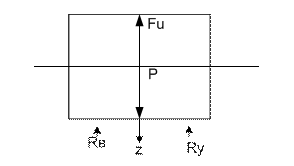
Движение груза массой m ограничено упруго-вязкой связью с жёсткостью и коэффициент демпфирования β, z – обобщённая координата.
Тогда по уравнению Даламбера (аналитический вид):
Заданные силы равны: 
Силы реакции опоры:
– от упругой связи (пружины) – 
– от линейной или вязкой связи (гидравлических гаситель колебаний) – 
Силы инерции: 
Тогда
Получим ДУ собственных колебаний кузова вагона при подпрыгивании, h=0
