Рассмотрим систему в виде невесомой балки с сосредоточенной массой m, горизонтальным перемещением и поворотом которого будем пренебрегать. При таких предпосылках единственная материальная точка, т.е. сосредоточенная масса величиной m может совершать перемещения только в вертикальном направлении, следовательно, система имеет одну степень свободы.
Будем исследовать движение системы из ее исходного положения равновесия при t = 0 (рис.14.1, а), считая перемещение вниз положительным.
Пусть на балку действует динамическая сила величиной: 
, где 
частота вынуждающей силы. Обозначая дополнительное перемещение массы m от динамических нагрузок через y (t), вводим следующие начальные условия:
; 
.
В процессе движения на массу действует сила инерции 
и сила сопротивления по Фойхту 
. Сила сопротивления движению возникает от различных внешних и внутренних причин: сопротивление движению внешней среды, трение в местах соединения элементов и опорных частях, внутреннее неупругое сопротивление материалов конструкций и т.д.
Заметим, что система, обладающая свойствами внутреннего сопротивления называется консервативной, а система, лишенная данного свойства неконсервативной.
Вводим следующие обозначения: 
вертикальное перемещение балки в точке закрепления массы m от действия вертикальной единичной силы Р = 1, приложенной в той же точке; 
вертикальное перемещение балки в точке закрепления массы m от динамической силы 
, при этом: 
; 
вертикальное перемещение балки в точке закрепления массы от действия вертикальной единичной силы Р = 1, приложенной в точке приложения внешней силы при ее отсутствии.
Применяя метод суперпозиции, очевидно, что, в произвольный момент времени полное перемещение сосредоточенной массы m принимает значение:
,
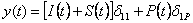откуда и определяется дифференциальное уравнение движения рассматриваемой системы:
Принимаем обозначения: 
круговая частота собственных колебаний системы; 
коэффициент затухания.
С учетом введенных обозначений, уравнение движения системы (14.3) принимает вид:
. Решение дифференциального уравнения (14.4), с учетом начальных условий (14.1) и, учитывая, что для реальных конструкций всегда выполняется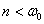 
, записывается в виде:
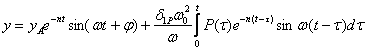
Здесь приняты следующие обозначения:
; 
; 
.
Круговая частота 
называется круговой частотой собственных колебаний системы с учетом сил затухания.
Коэффициент затухания колебания определяется по корректированной гипотезе Фойхта, позволяющей получить наиболее обоснованные результаты для учета диссипации энергии в системе в процессе колебаний, т.е.:
,
где 
называется логарифмическим декрементом затухания и определяется через отношения соседних амплитуд колебания, возникающих через промежуток времени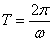 
:
.
Для различных конструкций средние значения приводятся в таблице 14.1.
Выражение (14.5) определяет перемещение сосредоточенной массы при действии силы , изменяющейся во времени по произвольному закону. Первый член выражения характеризует собственные колебания системы, а второй, интегральный член вынужденные колебания.
Так как 
, то решение (14.5) преобразуется и принимает вид:
.
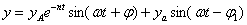Здесь приняты следующие обозначения:
; 
; 
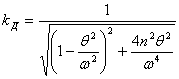. (14.10)
Если в момент времени t = 0 система находится в состоянии покоя, т.е. 
, то решение (14.9) с учетом (14.10) преобразуется в виде:
.
Величина kД называется коэффициентом динамичности и характеризует эффект от динамической нагрузки по отношению к аналогичной статической нагрузке величиной P(t) = P0 = const.
Коэффициент динамичности существенно зависит от отношения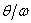 
. При 
коэффициент динамичности стремится принять максимальное значение и колебания системы при 
называются резонансными, а амплитуда колебаний принимает опасное значение:
.
