1. Привести уравнения кривых к каноническому виду и построить линии, определяемые уравнениями:
1)  ;
;
2) 
3) 
4) 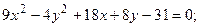
5) 
6) 
Ответы:
1) 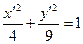 , новое начало
, новое начало 
2) 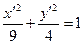 , новое начало
, новое начало 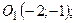
3)  , новое начало
, новое начало 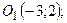
4) 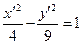 , новое начало
, новое начало 
5) 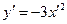 ; новое начало
; новое начало 
6) 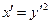 ; новое начало
; новое начало  .
.
2. Привести уравнения кривых к каноническому виду и построить линии, определяемые уравнениями:
1) 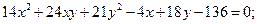
2) 
Ответы:
1) 
2)  .
.
ТИПОВЫЕ РАСЧЕТЫ
Типовые расчеты – это самостоятельные домашние работы, которые выполняются студентом после изучения отдельных частей курса высшей математики. Типовые расчеты являются подготовкой к зачетной контрольной работе.
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ
ТИПОВЫХ РАСЧЕТОВ
При выполнении типовых расчетов требуется строгое соблюдение указанных ниже правил.
1. Работа выполняется в тетради в клетку чернилами любого цвета кроме красного. Необходимо оставлять поля для замечаний преподавателя.
2. В работу включаются все задачи, указанные в задании, и строго по положенному варианту.
3. Решения задач располагаются в порядке возрастания их номеров, указанных в задании, сохраняя номера задач.
4. Условия задач приводятся полностью. Решения излагаются подробно и аккуратно, объясняются все действия по ходу решения и делаются необходимые чертежи.
5. Вариант выбирается в соответствии с порядковым номером студента в списке группы.
6. После получения проверенной работы исправляются все отмеченные ошибки и работа сдается на повторную проверку.
МАТРИЦЫ. ОПРЕДЕЛИТЕЛИ.
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Задание 1. Решить систему уравнений: 1) методом Гаусса; 2) по правилу Крамера, с помощью обратной матрицы
1.1.
1)  2)
2) 

1.2.
1)  2)
2) 
1.4.
1)  2)
2) 
1.5.
1)  2)
2) 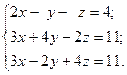
1.6.
1)  2)
2) 
1.7.
1)  2)
2) 
1.8.
1)  2)
2) 
1.9.
1)  2)
2) 
1.10
1)  2)
2) 
1.11.
1)  2)
2) 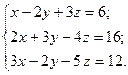
1.12.
1)  2)
2) 
1.13.
1)  2)
2) 
1.14.
1)  2)
2) 
1.15.
1)  2)
2) 
1.16.
1)  2)
2) 
1.17.
1)  2)
2) 
1.18.
1)  2)
2) 
1.19.
1)  2)
2) 
1.20.
1)  2)
2) 
1.21.
1)  2)
2) 
1.22.
1) 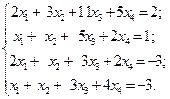 2)
2) 
1.23
1)  2)
2) 
1.24.
1) 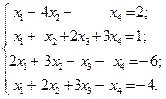 2)
2) 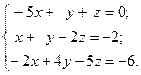
1.25.
1) 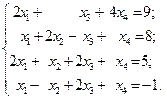 2)
2) 
1.26.
1)  2)
2) 
1.27.
1) 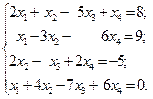 2)
2) 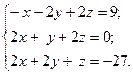
1.28.
1) 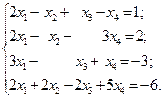 2)
2) 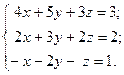
1.29.
1)  2)
2) 
1.30.
1)  2)
2) 
Задание 2. Найти значения матричного многочлена, если:
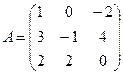 ;
;  ;
;
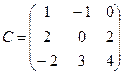 ;
; 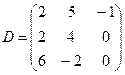 .
.
1.1.  1.16.
1.16. 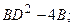
1.2.  1.17.
1.17. 
1.3.  1.18.
1.18. 
1.4.  1.19.
1.19. 
1.5.  1.20.
1.20. 
1.6.  1.21.
1.21. 
1.7. 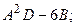 1.22.
1.22. 
1.8. 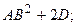 1.23.
1.23. 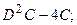
1.9.  1.24.
1.24. 
1.10.  1.25.
1.25. 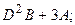
1.11.  1.26.
1.26. 
1.12.  1.27.
1.27. 
1.13.  1.28.
1.28. 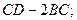
1.14. 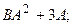 1.29.
1.29. 
1.15.  1.30.
1.30. 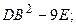
ВЕКТОРНАЯ АЛГЕБРА
Задание 1.. Написать разложение вектора x по векторам p, q, r. Координаты векторов приведены к таблице.
| №№ | х. | p | q | r |
| 1.1. | {-2, 4, 7} | {0, 1, 2} | {l, 0, 1} | {-l, 2, 4} |
| 1.2. | {6, 12, - 1} | {l, 3, 0} | {2, -1, 1} | {0, -1, 2} |
| 1.3. | {l, -4, 4} | {2, 1, -1} | {0, 3, 2} | {l, -1, 1} |
| 1.4. | {-9, 5, 5} | {4, 1, 1} | {2, 0, -3} | {-l, 2, 1} |
| 1.5. | {-5, -5, 5} | {-2, 0, 1} | {l, 3, -1} | {0, 4, 1} |
| 1.6. | {13, 2, 7} | {5, 1, 0} | {2, -1, 3} | {l, 0, -1} |
| 1.7. | {-19, -1, 7} | {0, 1, 1} | {-2, 0, 1} | {3, 1, 0} |
| 1.8. | {3, -3, 4} | {l, 0, 2} | {0, 1, 1} | {2, -1, 4} |
| 1.9. | {3, 3, -1} | {3, 1, 0} | {-l, 2, 1} | {-l, 0, 2} |
| 1.10. | {-1, 7, -4} | {-l, 2, 1} | {2, 0, 3} | {l, 1, -1} |
| 1.11. | {6, 5,-14} | {l, 1, 4} | {0, -3, 2} | {2, 1, -1} |
| 1.12. | {6, -1, 7} | {l. –2, 0} | {-l, 1, 3} | {l, 0, 4} |
| 1.13. | {5, 15, 0} | {l, 0, 5} | {-l, 3, 2} | {0, -1, 1} |
| 1.14. | {2, -1, 11} | {l, 1, 0} | {0, 1, -2} | {l, 0, 3} |
| 1.15. | {11, 5, -3} | {l, 0, 2} | {-l, 0, 1} | {2, 5, -3} |
| 1.16. | {8, 0, 5} | {2, 0, 1} | {l, 1, 0} | {4, 1, 2} |
| 1.17. | {3, 1, 8} | {0, 1, 3} | {l, 2, -1} | {2, 0, -1} |
| 1.18. | {8, 1, 12} | {l, 2, -1} | {3, 0, 2} | {-l, 1, 1} |
| 1.19. | {-9, -8, -3} | {l, 4, 1} | {-3, 2, 0} | {l, -1, 2} |
| 1.20. | {-5, 9, -13} | {0, 1, -2} | {3, -1, 1} | {4, 1, 0} |
| 1.21. | {-15, 5, 6} | {0, 5, 1} | {3, 2, -1} | {-l, 1, 0} |
| 1.22. | {8, 9, 4} | {l, 0, 1} | {0, -2, 1} | {l, 3, 0} |
| 1.23. | {23,-14,-30} | {2, 1, 0} | {l, -1, 0} | {-3, 2, 5} |
| 1.24. | {3, 1, 3} | {2, 1, 0} | {l, 0, 1} | {4, 2, 1} |
| 1.25. | {-l, 7, 0} | {0, 3, 1} | {l, -1, 2} | {2, -1, 0} |
| 1.26. | {11, -1, 4} | {l,-l, 2} | {3, 2, 0} | {-l, 1, 1} |
| 1.27. | {-13, 2, 18} | {l, 1, 4} | {-3, 0, 2} | {l, 2, -1} |
| 1.28. | {0, -8, 9} | {0, -2, 1} | {3, 1, -1} | {4, 0, 1} |
| 1.29. | {8, -7, -13} | {0, 1, 5} | {3, -1, 2} | {-l, 0, 1} |
| 1.30. | {2, 7, 5} | {l, 0, 1} | {l, -2, 0} | {0, 3, 1} |
Задание 2. Коллинеарны ли векторы с 1 и с 2, построенные по векторам a и b?
2.1. a ={1,-2,3}, b ={3,0,-1}, c 1=2 a +4 b, c 2=3 b - a.
2.2. a ={1,0,1}, b ={-2,3,5}, c 1= a +2 b, c 2=3 a - b.
2.3. a ={-2,4,1}, b ={1,-2,7}, c 1=5 a +3 b, c 2=2 a - b.
2.4. a ={1,2,-3}, b ={2,-1,-1}, c 1=4 a +3 b, c 2=8 a - b.
2.5. a ={3,5,4}, b ={5,9,7}, c 1=-2 a + b, c 2=3 a -2 b.
2.6. a ={1,4,-2}, b ={1,1,-1}, c 1= a + b, c 2=4 a +2 b.
2.7. a ={1,-2,5}, b ={3,-1,0}, c 1=4 a -2 b, c 2= b -2 a.
2.8. a ={3,4,-1}, b ={2,-1,1}, c 1=6 a -3 b, c 2= b -2 a.
2.9. a ={-2,-3,-2} b ={1,0,5}, c 1=3 a +9 b, c 2=3 b -6 a.
2.10. a ={-1,4,2}, b ={3,-2,6}, c 1=2 a - b, c 2=3 b -6 a.
2.11. a ={5,0,-1}, b ={7,2,3}, c 1=2 a - b, c 2=3 b -6 a.
2.12. a ={0,3,-2}, b ={1,-2,1}, c 1=5 a -2 b, c 2=3 a +5 b.
2.13. a ={-2,7,-1}, b ={-3,5,2}, c 1=2 a +3 b, c 2=3 a +2 b.
2.14. a ={3,7,0}, b ={1,-3,4}, c 1=4 a -2 b, c 2= b -2 a.
2.15. a ={-1,2,-1}, b ={2,-7,1}, c 1=6 a -2 b, c 2= b -3 a.
2.16. a ={7,9,-2}, b ={5,4,3}, c 1=4 a - b, c 2=4 b - a.
2.17. a ={5,0,-2}, b ={6,4,3}, c 1=5 a -3 b, c 2=6 b -10 a.
2.18. a ={8,3,-1}, b ={4,1,3}, c 1=2 a - b, c 2=2 b -4 a.
2.19. a ={3,-1 6}, b ={5,7,10}, c 1=4 a -2 b, c 2= b -2 a.
2.20. a ={1,-2,4}, b ={7,3,5}, c 1=6 a -3 b, c 2= b -2 a.
2.21. a ={3,7,0}, b ={4,6,-1}, c 1=3 a +2 b, c 2=5 a -7 b.
2.22. a {2,-1,4}, b ={3,-7,-6}, c 1=2 a -3 b, c 2=3 a -2 b.
2.23. a ={5,-1,-2}, b ={6,0,7}, c 1=3 a -2 b, c 2=4 b -6 a.
2.24. a ={-9,5,3}, b ={7,1,-2}, c 1=2 a - b, c 2=3 a +5 b.
2.25. a ={4,2,9}, b ={0,-1,3}, c 1=4 b -3 a, c 2=4 a -3 b.
2.26. a ={2,-1,6}, b ={-1,3,8}, c 1=5 a -2 b, c 2=2 a -5 b.
2.27. a ={5,0,8}, b ={-3,1,7}, c 1=3 a -4 b, c 2=12 b -9 a.
2.28. a ={-1,3,4}, b ={2,-1,0}, c 1=6 a -2 b, c 2= b -3 a.
2.29. a {4,2,-7}, b ={5,0,-3}, c 1= a -3 b, c 2=6 b -2 a.
2.30. a ={2,0,-5}, b ={1,-3,4}, c 1=2 a -5 b, c 2=5 a -2 b.
Задание 3. Даны точки А, В, С. Найти косинус угла между векторами 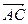 и
и 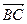 .
.
|
3.2. А (0,-3,6), В (-12,-3,-3), С (-9,-3,-6).
3.3. А (3,3,-1), В (5,5,-2), С (4,1,1).
3.4. А (-1,2,-3), В (3,4,-6), С (1,1,-1).
3.5. А (-4,-2,0), В (-1,-2,4), С (3,-2,1).
3.6. А (5,3,-1), В (5,2,0), С (6,4,-1).
3.7. А (-3,-7,-5), В (0,-1,-2), С (2,3,0).
3.8. А (2,-4,6), В (0,-2,4 С (6,-8,10).
3.9. А (0,1,-2), В (3,1,2), С (4,1,1).
3.10. А (3,3,-1), В (1,5,-2), С (4,1,1).
3.11.. А (2,1,-1), В (6,-1,-4), С (4,2,1).
3.12. А (-1,-2,1), В (-4,-2,5), С (-8,-2,2).
3.13. А (6,2,-3), В (6,3,-2), С (7,3,-3).
3.14. А (0,0,4), В (-3,-6,1), С (-5,-10,-1).
3.15. А (2,-8,-1), В (4,-6,0), С (-2,-5,-1).
3.16. А (3,-6,9), В (0,-3,6), С (9,-12,15).
3.17. А (0,2,-4), В (8,2,2), С (6,2,4).
3.18. А (3,3,-1), В (5,1,-2), С (4,1,1).
3.19. А (-4,3,0), В (0,1,3), С (-2,4,-2).
3.20. А (1,-1,0), В (-2,-1,4), С (8,-1,-1).
3.21. А (7,0,2), В (7,1,3), С (8,-1,2).
3.22. А (2,3,2), В (-1,-3,-1), С (-3,-7,-3).
3.23. А (2,2,7), В (0,0,6), С (-2,5,7).
3.24. А (-1,2,-3), В (0,1,-2), С (-3,4,-5).
3.25. А (0,3,-6), В (9,3,6), С (12,3,3).
3.26. А (3,3,-1), В (5,1,-2), С (4,1,-3).
3.27. А (-2,1,1), В (2,3,-2), С (0,0,3).
3.28. А (1,4,-1), В (-2,4,-5), С (8,4,0).
3.29. А (0,1,0), В (0,2,1), С (1,2,0).
3.30. А (-4,0,4), В (0,2,-4), С (-6,8,-10).
Задание 4. Вычислить площадь параллелограмма, построенного на векторах a и b.
4.1. a = p +2 q; b =3 p - q; | p |=1; | q |=2; (p ^ q)=  ;
;
4.2. a =3 p + q; b = p -2 q; | p |=4; | q |=1; (p ^ q)=  ;
;
4.3. a = p -3 q; b = p +2 q; | p |=1/5; | q |=1; (p ^ q)=  ;
;
4.4. a =3 p -2 q; b = p +5 q; | p |=4; | q |=1/2; (p ^ q)=  ;
;
4.5. a = p -2 q; b =2 p + q; | p |=2; | q |=3; (p ^ q)= 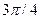 ;
;
4.6. a = p +3 q; b = p -2 q; | p |=2; | q |=3; (p ^ q)=  ;
;
4.7. a =2 p - q; b = p +3 q; | p |=3; | q |=2; (p ^ q)=  ;
;
4.8. a =4 p + q; b = p - q; | p |=7; | q |=2; (p ^ q)=  ;
;
4.9. a = p -4 q; b =3 p + q; | p |=1; | q |=2; (p ^ q)=  ;
;
4.10. a = p +4 q; b =2 p - q; | p |=7; | q |=2; (p ^ q)=  ;
;
4.11. a =3 p +2 q; b = p - q; | p |=10; | q |=1; (p ^ q)=  ;
;
4.12. a =4 p - q; b = p +2 q; | p |=5; | q |=4; (p ^ q)=  ;
;
4.13. a =2 p +3 q; b = p -2 q; | p |=6; | q |=7; (p ^ q)=  ;
;
4.14. a =3 p - q; b = p +2 q; | p |=3; | q |=4; (p ^ q)=  ;
;
4.15. a =2 p +3 q; b = p -2 q; | p |=2; | q |=3; (p ^ q)= 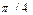 ;
;
4.16. a =2 p -3 q; b =3 p + q; | p |=4; | q |=1; (p ^ q)=  ;
;
4.17. a =5 p + q; b = p -3 q; | p |=1; | q |=2; (p ^ q)=  ;
;
4.18. a =7 p -2 q; b = p +3 q; | p |=1/2; | q |=2; (p ^ q)=  ;
;
4.19. a =6 p - q; b = p + q; | p |=3; | q |=4; (p ^ q)=  ;
;
4.20. a =10 p + q; b =3 p -2 q; | p |=4; | q |=1; (p ^ q)=  ;
;
4.21. a =6 p - q; b = p +2 q; | p |=8; | q |=1/2; (p ^ q)=  ;
;
4.22. a =3 p +4 q; b = q - p; | p |=2,5 | q |=2; (p ^ q)=  ;
;
4.23. a =7 p + q; b = p -3 q; | p |=3; | q |=1; (p ^ q)= 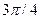 ;
;
4.24. a = p +3 q; b =3 p - q; | p |=3; | q |=5; (p ^ q)=  ;
;
4.25. a =3 p + q; b = p -3 q; | p |=7; | q |=2; (p ^ q)=  ;
;
4.26. a =5 p - q; b = p + q; | p |=5; | q |=3; (p ^ q)=  ;
;
4.27. a =3 p -4 q; b = p +3 q; | p |=2; | q |=3; (p ^ q)=  ;
;
4.28. a =6 p - q; b =5 q + p; | p |=1/2 | q |=4; (p ^ q)=  ;
;
4.29. a =2 p +3 q; b = p -2 q; | p |=2; | q |=1; (p ^ q)=  ;
;
4.30. a =2 p -3 q; b =5 p + q; | p |=2; | q |=3; (p ^ q)=  ;
;
Задание 5. Компланарны ли векторы a, b и c.
5.1. a ={2,3,1}; b ={-1,0,-1}; c ={2,2,2}.
5.2. a ={3,2,1}; b ={2,3,4}; c ={3,1,-1}.
5.3. a ={1,5,2}; b ={-1,1,-1}; c ={1,1,1}.
5.4. a ={1,-1,-3}; b ={3,2,1}; c ={2,3,4}.
5.5. a ={3,3,1}; b ={1,-2,1}; c ={1,1,1}.
5.6. a ={3,1,-1}; b ={-2,-1,0}; c ={5,2,-1}.
5.7. a ={4,3,1}; b ={1,-2,1}; c ={2,2,2}.
5.8. a ={4,3,1}; b ={6,7,4}; c ={2,0,-1}.
5.9. a ={3,2,1}; b ={1,-3,-7}; c ={1,2,3}.
5.10. a ={3,7,2}; b ={-2,0,-1}; c ={2,2,1}.
5.11. a ={1,-2,6}; b ={1,0,1}; c ={2,-6,17}.
5.12. a ={6,3,4}; b ={-1,-2,-1}; c ={2,1,2}.
5.13. a ={7,3,4}; b ={-1,-2,-1}; c ={4,2,4}.
5.14. a ={2,3,2}; b ={4,7,5}; c ={2,0,-1}.
5.15. a ={5,3,4}; b ={-1,0,-1}; c ={4,2,4}.
5.16. a ={3,10,5}; b ={-2,-2,-3}; c ={2,4,3}.
5.17. a ={-2,-4,-3}; b ={4,3,1}; c ={6,7,4}.
5.18. a ={3,1,-1}; b ={1,0,-1}; c ={8,3,-2}.
5.19. a ={4,2,2}; b ={-3,-3,-3}; c ={2,1,2}.
5.20. a ={4,1,2}; b ={9,2,5}; c ={1,1,-1}.
5.21. a ={5,3,4}; b ={4,3,3}; c ={9,5,8}.
5.22. a ={3,4,2}; b ={1,1,0}; c ={8,11,6}.
5.23. a ={4,-1,-6}; b ={1,-3,-7}; c ={2,-1,-4}.
5.24. a ={3,1,0}; b ={-5,-4,-5}; c ={4,2,4}.
5.25. a ={3,0,3}; b ={8,1,6}; c ={1,1,-1}.
5.26. a ={1,-1,4}; b ={1,0,3}; c ={1,-3,-8}.
5.27. a ={6,3,4}; b ={-1,-2,-1}; c ={2,1,2}.
5.28. a ={4,1,1}; b ={-9,-4,-9}; c ={6,2,6}.
5.29. a ={-3,3,3}; b ={-4,7,6}; c ={3,0,-1}.
5.30. a ={-7,-10,-5}; b ={0,-2,-1}; c ={-2,4,-1}.
Задание 6. Вычислить объем тетраэдра с вершинами в точках А 1, А 2, А 3 и А 4 и его высоту, опущенную из вершины А 4 на грань А 1 А 2 А 3.
6.1. A 1(1,3,6), A 2(2,2,1), A 3(-1,0,1), A 4(-4,6,-3).
6.2. A 1(-4,2,6), A 2(2,-3,0), A 3(-10,5,8), A 4(-5,2,-4).
6.3. A 1(7,2,4), A 2(7,-1,-2), A 3(3,3,1), A 4(-4,2,1).
6.4. A 1(2,1,4), A 2(-1,5,-2), A 3(-7,-3,2), A 4(-6,-3,6).
6.5. A 1(-1,-5,2), A 2(-6,0,-3), A 3(3,6,-3), A 4(-10,6,7).
6.6. A 1(0,-1,-1), A 2(-2,3,5), A 3(1,-5,-9), A 4(-1,-6,3).
6.7. A 1(5,2,0), A 2(2,5,0), A 3(1,2,4), A 4(-1,1,1).
6.8. A 1(2,-1,-2), A 2(1,2,1), A 3(5,0,-6), A 4(-10,9,-7).
6.9. A 1(-2,0,-4), A 2(-1,7,1), A 3(4,-8,-4), A 4(1,-4,6).
6.10. A 1(14,4,5), A 2(-5,-3,2), A 3(-2,-6,-3), A 4(-2,2,-1).
6.11. A 1(1,2,0), A 2(3,0,-3), A 3(5,2,6), A 4(8,4,-9).
6.12. A 1(2,-1,2), A 2(1,2,-1), A 3(3,2,1), A 4(-4,2,5).
6.13. A 1(1,1,2), A 2(-1,1,3), A 3(2,-2,4), A 4(-1,0,-2).
6.14. A 1(2,3,1), A 2(4,1,-2), A 3(6,3,7), A 4(7,5,-3).
6.15. A 1(1,1,-1), A 2(2,3,1), A 3(3,2,1), A 4(5,9,-8).
6.16. A 1(1,5,-7), A 2(-3,6,3), A 3(-2,7,3), A 4(-4,8,-12).
6.17. A 1(-3,4,-7), A 2(1,5,-4), A 3(-5,-2,0), A 4(2,5,4).
6.18. A 1(-1,2,-3), A 2(4,-1,0), A 3(2,1,-2), A 4(3,4,5).
6.19. A 1(4,-1,3), A 2(-2,1,0), A 3(0,-5,1), A 4(3,2,-6).
6.20. A 1(1,-1,1), A 2(-2,0,3), A 3(2,1,-1), A 4(2,-2,-4).
6.21. A 1(1,2,0), A 2(1,-1,2), A 3(0,1,-1), A 4(-3,0,1).
6.22. A 1(1,0,2), A 2(1,2,-1), A 3(2,-2,1), A 4(2,1,0).
6.23. A 1(1,2,-3), A 2(1,0,1), A 3(-2,-1,6), A 4(0,-5,-4).
6.24. A 1(3,10,-1), A 2(-2,3,-5), A 3(-6,0,-3), A 4(1,-1,2).
6.25. A 1(-1,2,4), A 2(-1,-2,-4), A 3(3,0,-1), A 4(7,-3,1).
6.26. A 1(0,-3,1), A 2(-4,1,2), A 3(2,-1,5), A 4(3,1,-4).
6.27. A 1(1,3,0), A 2(4,-1,2), A 3(3,0,1), A 4(-4,3,5).
6.28. A 1(-2,-1,-1), A 2(0,3,2), A 3(3,1,-4), A 4(-4,7,3).
6.29. A 1(-3,-5,6), A 2(2,1,-4), A 3(0,-3,-1), A 4(-5,2,-8).
6.30. A 1(1,-1,2), A 2(2,1,2), A 3(1,1,4), A 4(6,-3,8).
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Задание 1 Найти расстояние от точки М 0 до плоскости, проходящей через три точки М 1, М 2, М 3.
1.1. М 1(-3,4,-7), М 2(1,5,-4), М 3(-5,-2,0), М 0(-12,7,-1).
1.2. М 1(-1,2,-3), М 2(4,-1,0), М 3(2,1,-2), М 0(1,-6,-5).
1.3. М 1(-3,-1,1), М 2(-9,1,-2), М 3(3,-5,4), М 0(-7,0,-1).
1.4. М 1(1,-1,1), М 2(-2,0,3), М 3(2,1,-1), М 0(-2,4,2).
1.5. М 1(1,2,0), М 2(1,-1,2), М 3(0,1,-1), М 0(2,-1,4).
1.6. М 1(1,0,2), М 2(1,2,-1), М 3(2,-2,1), М 0(-5,-9,1).
1.7. М 1(1,2,-3), М 2(1,0,1), М 3(-2,-1,6), М 0(3,-2,-9).
1.8. М 1(3,10,-1), М 2(-2,3,-5), М 3(-6,0,-3), М 0(-6,7,-10).
1.9. М 1(-1,2,4), М 2(-1,-2,-4), М 3(3,0,-1), М 0(-2,3,5).
1.10. М 1(0,-3,1), М 2(-4,1,2), М 3(2,-1,5), М 0(-3,4,-5).
1.11. М 1(1,3,0), М 2(4,-1,2), М 3(3,0,1), М 0(4,3,0).
1.12, М 1(-2,-1,-1), М 2(0,3,2), М 3(3,1,-4), M 0(-21,20,-16).
1.13. М 1(-3,-5,6), М 2(2,1,-4), М 3(0,-3,-1), М 0(3,6,68).
1.14. М 1(2,-4,-3), М 2(5,-6,0), М 3(-1,3,-3), М 0(2,-10,8).
1.15. М1(1,-1,2), М 2(2,1,2), М 3(1,1,4), М 0(-3,2,7).
1.16. М 1(1,3,6), М 2(2,2,1), М 3(-1,0,1), М 0(5,-4,5).
1.17. М 1(-4,2,6), М 2(2,-3,0), М 3(-10,5,8), М 0(-12,1,8).
1.18. М 1(7,2,4), М 2(7,-1,-2), М 3(-5,-2,-1), М 0(10,1,8).
1.19. М 1(2,1,4), М 2(3,5,-2), М 3(-7,-3,2), М 0(-3,1,8).
1.20. М 1(-1,-5,2), М 2(-6,0,-3), М 3(3,6,-3), М 0(10,-8,-7).
1.21. М 1(0,-1,-1), М 2(-2,3,5), М 3(1,-5,-9), М 0(-4,-13,6).
1.22. М 1(5,2,0), М 2(2,5,0), М 3(1,2,4), М 0(-3,-6,-8).
1.23. М 1(2,-1,-2), М 2(1,2,1), М 3(5,0,-6), М 0(14,-3,7).
1.24. М 1(-2,0,-4), М 2(-1,7,1), М 3(4,-8,-4), М 0(-6,5,5).
1.25. М 1(14,4,5), М 2(-5,-3,2), М 3(-2,-6,-3), М 0(-1,-8,7).
1.26. М 1(1,0,2), М 2(3,0,-3), М 3(5,2,6), М 0(-13,-8,16).
1.27. М 1(2,-1,2), М 2(1,2,-1), М 3(3,2,1), М 0(-5,3,7).
1.28. М 1(1,1,2), М 2(-1,1,3), М 3(2,-2,4), М 0(2,3,8).
1.29. М 1(2,3,1), М 2(4,1,-2), М 3(6,3,7), М 0(-5,-4,7).
1.30. М 1(1,1,-1), М 2(2,3,1), М 3(3,2,1), М 0(-3,-7,6).
|
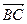 .
.
2.1. A (1,0,-2), B (2,-1,3), C (0,-3,2).
2.2. A (-1,3,4), B (-1,5,0), C (2,6,1).
2.3. A (4,-2,0), B (1,-1,-5), C (-2,1,-3).
2.4. A (-8,0,7), B (-3,2,4), C (-1,4,5).
2.5. A (7,-5,1), B (5,-1,-3), C (3,0,-4).
2.6. A (-3,5,-2), B (-4,0,3), C (-3,2,5).
2.7. A (1,-1,8), B (-4,-3,10), C (-1,-1,7).
2.8. A (-2,0,-5), B (2,7,-3), C (1,10,-1).
2.9. A (1,9,-4), B (5,7,1), C (3,5,0).
2.10. A (-7,0,3), B (1,-5,-4), C (2,-3,0).
2.11. A (0,-3,5), B (-7,2,6), C (-3,2,4).
2.12. A (5,-1,2), B (2,-4,3), C (4,-1,3).
2.13. A (-3,7,2), B (3,5,1), C (4,5,3).
2.14. A (0,-2,8), B (4,3,2), C (1,4,3).
2.15. A (1,-1,5), B (0,7,8), C (-1,3,8).
2.16. A (-10,0,9), B (12,4,11), C (8,5,15).
2.17. A (3,-3,-6), B (1,9,-5), C (6,6,-4).
2.18. A (2,1,7), B (9,0,2), C (9,2,3).
2.19. A (-7,1,-4), B (8,11,-3), C (9,9,-1).
2.20. A (1,0,-6), B (-7,2,1), C (-9,6,1).
2.21. A (-3,1,0), B (6,3,3), C (9,4,-2).
2.22. A (-4,-2,5), B (3,-3,-7), C (9,3,-7).
2.23. A (0,-8,10), B (-5,5,7), C (-8,0,4).
2.24. A (1,-5,-2), B (6,-2,1), C (2,-2,-2).
2.25. A (0,7,-9), B (-1,8,-11), C (-4,3,-12).
2.26. A (-3,-1,7), B (0,2,-6), C (2,3,-5).
2.27. A (5,3,-1), B (0,0,-3), C (5,-1,0).
2.28. A (-1,2,-2), B (13,14,1), C (14,15,2).
2.29. A (7,-5,0), B (8,3,-1), C (8,5,1).
2.30. A (-3,6,4), B (8,-3,5), C (10,-3,7).
Задание 3. Найти угол между плоскостями.
3.1. 
3.2. 
3.3. 
3.4. 
3.5. 
3.6. 
3.7. 
3.8. 
3.9. 
3.10. 
3.11. 
3.12. 
3.13 
3.14. 
3.15. 
3.16. 
3.17. 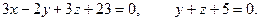
3.18 
3.19. 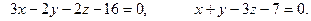
3.20. 
3.21. 
3.22. 
3.23 
3.24. 
3.25. 
3.26. 
3.27. 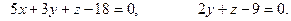
3.28. 
3.29. 
3.30. 
Задание 4. Найти координаты точки А, равноудаленной от точек В и С.
4.1. А (0, 0, z), В (5, 1, 0), С (0, 2, 3).
4.2. А (0, 0, z), В (3, 3, 1), С (4, 1, 2).
4.3. А (0, 0, z), В (3, 1, 3), С (1, 4, 2).
4.4. А (0, 0, z), В (-1, -1, -6), С (2, 3, 5).
4.5. А (0, 0, z), В (-13, 4, 6), С (10,-9, 5).
4.6. А (0, 0, z), В (-18, 1, 0), С (15, -10, 2).
4.7. А (0, 0, z), В (10, 0, -2), С (9, -2, 1).
4.8. А (0, 0, z), В (-5, -5, 6), С (-7, 6, 2).
4.9. А (0, 0, z), В (-6, 7, 5), С (8, -4, 3).
4.10. А (0, 0, z), В (6, -7, 1), С (-1, 2, 5).
4.11. А (0, 0, z), В (7, 0 -15), С (2, 10 -12).
4.12. А (0, y, 0), В (3, 0, 3), С (5, 7, 1).
4.13. А (0, y, 0), В (1, 6, 4), С (5, 7, 1).
4.14. А (0, y, 0), В (-2, 8, 10), С (6, 11, -2).
4.15. А (0, y, 0), В (-2, -4, 6), С (7, 2, 5).
4.16. А (0, y, 0), В (2, 2, 4), С (0, 4, 2).
4.17. А (0, y, 0), В (0, -4, 1), С (1, -3, 5).
4.18. А (0, y, 0), В (0, 5, -9), С (-1, 0, 5).
4.19. А (0, y, 0), В (-2, 4, -6), С (8, 5, 1).
4.20. А (0, y, 0), В (7, 3, -4), С (1, 5, 7).
4.21. А (0, y, 0), В (0, -2, 4), С -4, 0, 4).
4.22. А (x, 0, 0), В (0, 1, 3), С (2, 0, 4).
4.23. А (x, 0, 0), В (8, 1, -7), С (10, -2, 1).
4.24. А (x, 0, 0), В (4, 0, 5), С (5, 4, 2).
4.25. А (x, 0, 0), В (3, 5, 6), С (1, 2, 3.
4.26. А (x, 0, 0), В (4, 5, -2), С (2, 3, 4).
4.27. А (x, 0, 0), В (-2, 0, 6), С (0, -2, -4).
4.28. А (x, 0, 0), В (1, 5, 9), С (3, 7, 11).
4.29. А (x, 0, 0), В (4, 6, 8), С (2, 4, 6).
4.30. А (x, 0, 0), В (1, 2, 3), С (2, 6, 10).
Задание 5. Написать канонические уравнения прямой.
5.1. 
5.2. 
5.3. 
5.4. 
5.5. 
5.6.  .
.
5.7. 
5.8. 
5.9.  .
.
5.10.  .
.
5.11. 
 5.12.
5.12. 
5.13. 
5.14. 
5.15. 
5.16.  .
.
5.17. 
5.18. 
5.19. 
5.20.  .
.
5.21 
5.22. 
5.23. 
5.24. 
5.24.  .
.
5.25.  .
.
5.26. 
5.27. 
5.28. 
5.29. 
5.30. 
Задание 6. Найти точку пересечения прямой и плоскости
6.1.  .
.
6.2. 
6.3. 
6.4. 
6.5 
6.6.  .
.
6.7. 
6.8. 
6.9. 
6.10. 
6.11. 
6.12. 
6.13. 
6.14. 
6.15.  .
.
6.16. 
6.17.  .
.
6.18.  .
.
6.19. 
6.20. 
6.21. 
6.22. 
6.23. 
6.24 
6.25.  .
.
6.26.  .
.
6.27.  .
.
6.28.  .
.
6. 29.  .
.
6.30.  .
. 
Задание 7. Найти точку М 1, симметричную точке М относительно прямой (для вариантов 1-15) или плоскости (для вариантов 16-31).
7.1. 
7.2. 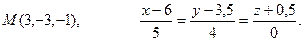
7.3. 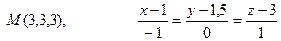
7.5. 
7.6. 
7.7






