С точки зрения молекулярно – кинетической теории внутренняя энергия вещества определяется суммой кинетических энергий всех молекул вещества и потенциальной энергией их взаимодействия. В случае идеального газа потенциальная энергия взаимодействия молекул равна нулю, соответственно внутренняя энергия будет определяться кинетической энергией всех молекул газа. При учёте только поступательного движения молекул средняя кинетическая энергия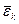 
молекулы определяется основным уравнением молекулярно – кинетической теории (3.11)
.
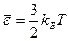Но кроме поступательного движения молекул газа, совершает и другие виды движений (вращательные, колебательные). Для расчета средней кинетической энергии молекул, с учётом различных видов движений воспользуемся классической теорией о равномерном распределении энергии по степеням свободы. Эту теорему можно сформулировать так: Если система молекул находиться в тепловом равновесии при температуре T, средняя кинетическая энергия молекулы равномерно распределена между всеми степенями свободы, причём для каждой степени свободы молекулы она равна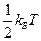 
.
Число степеней свободы – это число независимых координат, определяющих положение тела в пространстве. Если вещество состоит из атомов, атомы можно представить как материальную точку, положение которой можно определить, задав три координаты X,Y,Z центра атома. Если обозначим через n число атомов в молекуле, и через i число степеней свободы, то при n=1 i=3. Если рассмотреть простейший случай двухатомной молекулы её можно представить в виде системы состоящей из двух атомов, расположенных на некотором расстоянии друг от друга (рис.1).
|
Если же молекула состоит из 3-х и более атомов, то она имеет 3 степени свободы, связанных с поступательным движением центра масс и 3 степени свободы с вращательным движение вокруг осей X,Y,Z (рис.2), т.е. при n³3 i=6.
Но атомы в молекулах не всегда жёстко связано друг с другом и могут совершать колебания друг относительно друга. Тогда требуется ещё одна координата для определения конфигурации молекулы – это расстояние между атомами. В общем случае двухатомные молекулы обладают 6 степенями свободы: тремя поступательными, двумя вращательными и одной колебательной. Если молекула состоит из n атомов не жёстко связанных, то она имеет 3n степеней свободы (каждый атом имеет 3 степени свободы). Из этого числа 3 степени свободы поступательные, 3 степени свободы вращательные (за исключением случая когда атомы расположены по одной прямой), 3n-6 колебательные.
В случае, когда амплитуда колебаний меньше, чем расстояние между атомами, то такие колебания называют гармоническими, атомы в этом случае являются гармоническими осцилляторами. Но осциллятор обладает не только кинетической, но и потенциальной энергией. Для гармонического осциллятора, как известно из механики, среднее значение кинетической и потенциальной энергии равны между собой. Поэтому на одну колебательную степень свободы будет приходиться энергия равная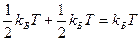 
. Обычно при расчете кинетической энергии молекул предполагают, что на все степени свободы приходиться одна и та же энергия 
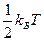, но число колебательных степеней свободы удваиваются. Если число степеней свободы молекулы i, то её средняя кинетическая энергия равна
.
Пусть данный идеальный газ содержит N молекул, которые имеют i степени свободы. Внутренняя энергия такого газа будет равна
.
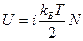Если же имеем один моль идеального газа, то N=NA, соответственно
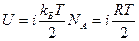. (3.26)
Из формулы (3.26) следует, что внутренняя энергия идеального газа зависит только от температуры. Это является теоретическим подтверждением закона Джоуля, который был установлен опытным путем.
