Из анализа цикла Карно следует, что нельзя полностью превратить в механическую работу тепловую энергию, полученную от нагревателя. Часть этого тепла непременно должна быть передана холодильнику. Если количество теплоты, полученное рабочим телом от нагревателя, равно Q0, а в работу преобразована часть Q0-Q1 этой теплоты, то соотношение
представляет коэффициент полезного действия кругового процесса. Как следует из формулы (1.35), коэффициент полезного действия (КПД) цикла Карно определяется равенством
.
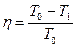Полученное значение КПД является наибольшим, потому что полностью все процессы цикла Карно были обратимыми. В природе нет замкнутых циклов с КПД больше чем у цикла Карно.
Приведем теоремы Карно: 1) Тепловая машина, работающая при данных значениях температур нагревателя и холодильника, не может иметь КПД, больше чем машина, работающая по обратимому циклу Карно при тех же значениях температур нагревателя и холодильника. 2) КПД цикла Карно не зависит от рабочего тела, а зависит только от температур нагревателя и холодильника.
Холодильная машина
Обратимый процесс характеризуется тем, что если его провести в обратном направлении, то тело, участвующее в процессе пройдёт через те же состояния, но в обратном порядке.
Если цикл Карно провести в обратном направлении, то тепло будет передаваться не от нагревателя к холодильнику, наоборот, от холодильника к нагревателю (рис.4). Если процесс идёт, как показано стрелкой, полезная работа буде меньше, чем работа, совершаемая внешними силами. Поэтому результатом обратного цикла Карно будет не внешняя полезная работа, а перенос тепла от холодильника к нагревателю, т. е. перевод от менее нагретого тела к более нагретому телу. Если прямой цикл Карно служит для превращение теплоты в работу, то машина действующая по обратному циклу Карно используется для передачи тепла от менее нагретого тела к более нагретому, т. е. является холодильной машиной. С её помощью за счёт внешней работы тепло отнимается у более холодного тела и передаётся к более нагретому.
Поскольку КПД цикла Карно является максимальным, имеем следующее неравенство
(1.36)
где Q0 -количество теплоты, отданное рабочему телу нагревателем, а Q1 -количество теплоты полученное от рабочего тела холодильником.
Но если рассматривать процесс с точки зрения изменений, происходящих в самом рабочем теле, то Q0 и Q1 – это количество теплоты полученное и отданное рабочим телом. Этим величинам Q0 и Q1 нужно, очевидно, приписать противоположные знаки.
Будем считать полученное телом количество теплоты Q0 положительным, тогда Q1 - отрицательно. Следовательно, неравенство (1.36) перепишется в виде
или
(1.37)
Если круговой процесс является обратимым, то
(1.38)
Таким образом, в случае цикла Карно, сумма отношений теплот участков к их температурам, для всего замкнутого контура равна нулю.
Свободная энергия
Представим, что система совершает изотермический процесс (расширение или сжатие). Расширяясь, газ, может произвести механическую работу, следовательно, газ обладает некоторой энергией. Та часть энергии, которая при данном условии может быть превращена в механическую работу, называется свободной энергией.
Система не может совершить работу, превышающую значение её свободной энергии. В механике механическая макроскопическая энергия системы может быть полностью превращена в работу. Внутренняя энергия молекулярной системы в случае изотермического процесса не может быть целиком превращена в работу. Поэтому, если мы интересуемся величиной работы, которую система в данном состоянии может произвести при изотермическом процессе, то внутренняя энергия не является подходящей характеристикой этого состояния. Внутренняя энергия характеризует состояние системы, если интересуемся работой, которую способна эта система произвести при адиабатическом процессе A=DU. Свободная энергия должна характеризовать систему с точки зрения её работоспособности при изотермическом изменении её состояния.
Свободная энергия системы измеряется работой, которую может произвести система, изменяя своё состояние изотермически и обратимо от состояния, в котором она находится, до выбранного нами начального состояния, при котором свободная энергия предполагается равной нулю, dA=-dF, где F - свободная энергия.
Внутренняя энергия идеального газа не зависит от занимаемого им объёма: один моль газа сжатый в баллоне имеет такую же внутреннюю энергию как и не сжатый газ при той же температуре. Но сжатый газ имеет большую свободную энергию, поскольку при изотермическом расширении может совершать большую работу. В случае необратимых процессов dA<dF.
Возможны такие случаи, когда изменение свободной энергии вообще не сопровождается совершением работы. Если идеальный газ расширится в пустоту, то никакой работы не совершается. Температура, а значит, и внутренняя энергия газа также остаются неизменными. Между тем свободная энергия газа уменьшается, так как уменьшается работа, которую газ может совершить.
Энтропия
Из цикла Карно мы видим, что количество тепла, которое должно быть доставлено телу или отнято у него при переходе из одного состояние в другое не определяется начальными и конечными состояниями, но существенно зависит от способа осуществления этого перехода. Функция Q не является функцией состояния, как внутренняя энергия и свободная энергия. Это видно из уравнения первого закона термодинамики
dQ=dU+dA.
Так как dA зависит от пути перехода, то и dQ будет зависеть от способа перехода из одного состояния в другое. Количество теплоты Q0, доставленное телу от нагревателя при температуре T0 не равно количеству теплоты Q1, переданное им холодильнику при температуре T1 . В то же время равны между собой
.
Величину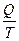 
называют приведённой теплотой и это равенство говорит о равенстве приведённых тепло, полученных или отданных рабочим телом при круговом процессе. Кроме того, как следует из выражения (1.38), сумма приведенных теплот в замкнутом цикле Карно равняется нулю. Эта особенность теплоты позволяет ввести особую термодинамическую величину- энтропию, имеющую фундаментальное значение в физике.
Любое изменение состояния тела в общем случае можно представить как результат бесконечно большого числа бесконечно малых изменений. При таком бесконечно малом изменении состояния система либо поглощает, либо выделяет бесконечно малое количество тепла dQ. Можно показать, что если в результате каких-либо изменений состояния обратимым путём система переходит из состояния A в состояние B, то сумма приведённых количеств теплоты
не зависит от пути от A к B, для круговых процессов 
. Это даёт нам право утверждать, что присутствует некоторая величина S, являющаяся функцией состояния системы, причем
.
Эта формула позволяет определить не абсолютное значение функции, соответствующее данному состоянию, а лишь её изменением при переходе от одного состояния к другому. Обычно значение энтропии одного из состояний берут равной нулю. Тогда
.
Это и есть энтропия системы в данном состоянии. На практике важно только изменение энтропии при изменении состояния системы, поэтому неважно, к какому состоянию приписать нулевое значение энтропии. Принято считать энтропию равной нуль в состоянии, когда T=0.
Таким образом, элементарное изменение энтропии определяется выражением
.
Отметим, что dQ не является полным дифференциалом, так как Q не является функцией состояния, dQ становится полным дифференциалом после деления на T. Величина 1/T является интегрирующим множителем для dQ.
С учетом выражения для dS первый закон термодинамики можно записать в виде
. (1.39)
Это уравнение носит название термодинамического тождества. Его называют вторым началом термодинамики для обратимых процессов. Если круговой процесс, претерпеваемый системой необратим, то
.
Это выражение называется неравенством Клаузиуса.
