Энтропия, будучи функцией состояния тела, может служить таким же параметром состояния тела как T,V,P. Энтропия S может быть выражена через любые из двух параметров P,V,T. Рассмотрим, как это делается. Это тем более интересно, поскольку S нельзя измерить на эксперименте.
Из термодинамического тождества (1.39) имеем
,
.
Из любых из четырёх величин T,S,P и V, входящих в это уравнение, можно выбрать в качестве независимых переменных две, через которые можно выразить остальные. Выберем в качестве независимых переменных T и Р, то есть состояние системы изменяется в результате изменения T и Р. Вычислим изменение dS. Поскольку энтропия является функцией состояния, ее полный дифференциал dS можно представить в виде
. (1.40)
Учитывая, что, 
где СР –теплоемкость при постоянном давлении, выражение (1.40) имеет вид
. (1.41)
Для расчета производной 
воспользуемся методом термодинамических потенциалов. Одним из потенциалов термодинамики является внутренняя энергия U, дифференциал которой равен
dU=TdS-PdV (1.42)
Введем еще потенциалы:
H= U+PV - энтальпия или теплосодержание;
F=U-TS - cвободная энергия;
Ф=U-TS+PV - большой термодинамический потенциал.
Дифференциалы этих потенциалов с учетом (1.42) имеют вид:
dH=TdS+VdP
dF=-SdT-PdV
dФ=-SdT+VdP.
Поскольку все термодинамические потенциалы являются функциями состояния и имеют полные дифференциалы, для них справедливы соотношения
, (1.43)
, (1.44)
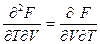, (1.45)
. (1.46)
Из (1.43) с учетом выражения (1.42) для dU имеем
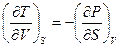. (1.47)
Из (1.44) с учетом выражения для dH получим
. (1.48)
Из (1.45) с учетом выражения для dF получим
. (1.49)
Из (1.46) и выражения для dФ имеем
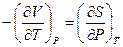. (1.50)
Выражения (1.47)-(1.50) называют соотношениями Максвелла.
Формулу (1.41), используя соотношение (1.47), перепишем в виде
. (1.51)
Считая, что энтропия является функцией температуры и объема, используя соотношение (1.49), можно записать следующее выражение для дифференциала энтропии
.
Поскольку
(1.52)
Используя (1.51) и (1.52) можно вычислить энтропию для данной массы вещества при данных значениях объема V и температуры Т, которую обозначим S(T,V), или при данных значениях давления Р и температуры Т S(P,T), если известны значения энтропии S(T0,V0) и S(T0,P0) при каких-нибудь других значениях этих параметров V0 и Т0 или Р0 и Т0..
Пусть система переходит из состояния 1 в состояние 2 по пути, указанной на рис. 4а. Поскольку энтропия является функцией состояния и ее изменение не зависит от формы пути, а определяется конечным и начальным состоянием,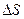 
по пути 12 совпадет со значением изменения энтропии 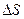по пути 1а2, т.е.
.
.
В частности для 1 моля идеального газа
,
а
так как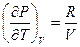 
.
Таким образом, для идеального газа
.
Это значит, что энтропия идеального газа возрастает с увеличением объема и температуры.
