Процесс, происходящий без подвода и отвода тепла, называется адиабатическим. Применим I закон термодинамики для определения связи между параметрами, определяющими состояние идеального газа, когда газ совершает адиабатический процесс.
Полагая в (1.13) dQ=0, dU=CvdT, получим
CvdT=-PdV (1.23)
Как следует из формулы (1.23) при адиабатическом расширении dV>0, dT<0, что значит температура тела понижается. Наоборот, при сжатии dV<0, dT>0 температура тела повышается. Это связано с тем, что адиабатически расширяющийся газ совершает работу за счёт собственной внутренней энергии, поэтому его температура понижается. Для получения уравнения адиабатического процесса, в переменных давление P и объём V, необходимо в уравнении (1.23) исключить температуру T. Это можно сделать, воспользовавшись уравнением состояния
,
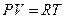дифференцирование которого даёт
PdV+ VdP=RdT
Откуда
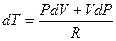(1.24)
Подставляя это значение dT в (1.23) получим
.
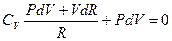После замены R равным ему значением Cp-Cv=R и приведения к общему знаменателю имеем
CVVdP+CpPdV=0.
Обозначим отношение теплоёмкостей
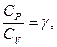
тогда последнее уравнение принимает вид
.
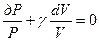Проинтегрируем это выражение в предположении, что g - постоянная величина:
.
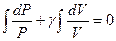После интегрирования получим
lnР+glnV=const,
или
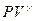=const, (1.25)
которое даёт искомое соотношение между давлением и объёмом идеального газа при адиабатическом процессе изменения объёма.
Уравнение (1.25) называется уравнением Пуассона или уравнением адиабаты,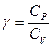 
- показатель адиабаты.
Из уравнения Пуассона видно, что в отличие от изотермического процесса, при адиабатическом процессе давление газа меняется обратно не первой степени объёма, а Vg, причём g больше единицы, так как Cp>Cv.
Так как g>1, то кривая P=f(V) при адиабатическом процессе, называемая адиабатой, круче изотермы. Более крутое падение давления с увеличением объёма при адиабатном процессе объясняется тем, что при адиабатном расширении идеального газа его давление уменьшается не только за счёт увеличения объёма, но и вследствие происходящего при этом понижения температуры газа.
Нетрудно найти связь другими термодинамическими параметрами газа при адиабатическом процессе. Если мы хотим найти связи между V и T при адиабатическом процессе, то необходимо в уравнении Пуассона (1.25) исключить P, воспользуясь уравнением состояния. Поставив в (1.25)
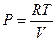
получаем
,
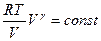или
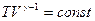. (1.26)
Здесь мы учли, что const/R также является постоянной величиной. Если в уравнение (1.25) вместо V поставим его значение
,
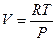то получим
.
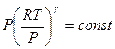После преобразования
.
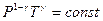Возвысив обе части последнего равенства в степень 1/g, получаем
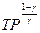=const (1.27)
Уравнение (1.27) представляет уравнение адиабатического процесса в переменных P и T.
