Математические действия с результатами измерений. Определение результата косвенных измерений

При косвенных измерениях значение искомой величины получают на основании известной зависимости, связывающей ее с другими величинами, значения которых получены путем измерения.

В общем случае

Y=f(X₁, X₂, …, X_n) (31)

В состав аргументов в правой части уравнения (31) входят не только величины, значения которых определяют в данном опыте путем измерения, но и величины, значения которых являются справочными данными или найдены в предыдущих опытах (так называемые заимствованные величины).

Учитывая случайный характер оценок значений величин, подставляемых в расчетную зависимость, для вычислений используем формулы теории вероятностей [5].

Для нахождения математического ожидания и границ рассеяния величины Y представим зависимость (31) приближенно в виде линейной функции (разложение в ряд Тейлора). Ограничимся производными не более второго порядка

Здесь (a ₁, a ₂, …, a_i,… a_n) – точка, в окрестностях которой осуществляется разложение функции.

Математическое ожидание оценки значения величины Y будет равно

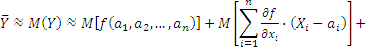
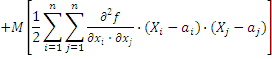
Или

В формулу (32) подставляют a ₁, a ₂, …, a_i,… a_n, равные оценкам значений величин X_i. (Оценка значения величины - это показание средства измерений при однократном измерении и среднее арифметическое значение совокупности отсчетов - при многократном измерении; для заимствованной величины – справочное значение.)

Разность M(X_i) – a_i равна (со знаком минус) отклонению оценки значения величины от математического ожидания, то есть - систематической погрешности. Если систематические погрешности исключены введением поправок, то имеем M(X_i) = a_i. Тогда запись формулы (32) упростится

Здесь и ниже для обозначения среднего квадратического отклонения использована буква σ традиционная для теории вероятностей.

Из сопоставления формул (32) и (33) вытекает обоснованность требования, чтобы перед выполнением математических операций значения поправок, обусловленные систематическими погрешностями, были внесены в результаты измерений.

Коэффициент корреляции ρ_ij характеризует взаимосвязь между изменениями величин, обусловленными влиянием одних и тех же факторов. Возможные значения коэффициента корреляции лежат в границах –1 < ρ_ij < +1. При положительной корреляции, когда при увеличении X_i, вызванном изменением какого-либо фактора, наблюдается увеличение X_j, ρ_ij >0. При отрицательной корреляции их изменения противоположны и ρ_ij <0. Оценки X_i и X_j независимы (ρ_ij =0), если изменение одной из них не сопровождается ожидаемым изменением другой.

Взаимная корреляция результатов измерений может быть обусловлена: взаимным пространственным расположением измерительных каналов; плохим экранированием; зависимостью погрешностей разных средств измерений, применяемых при данных косвенных измерениях, от одних и тех же влияющих величин и др.

Наличия корреляции можно ожидать в тех случаях, когда величины измеряют одновременно средствами измерений одного типа (одним и тем же средством измерений). В некоторых случаях причиной корреляции может быть оператор, выполняющий измерения.

При выполнении многократных косвенных измерений коэффициент корреляции вычисляют по формуле

Здесь буквой l обозначен порядковый номер совместного наблюдения оценок значений величин X_i и X_j; m – общее число наблюдений; 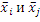- средние арифметические значения оценок, полученных при измерении величин X_i и X_j

По формуле (34) вычисляют коэффициент корреляции между случайными погрешностями (стандартными неопределенностями типа А), полученными в результате многократных измерений. Для неисключенных систематических погрешностей и неопределенностей, относимых к типу В, он оценивается на основе анализа свойств применяемых средств измерений и метода измерений.

Так как в большинстве случаев точное значение коэффициента корреляции найти невозможно, то оценки значений величин X_i и X_j условно разделяют [15] на сильно коррелированные 0,7<| ρ_ij | < 1,0 и слабо коррелированные при | ρ_ij |<0,7. В первом случае принимают ρ_ij =+1,0 или ρ_ij = -1,0, во втором - ρ_ij = 0.

Если степень корреляции неизвестна, полезно оценить её влияние на результат вычислений, приняв последовательно ρ_ij =0 и ρ_ij =1.

При отсутствии корреляции

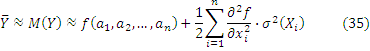
На практике, как правило, суммой дисперсий, которую называют поправкой на нелинейность, в формуле (35) пренебрегают ввиду её малости по сравнению со средним квадратическим отклонением (стандартной неопределенностью ) оценки математического ожидания величины Y. Расчет оценки значения величины Y ведут по формуле

Однако в некоторых ситуациях (например, при большом разбросе статистических данных) это может привести к заметной методической погрешности (см. примеры 39, 40 и 49 в книге [29]).

Определим дисперсию оценки значения величины Y. Согласно книге [5], в случае некоррелированных и независимых величин, справедлива формула

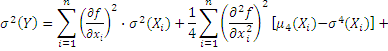
Формулу (36) можно применять в случаях, когда известны достоверные оценки центральных моментов μ₃ и μ₄.

Для величин, распределенных по закону, близкому к нормальному, запись формулы (36) существенно упрощается

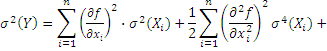
Руководство по выражению неопределенности измерений [24] предлагает следующие формулы для расчета суммарной дисперсии.

При незначительной нелинейности зависимости (31)

При значительной нелинейности, когда распределение каждого X_i располагается симметрично относительно среднего значения,

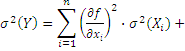
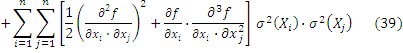
При незначительной нелинейности для коррелированных величин

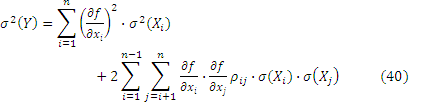
При вычислении значений частных производных во всех рассмотренных случаях подставляют оценки значений величин X_i, то есть a ₁, a ₂, …, a_i,… a_n.

Формулы (39) – (40) применяют для расчета как погрешности оценки величины Y, так и расширенной неопределенности. Запишем расчетные зависимости для некоррелированных случайных величин при незначительной нелинейности с учетом ранее принятых обозначений.