_______________
Комплексно – сопряженные числа -_______________________________________
____________
Задание 1.2.2 Сумма комплексных чисел а =2- i и в =-3-2 i равна __________.
Задание 1.2.3 Найти деление комплексных чисел а на в, если а =2+3 i и в =1+4 i.
Решение: ______________________________________________________________
_______________
Ответ:________________________________________________________________
Задание 1.2.4 Число вида 1+4 i является комплексно-сопряжённым для числа ________.
Задание 1.2.5 Разность комплексных чисел а =2+6 i и в =13-5 i равна __________.
Задание 1.2.6 Найти произведение комплексных чисел а =3-4 i и в =2+3 i.
Решение: ______________________________________________________________
_______________
Ответ:________________________________________________________________
Задание 1.2.7 Вычислить значение выражения (3-2 i)2.
а) 2+3 i;
б) 18+ i;
в) 3-4 i;
г) 11+11 i;
д) 5-12 i.
Задание 1.2.8 Значение выражения i 5 равно___________.
Задание 1.2.9 Решить уравнения 
; 
.
Решение: ______________________________________________________________
____________________________________________________________
Ответ:________________________________________________________________
Задание 1.2.10 Значение выражения i + i 2+ i 3+ i 4+ i 5 равно _______.
Функции и их графики
Функции и их графики
Задание 2.1.1 Дать определение функции.
Числовой функцией с областью определения 
называют _________________________________________________________________
Задание 2.1.2 Установить соответствия между графиками и функциями.
а) 
б) 
в) 
г) 
д) 
1 2 3 4 5 
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. |
Задание 2.1.3 Найти область определения функции 
a) R;
б) 
;
в) 
;
г) 
;
д) 
.
Задание 2.1.4 Область определения функции 
равна ______________.
Задание 2.1.5 Функция вида 
= 
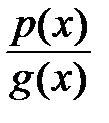, где 
– многочлены, называют ____________________________.
Задание 1.6 По рисунку определить графики функций изображенных фигур.
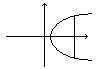
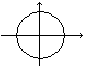
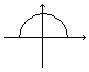
Задание 2.1.7 Найти область определения функции у = 
.
Решение:_____________________________________________________________ __________ Ответ: _______________________________________________________________
Задание 2. 1.8 Найти область определения и область значения функции 
.
Решение:_____________________________________________________________ __________ Ответ: _______________________________________________________________
Преобразование графиков
Задание 2.2.1 На графике указать графики функций 
; 
; 
.
Задание 2.2.2 Построить график функции 
с помощью элементарных преобразований.
Задание 2.2.3 По графику определить вид элементарного преобразования и формулу функции.
Решение:____________________________________________________________________________
Задание 2.2.4 Пошагово описать принцип построения графика функции 
1)________________________________________________________
2)________________________________________________________
3)________________________________________________________
Задание 2.2.5 В одной системе координат построить графики функций 
, 
, 
.
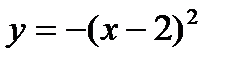Четные и нечетные функции
Задание 2.3.1 Дать определения.
Функция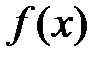 
называется ______, если для любого 
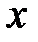из области определения выполняется равенство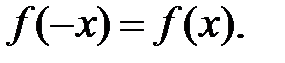 
Функция 
называется нечетной, если для любого 
из области определения выполняется равенство __________.
Задание 2.3.2 Указать четную функцию.
а) 
;
б) 
;
в) 
;
г) 
;
д) 
.
Задание 2.3.3 Определить свойство четности или нечетности функции 
а) функция четная;
б) функция нечетная;
в) свойствами четности и нечетности не обладает.
Задание 2.3.4 По графику функции определить четность или нечетность функции.
1) 
____________________________
2) 
____________________________
Задание 2.3.5 Дописать утверждение.
График четной функции симметричен относительно ____.График четной функции симметричен относительно ________.
Задание 2.3.6 Проверить на четность или нечетность функци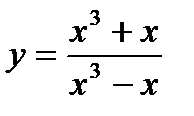и 
и 
.
1)___________2)___________
Задание 2.3.7 Привести примеры четной и нечетной функции.
Четные функции________________________________________________________
Нечетные функции______________________________________________________
