Симметричная нагрузка приемника

При симметричной системе напряжений и симметричной нагрузке, когда Z _a = Z _b = Z _c, т.е. когда R_a = R_b = R_c = R_ф и X_a = X_b = X_c = X_ф, фазные токи равны по значению и углы сдвига фаз одинаковы

I_a = I_b = I_c = I_ф = U_ф / Z_ф (3.12)

φ_a = φ_b = φ_c = φ = arctg (X_ф/R_ф) (3.13)

Построив векторную диаграмму токов для симметричного приемника (рис. 3.8), легко установить, что геометрическая сумма трех векторов тока равна нулю: İ_a + İ_b + İ_c = 0. Следовательно, в случае симметричной нагрузки ток в нейтральном проводе I_N = 0, поэтому необходимость в нейтральном проводе отпадает.

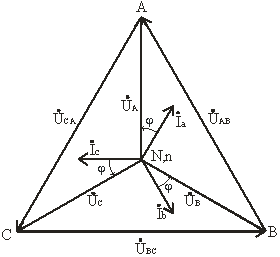
Рис. 3.8

При симметричной нагрузке

Z _ab = Z _bc = Z _ca = Z e^jφ (3.22)

т.е. Z_ab = Z_bc = Z_ca = Z, φ_ab = φ_bc = φ_ca = φ.

Так как линейные (они же фазные) напряжения U_AB, U_BC, U_CA симметричны, то и фазные токи образуют симметричную систему

İ_ab = Ú_ab / Z _ab; İ_bc = Ú_bc / Z _bc; İ_ca = Ú_ca / Z _ca.

Абсолютные значения их равны, а сдвиги по фазе относительно друг друга составляют 120°.

Линейные токи

İ_A = İ_ab - İ_ca; İ_B = İ_bc - İ_ab; İ_C = İ_ca - İ_bc;

образуют также симметричную систему токов (рис.3.13, 3.14).

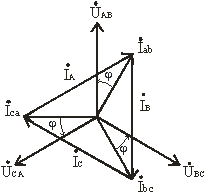
Рис. 3.13

На векторной диаграмме (рис. 3.14) фазные токи отстают от фазных напряжений на угол φ (полагаем, что фазы приемника являются индуктивными, т.е. φ > 0°). Здесь принято, что напряжение U_AB имеет нулевую фазу. Из диаграммы следует, что любой линейный ток больше фазного в 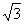раз. Линейный ток İ_Aотстает по фазе от фазного тока İ_ab на угол 30°, на этот же угол отстает İ_B от İ_bc, İ_C от İ_ca.

Таким образом, при соединении треугольником действующее значение линейного тока при симметричной нагрузке в 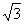раз больше действующего значения фазного тока и U_Л = U_Ф; I_Л = 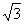I_Ф.

При равномерной нагрузке фаз расчет трехфазной цепи соединенной треугольником, можно свести к расчету одной фазы.

Фазное напряжение U_Ф = U_Л. Фазный ток I_Ф = U_Ф / Z_Ф, линейный ток I_Л = 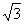I_Ф, угол сдвига по фазе φ = arctg (X_Ф / R_Ф).

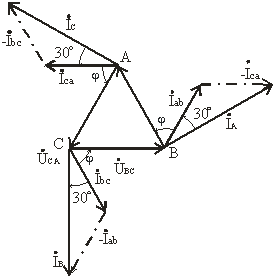
Рис. 3.14

 

Несимметричная нагрузка приемника

При симметричной системе напряжений и несимметричной нагрузке, когда Z_a ≠ Z_b ≠ Z_c и φ_a ≠ φ_b ≠ φ_cтоки в фазах потребителя различны и определяются по закону Ома

İ_a = Ú_a / Z _a; İ_b = Ú_b / Z _b; İ_c = Ú_c / Z _c.

Ток в нейтральном проводе İ_N равен геометрической сумме фазных токов

İ_N = İ_a + İ_b + İ_c.

Напряжения будут U_a = U_A; U_b = U_B; U_c = U_C, U_Ф = U_Л / 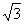, благодаря нейтральному проводу при Z_N = 0.

Следовательно, нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке.

Поэтому в четырехпроводную сеть включают однофазные несимметричные нагрузки, например, электрические лампы накаливания. Режим работы каждой фазы нагрузки, находящейся под неизменным фазным напряжением генератора, не будет зависеть от режима работы других фаз.

Векторная диаграмма при несимметричной нагрузке приведена на рис. 3.9

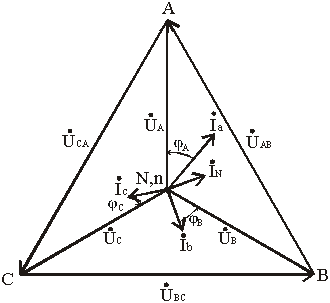
Рис. 3.9

Несимметричная нагрузка приемника:

В общем случае при несимметричной нагрузке Z_ab ≠ Z_bc ≠ Z_ca. Обычно она возникает при питании от трехфазной сети однофазных приемников. Например, для нагрузки, рис. 3.15, фазные токи, углы сдвига фаз и фазные мощности будут в общем случае различными.

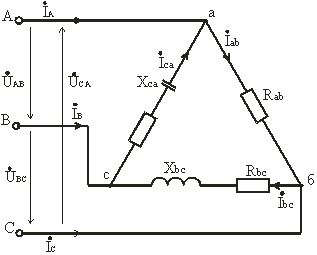
Рис. 3.15

Векторная диаграмма для случая, когда в фазе ab имеется активная нагрузка, в фазе bc – активно-индуктивная, а в фазе ca – активно-емкостная приведена на рис. 3.16, топографическая диаграмма – на рис. 3.17.

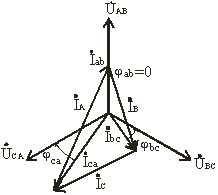
Рис. 3.16

Построение векторов линейных токов произведено в соответствии с выражениями

İ_A = İ_ab - İ_ca; İ_B = İ_bc - İ_ab; İ_C = İ_ca - İ_bc.

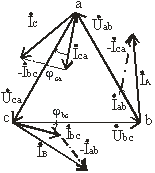
Рис. 3.17

Таким образом, при несимметричной нагрузке симметрия фазных токов İ_ab, İ_bс, İ_ca нарушается, поэтому линейные токи İ_A, İ_B, İ_C можно определить только расчетом по вышеприведенным уравнениям (3.20) или найти графическим путем из векторных диаграмм (рис. 3.16, 3.17).

Важной особенностью соединения фаз приемника треугольником является то, что при изменении сопротивления одной из фаз режим работы других фаз остается неизменным, так как линейные напряжения генератора являются постоянными. Будет изменяться только ток данной фазы и линейные токи в проводах линии, соединенных с этой фазой. Поэтому схема соединения треугольником широко используется для включения несимметричной нагрузки.

При расчете для несимметричной нагрузки сначала определяют значения фазных токов İ_ab, İ_bc, İ_ca и соответствующие им сдвиги фаз φ_ab, φ_bc, φ_ca. Затем определяют линейные токи с помощью уравнений (3.20) в комплексной форме или с помощью векторных диаграмм (рис. 3.16, 3.17).

Трехпроводная электрическая цепь.

Схема соединения источника и приемника звездой без нейтрального провода приведена на рис. 3.10.

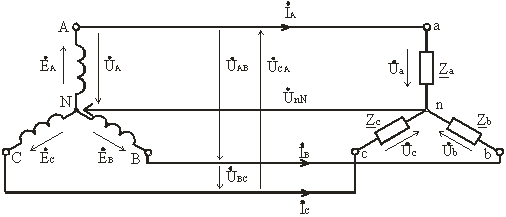
Рис. 3.10

При симметричной нагрузке, когда Z _a = Z _b = Z _c = Z_φ, напряжение между нейтральной точкой источника N и нейтральной точкой приемника n равно нулю, U_nN = 0.

Соотношение между фазными и линейными напряжениями приемника также равно 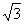, т.е. U_Ф = U_Л / 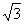, а токи в фазах определяются по тем же формулам (3.12, 3.13), что и для четырехпроводной цепи. В случае симметричного приемника достаточно определить ток только в одной из фаз. Сдвиг фаз между током и соответствующим напряжением φ = arctg (X / R).

При несимметричной нагрузке Z _a ≠ Z _b ≠ Z _c между нейтральными точками приемника и источника электроэнергии возникает напряжение смещения нейтрали U_nN.

Для определения напряжения смещения нейтрали можно воспользоваться формулой межузлового напряжения, так как схема рис 3.10 представляет собой схему с двумя узлами,

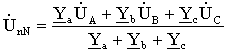(3.14)

где: Y _a = 1 / Z _a; Y _b = 1 / Z _b; Y _c = 1 / Z _c – комплексы проводимостей фаз нагрузки.

Очевидно, что теперь напряжения на фазах приемника будут отличаться друг от друга. Из второго закона Кирхгофа следует, что

Ú_a = Ú_A - Ú_nN; Ú_b = Ú_B - Ú_nN; Ú_c = Ú_C - Ú_nN (3.15)

Зная фазные напряжения приемника, можно определить фазные токи:

İ_a = Ú_a / Z _a = Y _a Ú_a; İ_b = Ú_b / Z _b = Y _b Ú_b; İ_c = Ú_c / Z _c = Y _c Ú_c (3.16)

Векторы фазных напряжений можно определить графически, построив векторную (топографическую) диаграмму фазных напряжений источника питания и U_nN (рис. 3.11).

При изменении величины (или характера) фазных сопротивлений напряжение смещений нейтрали U_nNможет изменяться в широких пределах. При этом нейтральная точка приемника n на диаграмме может занимать разные положения, а фазные напряжения приемника Ú_a, Ú_b и Ú_c могут отличаться друг от друга весьма существенно.

Таким образом, при симметричной нагрузке нейтральный провод можно удалить и это не повлияет на фазные напряжения приемника. При несимметричной нагрузке и отсутствии нейтрального провода фазные напряжения нагрузки уже не связаны жестко с фазными напряжениями генератора, так как на нагрузку воздействуют только линейные напряжения генератора. Несимметричная нагрузка в таких условиях вызывает несимметрию ее фазных напряжений Ú_a, Ú_b, Ú_c и смещение ее нейтральной точки n из центра треугольника напряжений (смещение нейтрали).

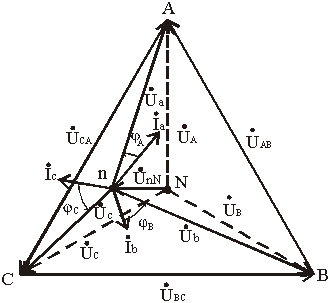
Рис. 3.11

Направление смещения нейтрали зависит от последовательности фаз системы и характера нагрузки.

Поэтому нейтральный провод необходим для того, чтобы:

· выравнивать фазные напряжения приемника при несимметричной нагрузке;

· подключать к трехфазной цепи однофазные приемники с номинальным напряжением в 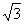раз меньше номинального линейного напряжения сети.

Следует иметь в виду, что в цепь нейтрального провода нельзя ставить предохранитель, так как перегорание предохранителя приведет к разрыву нейтрального провода и появлению значительных перенапряжений на фазах нагрузки.

 

3) При соединение фаз обмотки генератора (или трансформатора) звездой их концы X, Y и Z соединяют в одну общую точку N, называемую нейтральной точкой (или нейтралью) (рис. 3.6). Концы фаз приемников (Z_a, Z_b, Z_c) также соединяют в одну точку n. Такое соединение называется соединение звезда.

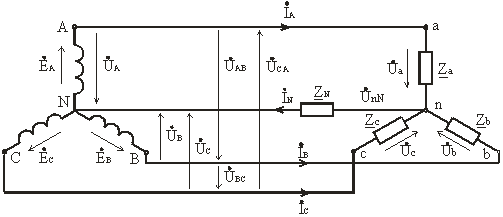
Рис. 3.6

Провода A − a, B − b и C − c, соединяющие начала фаз генератора и приемника, называются линейными, провод N − n, соединяющий точку N генератора с точкой n приемника, – нейтральным.

Трехфазная цепь с нейтральным проводом будет четырехпроводной, без нейтрального провода – трехпроводной.

В трехфазных цепях различают фазные и линейные напряжения. Фазное напряжение U _Ф – напряжение между началом и концом фазы или между линейным проводом и нейтралью (U_A, U_B, U_C у источника; U_a, U_b, U_c у приемника). Если сопротивлением проводов можно пренебречь, то фазное напряжение в приемнике считают таким же, как и в источнике. (U_A = U_a, U_B = U_b, U_C = U_c). За условно положительные направления фазных напряжений принимают направления от начала к концу фаз.

Линейное напряжение (U _Л) – напряжение между линейными проводами или между одноименными выводами разных фаз (U_AB, U_BC, U_CA). Условно положительные направления линейных напряжений приняты от точек, соответствующих первому индексу, к точкам соответствующим второму индексу (рис. 3.6).

По аналогии с фазными и линейными напряжениями различают также фазные и линейные токи:

· Фазные (I _Ф) – это токи в фазах генератора и приемников.

· Линейные (I _Л) – токи в линейных проводах.

При соединении в звезду фазные и линейные токи равны

I _Ф= I _Л (3.5)

Ток, протекающий в нейтральном проводе, обозначают I_N.

По первому закону Кирхгофа для нейтральной точки n (N) имеем в комплексной форме

İ _N =İ _A +İ _B +İ _C (3.6)

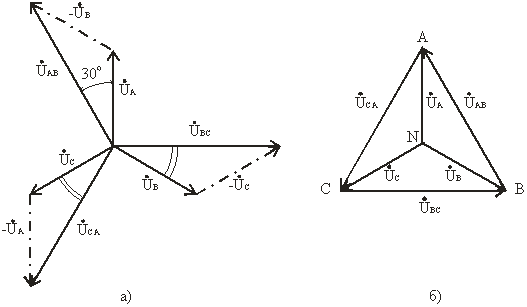
Рис. 3.7

В соответствии с выбранными условными положительными направлениями фазных и линейных напряжений можно записать уравнения по второму закону Кирхгофа.

Ú _AB =Ú _A −Ú _B; Ú _BC =Ú _B −Ú _C; Ú _CA =Ú _C −Ú _A (3.7)

Согласно этим выражениям на рис. 3.7а построена векторная диаграмма, из которой видно, что при симметричной системе фазных напряжений система линейных напряжений тоже симметрична: U_AB, U_BC, U_CA равны по величине и сдвинуты по фазе относительно друг друга на 120° (общее обозначение U _Л), и опережают, соответственно, векторы фазных напряжений U_A, U_B, U_C, (U _Ф) на угол 30°.

Действующие значения линейных напряжений можно определить графически по векторной диаграмме или по формуле (3.8), которая следует из треугольника, образованного векторами двух фазных и одного линейного напряжений:

U _Л=2 U _Фcos30°

или

U _Л= 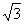U _Ф (3.8)

Предусмотренные ГОСТом линейные и фазные напряжения для цепей низкого напряжения связаны между собой соотношениями:

U _Л=660В; U _Ф=380В;
U _Л=380В; U _Ф=220В;
U _Л=220В; U _Ф=127В.

Векторную диаграмму удобно выполнить топографической (рис. 3.7б), тогда каждой точке цепи соответствует определенная точка на диаграмме. Вектор, проведенный между двумя точками топографической диаграммы, выражает по величине и фазе напряжения между одноименными точками цепи.

4) Несимметричная нагрузка приемника:

При симметричной системе напряжений и несимметричной нагрузке, когда Z_a ≠ Z_b ≠ Z_c и φ_a ≠ φ_b ≠ φ_cтоки в фазах потребителя различны и определяются по закону Ома

İ_a = Ú_a / Z _a; İ_b = Ú_b / Z _b; İ_c = Ú_c / Z _c.

Ток в нейтральном проводе İ_N равен геометрической сумме фазных токов

İ_N = İ_a + İ_b + İ_c.

Напряжения будут U_a = U_A; U_b = U_B; U_c = U_C, U_Ф = U_Л / 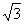, благодаря нейтральному проводу при Z_N = 0.

Следовательно, нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке.

Поэтому в четырехпроводную сеть включают однофазные несимметричные нагрузки, например, электрические лампы накаливания. Режим работы каждой фазы нагрузки, находящейся под неизменным фазным напряжением генератора, не будет зависеть от режима работы других фаз.

Векторная диаграмма при несимметричной нагрузке приведена на рис. 3.9

Рис. 3.9

5) Для расчета трехфазной цепи применимы все методы, используемые для расчета линейных цепей. Обычно сопротивления проводов и внутреннее сопротивление генератора меньше сопротивлений приемников, поэтому для упрощения расчетов таких цепей (если не требуется большая точность) сопротивления проводов можно не учитывать (Z_Л = 0, Z_N = 0). Тогда фазные напряжения приемника U_a, U_b и U_c будут равны соответственно фазным напряжениям источника электрической энергии(генератора или вторичной обмотки трансформатора), т.е. U_a = U_A; U_b = U_B; U_c = U_C. Если полные комплексные сопротивления фаз приемника равны Z _a = Z _b = Z _c, то токи в каждой фазе можно определить по формулам

İ_a = Ú_a / Z _a; İ_b = Ú_b / Z _b; İ_c = Ú_c / Z _c (3.10)

В соответствии с первым законом Кирхгофа ток в нейтральном проводе

İ_N = İ_a + İ_b + İ_c = İ_A + İ_B + İ_C (3.11)

6) Трехпроводная электрическая цепь:

Схема соединения источника и приемника звездой без нейтрального провода приведена на рис. 3.10.

Рис. 3.10

При симметричной нагрузке, когда Z _a = Z _b = Z _c = Z_φ, напряжение между нейтральной точкой источника N и нейтральной точкой приемника n равно нулю, U_nN = 0.

Соотношение между фазными и линейными напряжениями приемника также равно 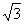, т.е. U_Ф = U_Л / 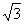, а токи в фазах определяются по тем же формулам (3.12, 3.13), что и для четырехпроводной цепи. В случае симметричного приемника достаточно определить ток только в одной из фаз. Сдвиг фаз между током и соответствующим напряжением φ = arctg (X / R).

При несимметричной нагрузке Z _a ≠ Z _b ≠ Z _c между нейтральными точками приемника и источника электроэнергии возникает напряжение смещения нейтрали U_nN.

Для определения напряжения смещения нейтрали можно воспользоваться формулой межузлового напряжения, так как схема рис 3.10 представляет собой схему с двумя узлами,

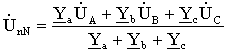(3.14)

где: Y _a = 1 / Z _a; Y _b = 1 / Z _b; Y _c = 1 / Z _c – комплексы проводимостей фаз нагрузки.

Очевидно, что теперь напряжения на фазах приемника будут отличаться друг от друга. Из второго закона Кирхгофа следует, что

Ú_a = Ú_A - Ú_nN; Ú_b = Ú_B - Ú_nN; Ú_c = Ú_C - Ú_nN (3.15)

Зная фазные напряжения приемника, можно определить фазные токи:

İ_a = Ú_a / Z _a = Y _a Ú_a; İ_b = Ú_b / Z _b = Y _b Ú_b; İ_c = Ú_c / Z _c = Y _c Ú_c (3.16)

Векторы фазных напряжений можно определить графически, построив векторную (топографическую) диаграмму фазных напряжений источника питания и U_nN (рис. 3.11).

При изменении величины (или характера) фазных сопротивлений напряжение смещений нейтрали U_nNможет изменяться в широких пределах. При этом нейтральная точка приемника n на диаграмме может занимать разные положения, а фазные напряжения приемника Ú_a, Ú_b и Ú_c могут отличаться друг от друга весьма существенно.

Таким образом, при симметричной нагрузке нейтральный провод можно удалить и это не повлияет на фазные напряжения приемника. При несимметричной нагрузке и отсутствии нейтрального провода фазные напряжения нагрузки уже не связаны жестко с фазными напряжениями генератора, так как на нагрузку воздействуют только линейные напряжения генератора. Несимметричная нагрузка в таких условиях вызывает несимметрию ее фазных напряжений Ú_a, Ú_b, Ú_c и смещение ее нейтральной точки n из центра треугольника напряжений (смещение нейтрали).

Рис. 3.11

Направление смещения нейтрали зависит от последовательности фаз системы и характера нагрузки.

Поэтому нейтральный провод необходим для того, чтобы:

· выравнивать фазные напряжения приемника при несимметричной нагрузке;

· подключать к трехфазной цепи однофазные приемники с номинальным напряжением в 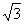раз меньше номинального линейного напряжения сети.

Следует иметь в виду, что в цепь нейтрального провода нельзя ставить предохранитель, так как перегорание предохранителя приведет к разрыву нейтрального провода и появлению значительных перенапряжений на фазах нагрузки.