Штучний нейрон – це складова частина штучної нейронної мережі (рис. 2.1).
До складу нейрона входять помножувачі (синапси), суматор і нелінійний перетворювач. Синапси здійснюють зв'язок між нейронами і перемножають вхідний сигнал на число, яке характеризує силу зв'язку – вагу синапсу.
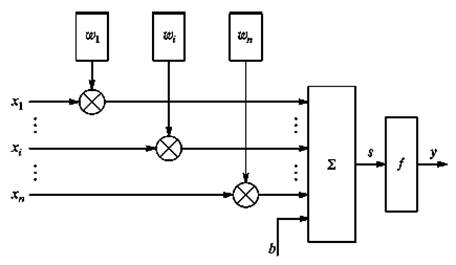
Рис. 2.2. Структура штучного нейрона
Суматор складає сигнали, що поступають по синаптичних зв'язках від інших нейронів, і зовнішніх вхідних сигналів. Нелінійний перетворювач реалізує нелінійну функцію одного аргументу – виходу суматора. Ця функція називається «функція активації» або «передавальна функція» нейрона. Нейрон в цілому реалізує скалярну функцію векторного аргументу. Математична модель нейрона описується співвідношеннями:
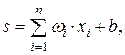(2.1)
де: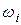 
– вага синапсу 
; 
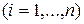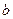– значення зміщення;
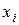– компонента вхідного вектору (вхідний сигнал) ;
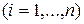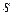- результат додавання; у – вихідний сигнал нейрона;
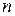- число входів нейрона;
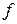- нелінійне перетворення (функція активації або передаточна функція).
У загальному випадку вхідний сигнал, вагові коефіцієнти і значення зсуву можуть приймати дійсні значення. Вихід (у) визначається видом функції активації і може бути як дійсним, так і цілим (табл.2.1). У багатьох практичних задачах входи, вага і зсуви можуть приймати лише деякі фіксовані значення.
Синаптичні зв'язки із позитивними вагами називають збуджуючими, з негативними масами – гальмуючими.
Таким чином, нейрон повністю описується своїми вагами 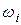і передаточною функцією f(s). Одержавши набір чисел (вектор) хі, нейрон видає деяке число у на виході.
Таблиця 2.1. Перелік функцій активації нейронів
| Назва | Формула | Область значень |
| Порогова |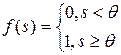 
| (0, 1) |
| Знакова (сигнатурна) |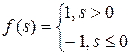 
| (-1, 1) |
| Сигмоїдальна (логістична) |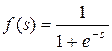 
| (0, 1) |
| Напівлінійна |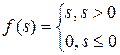 
| (0, ¥) |
| Лінійна | f(s) = s | (-¥, ¥) |
| Радіальна базисна (гаусівська) |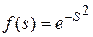 
| (0, 1) |
| Гіперболічний тангенс |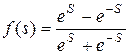 
| (-1, 1) |
Описаний обчислювальний елемент (2.1) можна вважати спрощеною математичною моделлю біологічних нейронів – клітин, з яких складається нервова система людини і тварин.
Щоб підкреслити відмінність нейронів біологічних і математичних, їх іноді називають нейроноподібними елементами або формальними нейронами.
На вхідний сигнал (s) нелінійний перетворювач відповідає вихідним сигналом f(s), який є виходом нейрона у. Приклади активаційних функцій представлені у таблиці 2.1 і на рисунку. 2.3.
Однією з найпоширеніших є нелінійна функція з насиченням, так звана логістична функція або сигмоід (тобто функція S-подібного вигляду):
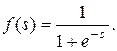(2.2)
При зменшенні а сигмоід стає більш пологим, в межах при а=0 вироджуючись в горизонтальну лінію на рівні 0,5, при збільшенні а сигмоїд наближається до вигляду функції одиничного стрибка з порогом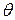 
в точці s=0. Із виразу для сигмоїда очевидно, що вихідне значення нейрона лежить у діапазоні [0, 1]. Одна з цінних властивостей сигмоідної функції – простий вираз для її похідної:
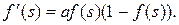(2.3)
Слід зазначити, що сигмоїдна функція диференційована на всій осі абсцис. Крім того вона має властивість посилювати слабкі сигнали краще, ніж великі, і запобігає насиченню від великих сигналів, оскільки вони відповідають областям аргументів, де сигмоїд має пологий нахил.
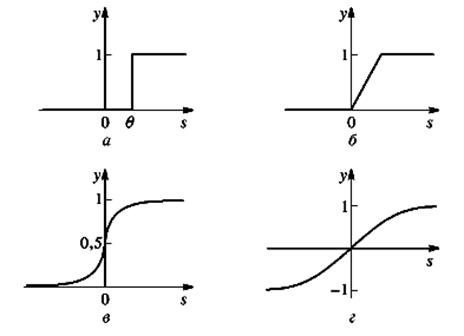
Рис. 2.3. Приклади активаційних функцій: а – функція одиничного стрибка;
б – лінійний поріг (гістерезис); в – сигмоїд (гіперболічний тангенс);
г – сигмоїд (логістична)
Повертаючись до загальних рис, властивих всім НМ, відзначимо принцип паралельної обробки сигналів, який досягається шляхом об'єднання великого числа нейронів у так звані шари і з'єднання певним чином нейронів різних шарів, а також, в деяких конфігураціях, і нейронів одного шару між собою, причому обробка взаємодії всіх нейронів ведеться пошарово.
Контрольні питання
1. Дайте визначення штучного нейрона
2. Наведіть структуру та спрощену математичну модель штучного нейрона
3. Що таке активаційна функція?
4. Наведіть активаційні функції
