Контрольная работа состоит из двух частей: теоретической и практической.
Теоретическая часть выполняется в виде ответа на теоретический вопрос согласно варианту.
Практическая часть заключается в решении практической задачи.
Вариант для выполнения данной контрольной работы выбирается следующим образом: две последние цифры зачетной книжки студента складываются и сумме прибавляется единица. Полученное число является номером варианта.
Структура контрольной работы:
1. Титульный лист.
2. Содержание.
3. Ответ на теоретический вопрос.
4. Описание выполнения практических заданий.
5. Список литературы.
Текст должен быть представлен в редакторе Word, cтраницы работы должны быть пронумерованы, на каждой из них справа оставлены поля размером 2,5-3 см для замечаний и предложений рецензента, шрифт - 14, одинарный межстрочный интервал. В конце реферата приводится список использованной литературы, ставится подпись и дата выполнения.
Вопросы для выполнения теоретической части задания
1. Процесс принятия решения. Стили и методы.
2. Эконометрические методы принятия решений.
3. Задачи теории расписаний.
4. Детерминированные модели принятия решений. Задачи линейного программирования. Основные постановки ЗЛП. Примеры.
5. Динамическое программирование как метод оптимизации. Примеры.
6. Принятие решений в условиях неопределенности.
7. Теория ожидаемой полезности.
8. Постановка задачи стохастического программирования.
9. Математическое моделирование при принятии решений.
10. Системы поддержки принятия решений.
11. Сетевое планирование.
12. Принятие решений - работа менеджера.
13. Процедура подстраивающегося победителя — метод решения задач принятия решений
14. Игровые модели принятия решений. Основные понятия теории игр. Определение игры. Разновидности игровых моделей. Примеры.
15. Дискретные задачи размещения
16. Антагонистические игры. Критерий существования седловой точки в антагонистической игре. Принцип гарантированного результата.
17. Матричные игры. Свойства оптимальных стратегий игроков в матричной игре. Эквивалентные задачи линейного программирования.
18. Биматричная игра. Методы исследования кооперативных игр.
19. Теория решения изобретательских задач.
Перечень основной и дополнительной учебной литературы
В обязательном порядке следует указывать ссылки на ресурсы электронных библиотечных систем, доступных для использования в ДИТИ НИЯУ МИФИ!
| N п/п | Автор | Название | Место издания | Наименование издательства | Год издания | Количество экземпляров | ||
| Основная литература | ||||||||
| Кулик, С.Д. | Элементы теории принятия решений (критерии и задачи) [Электронный ресурс]: учебное пособие для вузов | М | НИЯУ МИФИ | |||||
| Голубева Н.В. | . Математическое моделирование систем и процессов: учебное пособие | СПб | Лань | |||||
| Дополнительная литература | ||||||||
| Дегтярёв Ю. И.. | Исследование операций: учебник для вузов по специальности АСУ. | М | Высшая школа | |||||
| Вентцель Е.С. | Исследование операций. Задачи, принципы, методология | М | Наука | |||||
| Грешилов А. А. | Математические методы принятия решений. | М: | МГТУ им. Н.Э. Баумана | |||||
| Афанасьев М.Ю., Суворов Б.П | Исследование операций в экономике: модели, задачи, решения: Учеб. пособие | М | ИНФРА-М, | |||||
Перечень ресурсов информационно-телекоммуникационной сети «Интернет»
http://e.lanbook.com/view/book/4406/page163
http://e.lanbook.com/view/book/10250/page4
http://e.lanbook.com/view/book/49465/page292
http://e.lanbook.com/view/book/52398/page3
http://www.iqlib.ru/errors/firefox/noscript.html
Практическое задание. Принятие решений в условиях определенности
Вариант 1
Собственные средства банка в сумме с депозитами составляют 200 млн. руб. Часть этих средств, но не менее 30 млн. руб. должна быть размещена в кредитах, не менее 35 % средств, размещенных в кредитах и ценных бумагах, составляют ценные бумаги. Доходность кредитов – 20%, ценных бумаг – 15%.
Распределить средства банка между кредитами и ценными бумагами, чтобы получить максимальный доход.
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Практическое задание. Принятие решений в условиях определенности
Вариант № 2
Предприятию необходимо выпустить 3 вида продукции в количестве 300, 500 и 100 ед. соответственно. Для этого используется 3 вида станков Т1, Т2, Т3, каждый из которых может обрабатывать любое из трех изделий. Запас мощности станков (рабочее время) составляет соответственно 40,60 и 30 ед. времени.
Производительность каждого станка для каждого изделия и себестоимость каждого изделия при обработке на каждом станке приводятся в таблице:
| станок | производительность | себестоимость | ||||
| 1 изд. | 2 изд. | 3 изд. | 1 изд. | 2 изд. | 3 изд. | |
| Т1 | 1,5 | |||||
| Т2 | 1,7 | 3,3 | ||||
| Т3 | 2,5 |
Составить план загрузки станков, который соответствует минимальной себестоимости изделий.
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Практическое задание. Принятие решений в условиях определенности
Вариант 3
Небольшая фирма выпускает два типа автомобильных деталей (А и В). Для этого она закупает литье, подвергаема товарной обработки, сверловки и шлифовки. Данные, характеризующие производительность станочного парка фирмы, даны в таблице:
| Станки | Деталь А шт/час | Деталь В шт/час |
| Токарный | ||
| Сверлильный | ||
| Шлифовальный |
Каждая отливка, из которой изготавливают деталь А, стоит 60 руб. Стоимость отливки для детали В–90 руб. Продажная цена деталей равна соответственно 150 и 180 руб. Стоимость часа станочного времени составляет по трем типам станков 600, 420 и 510 руб. соответственно.
Найти план выпуска продукции, максимизирующий прибыль.
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Практическое задание. Принятие решений в условиях определенности
Вариант 4
Для производства трех видов продукции предприятие использует два типа технологического оборудования и два вида сырья. Нормы затрат сырья и времени на изготовление одного изделия каждого вида приведены в таблице. В ней же указаны общий фонд рабочего времени каждой из групп технологического оборудования, объёмы имеющегося сырья каждого вида, а также цена одного изделия данного вида и ограничения на возможный выпуск каждого из изделий.
Составить такой план производства продукции, согласно которому будет изготовлено необходимое количество изделий каждого вида, а общая стоимость всей изготовляемой продукции максимальна.
| Ресурсы | Нормы затрат на одно изделие вида | Общее количество ресурсов | ||
| Производительность оборудования (нормо-ч): I типа | - | |||
| II типа | ||||
| Сырье (кг): 1-го вида | ||||
| 2-го вида | ||||
| Цена одного изделия (руб.) | - | |||
| Выпуск (шт.): минимальный | - | |||
| максимальный | - |
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Практическое задание. Принятие решений в условиях определенности
Вариант 5
При производстве четырех видов кабеля выполняется пять групп технологических операций. Нормы затрат на 1 км кабеля данного вида на каждой из групп операций, прибыль от реализации 1 км каждого вида кабеля, а также общий фонд рабочего времени, в течение которого могут выполняться эти операции, указаны в таблице.
| Технологическая операция | Нормы затрат времени (ч) на обработку 1 км кабеля вида | Общий фонд рабочего времени (ч) | |||
| Волочение | 1,2 | 1,8 | 1,6 | 2,4 | 7 200 |
| Наложение изоляций | 1,0 | 0,4 | 0,8 | 0,7 | 5 600 |
| Скручивание элементов в кабель | 6,4 | 5,6 | 6,0 | 8,0 | 11 176 |
| Освинцование | 3,0 | - | 1,8 | 2,4 | 3 600 |
| Испытание и контроль | 2,1 | 1,5 | 0,8 | 3,0 | 4 200 |
| Прибыль от реализации 1 км кабеля (руб.) | 1,2 | 0,8 | 1,0 | 1,3 |
Определить такой план выпуска кабеля, при котором общая прибыль от реализации изготовляемой продукции является максимальной.
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Вариант 6
Изготовляемый на пяти кирпичных заводах кирпич поступает на шесть строящихся объектов. Ежедневное производство кирпича и потребность в нем указаны в таблице. В ней же указана цена перевозки 1000 шт. кирпича с каждого из заводов к каждому из объектов.
| Кирпичный завод | Цена перевозки 1 тыс. шт. кирпича к строящемуся объекту | Производство кирпича (тыс. шт.) | |||||
| I | |||||||
| II | |||||||
| III | |||||||
| IV | |||||||
| V | |||||||
| Потребность в кирпиче (тыс.шт.) |
Составить план перевозок, согласно которому обеспечиваются потребности в кирпиче на каждом из строящихся объектов при минимальной общей стоимости перевозок.
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Вариант 7
Для обогрева помещений используют четыре агрегата, каждый из которых может работать на любом из пяти сортов топлива, имеющемся в количествах 90, 110, 70, 80 и 150 т. Потребность в топливе каждого из агрегатов соответственно равна 80, 120, 140 и 160 т. Теплотворная способность i- го сорта топлива при использовании его на j- м агрегате задаётся матрицей
.
Найти такое распределение топлива между агрегатами, при котором получается максимальное количество теплоты от использования всего топлива.
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Практическое задание. Принятие решений в условиях определенности
Вариант 8
На ткацкой фабрике для изготовления трёх артикулов ткани используются ткацкие станки двух типов, пряжа и красители. В таблице указаны производительность станков каждого типа, нормы расхода пряжи и красителей, цена 1 м ткани данного артикула, а также общий фонд рабочего времени станков каждого типа, имеющиеся в распоряжении фабрики фонды пряжи и красителей и ограничения на возможный выпуск тканей данного артикула.
| Ресурсы | Нормы затрат на 1 м ткани артикула | Общее количество ресурсов | ||
| Производительность станков (станко-ч): I типа | 0,02 | - | 0,04 | |
| II типа | 0,04 | 0,03 | 0,01 | |
| Пряжа (кг) | 1,0 | 1,5 | 2,0 | |
| Красители (кг) | 0,03 | 0,02 | 0,025 | |
| Цена 1 м ткани (руб.) | - | |||
| Выпуск ткани (м): минимальный | - | |||
| максимальный | - |
Составить такой план изготовления тканей, согласно которому будет произведено нужное количество тканей данного артикула, а общая стоимость всех тканей максимальна.
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Практическое задание. Принятие решений в условиях определенности
Вариант 9
На швейной фабрике для изготовления четырёх видов изделий может быть использована ткань трёх артикулов. Нормы расхода тканей всех артикулов на пошив одного изделия приведены в таблице. В ней же указаны имеющиеся в распоряжении фабрики общее количество тканей каждого артикула и цена одного изделия данного вида. Определить, сколько изделий каждого вида должна произвести фабрика, чтобы стоимость изготовленной продукции была максимальной.
| Артикул ткани | Норма расхода ткани (м) на одно изделие вида | Общее количество ткани (м) | |||
| I | - | ||||
| II | - | ||||
| III | - | ||||
| Цена одного изделия (руб.) |
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Практическое задание. Принятие решений в условиях определенности
Вариант 10
Предприятие выпускает четыре вида продукции и использует три типа основного оборудования: токарное, фрезерное и шлифовальное. Затраты времени на изготовление единицы продукции для каждого из типов оборудования приведены в таблице. В ней же указаны общий фонд рабочего времени каждого из типов оборудования, а также прибыль от реализации одного изделия данного вида. Определить такой объем выпуска каждого из изделий, при котором общая прибыль от их реализации является максимальной.
| Тип оборудования | Затраты времени (станко-ч) на единицу продукции вида | Общий фонд рабочего времени (ч) | |||
| Токарное | |||||
| Фрезерное | - | ||||
| Шлифовальное | - | ||||
| Прибыль от реализации единицы продукции (руб.) | |||||
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Практическое задание. Принятие решений в условиях определенности
Вариант 11
Торговое предприятие планирует организовать продажу четырёх видов товара (А, В, С и D), используя при этом только два вида ресурсов: рабочее время продавцов в количестве 840ч и площадь торгового зала 180м2.
При этом известны плановые нормативы затрат этих ресурсов в расчёте на единицу товаров А, В, С и D и прибыль от их продажи, которые приведены в таблице:
| Показатели | Товар | Общее количество ресурсов | |||
| А | В | С | D | ||
| Расход рабочего времени на единицу товара (ч) | 0,6 | 0,8 | 0,6 | 0,4 | |
| Использование площади торгового зала на единицу товара (м2) | 0,1 | 0,2 | 0,4 | 0,1 | |
| Прибыль от продажи единицы товара (руб.) |
Требуется определить оптимальную структуру товарооборота, обеспечивающую торговому предприятию максимум прибыли.
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Практическое задание. Принятие решений в условиях определенности
Вариант 12
На мебельной фабрике изготовляется пять видов продукции: столы, шкафы, диваны-кровати, кресла-кровати и тахты. Нормы затрат труда, а также древесины и ткани на производство единицы продукции данного вида приведены в таблице.
| Ресурсы | Нормы расхода ресурса на единицу продукции | Общее количество ресурсов | ||||
| стол | шкаф | диван-кровать | кресло-кровать | тахта | ||
| Трудозатраты (человеко-ч) | ||||||
| Древесина (м3) | 0,4 | 0,6 | 0,3 | 0,2 | 0,3 | |
| Ткань (м) | - | - | ||||
| Прибыль от реализации одного изделия (руб.) | - | |||||
| Выпуск (шт.): минимальный | - | |||||
| максимальный | - |
В этой же таблице указана прибыль от реализации одного изделия каждого вида, приведено общее количество ресурсов данного вида, имеющееся в распоряжении фабрики, а также указано (на основе изучения спроса), в пределах каких объёмов может изготовляться каждый вид продукции.
Определить план производства продукции мебельной фабрикой, согласно которому прибыль от ее реализации является максимальной. Одновременно необходимо провести после оптимизационный анализ решения задачи.
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Практическое задание. Принятие решений в условиях определенности
Вариант 13
Необходимо составить план развития каждого из m предприятий, выпускающих однородную продукцию. Число возможных вариантов развития i -го предприятия различно и равно ni. Реализация j -го варианта развития i -го предприятия (j = 
) требует капитальных затрат, равных Kij, и обеспечивает выпуск продукции в объеме bij единиц. При этом экономический эффект от капитальных вложений на развитие i -го предприятия по j- му варианту равен cij. Учитывая, что необходимо выпустить продукцию в количестве B единиц и что общая величина капиталовложений ограничена и равна K, составить такой план развития предприятий, при котором экономический эффект от реализации выбранных вариантов развития предприятий является максимальным.
;
B=1000; K=100 000 000
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Практическое задание. Принятие решений в условиях определенности
Вариант 14
На звероферме могут выращиваться черно-бурые лисицы и песцы. Для обеспечения нормальных условий их выращивания используется три вида кормов. Количество корма каждого вида, которое должны ежедневно получать лисицы и песцы, приведено в таблице. В ней же указаны общее количество корма каждого вида, которое может быть использовано зверофермой, и прибыль от реализации одной шкурки лисицы и песца.
| Вид корма | Количество единиц корма, которое ежедневно должны получать | Общее количество корма | |
| лисица | песец | ||
| I | |||
| II | |||
| III | |||
| Прибыль от реализации одной шкурки (руб.) | |||
Определить, сколько лисиц и песцов следует выращивать на звероферме, чтобы прибыль от реализации их шкурок была максимальной
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Практическое задание. Принятие решений в условиях определенности
Вариант 15
Для выполнения четырёх видов землеройных работ могут быть использованы экскаваторы четырёх типов. Производительность экскаватора i -го типа при выполнении j -й работы задаётся матрицей.
Учитывая, что на каждой из работ может быть занят только лишь один экскаватор и что все экскаваторы должны быть задействованы, найти такое распределение экскаваторов между работами, которое обеспечивает максимальную производительность.
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Практическое задание. Принятие решений в условиях определенности
Вариант 16
Пароход может быть использован для перевозки 11 наименований груза, масса, объем и цена единицы каждого из которых приведены в таблице:
| Параметры единицы груза | Номер груза | ||||||||||
| Масса (т) | |||||||||||
| Объем (м3) | |||||||||||
| Цена (тыс.руб) | 4,4 | 2,7 | 3,2 | 2,8 | 2,7 | 2,8 | 3,3 | 3,5 | 4,7 | 3,9 | 4,0 |
На пароход может быть погружено не более 800 т груза общим объёмом, не превышающим 600 м3. Определить, сколько единиц каждого груза следует поместить на пароход так, чтобы общая стоимость размещённого груза была максимальной.
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Практическое задание. Принятие решений в условиях определенности
Вариант 17
Из листового проката нужно выкроить заготовки четырёх видов. Один лист длиной 184 см можно разрезать на заготовки длиной 45,50,65 и 85 см. Всего заготовок каждого вида необходимо соответственно 90,96,88 и 56 шт. Способы разреза одного листа на заготовки и величина отходов при каждом способе приведены в таблице:
| Длина заготовки (см) | Количество заготовок, выкраиваемых из одного листа при разрезе способом | ||||||||||||
| - | - | - | - | - | |||||||||
| - | - | - | - | - | |||||||||
| - | - | - | - | - | - | - | |||||||
| - | - | - | - | - | - | - | - | - | - | ||||
| Величина отходов (см) |
Определить, какое количество листов по каждому из способов следует разрезать, чтобы получить нужное количество заготовок данного вида при минимальных общих отходах.
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Практическое задание. Принятие решений в условиях определенности
Вариант 18
Для производства трёх видов изделий предприятие использует три вида сырья. Нормы расхода каждого вида сырья определяются матрицей
Предприятие может использовать сырья I вида не более 20 ед., II вида – не более 42 ед., III вида - не более 36 ед. Цена единицы продукции каждого вида линейно зависит от некоторого параметра t, эта зависимость соответственно имеет вид 2 +t, 12 – t, 6 + t(0 
). Для каждого значения параметра t(0 
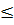t 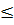10) найдите такой план выпуска продукции, реализация которого обеспечивает максимальный выпуск изделий в стоимостном выражении.
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
Практическое задание. Принятие решений в условиях определенности
Вариант 19
Для производства трёх видов изделий А, В и С предприятие использует четыре вида сырья. Нормы затрат сырья каждого вида на производство единицы продукции данного вида приведены в таблице. В ней же указана прибыль от реализации одного изделия каждого вида. Изделия А, В и С могут производиться в любых соотношениях (сбыт обеспечен), но для их производства предприятие может использовать сырья I вида не более 200 кг, II вида – не более 120 кг, III вида – не более 180 кг, IV вида – не более 138 кг. Определите: а) план производства продукции, при котором общая прибыль предприятия от реализации всей продукции была бы наибольшей; б)устойчивость оптимального плана задачи относительно изменений прибыли от реализации единицы изделия данного вида; в)устойчивость оптимального плана задачи относительно изменения количества сырья вида.
Построить математическую модель задачи. Решить полученную задачу вручную, средствами MS EXCEL или в любом математическом приложении.
Интерпретировать полученное решение математической задачи как решение исходной задачи.
