(А.П.Чехов – водевиль «Свадьба»)
…истинно говорю вам,
если не обратитесь и не будете как дети,
не войдете в Царство Небесное
(Мф. 18:3)
Вот бегает дворовый мальчик,
В салазки жучку посадив,
Себя в коня преобразив …
(А.С.Пушкин «Евгений Онегин»)
*************************************************************************************
Поиграем в «буковки» по правилам:
 (1)
(1)
Игра состоит в том, что во всех предложенных выражениях или текстах, где встречаются «буковки» x и y, мы всюду вместо x будем писать a∙x'+b∙y', а вместо y – p∙x'+q∙y', совершая попутно всякие разумные преобразования буквенных выражений, как если бы они были составлены не из букв, а из чисел. Например, вместо ab (если надо) будем писать ba, вместо (a+b)c будем писать ac+bc или наоборот (опять же, если надо или если захочется) и т.д. В результате мы получим новое, как говорят, преобразованное выражение или текст, или ещё иногда говорят о «варианте текста», который бывает очень любопытно сравнить с исходным...
То, что текст изменится, это понятно (потому его и называют вариантом):
например, в нём уже не будет букв x и y, а будут новые буквы – x' и y'.
Но ведь любой текст должен выражать какой-то внутренний смысл и, значит, обладать структурой. Так может быть структура в целом или какие-то её «отдельности» останутся неизменными или, как говорят, инвариантными, если не по факту, то по смыслу?
Вот поиск таких инвариантов и составит содержание предлагаемой игры в преобразования.
В качестве примера рассмотрим преобразование квадратичной формы (КФ)
Ax2 + 2Bxy + Cy2 = (2)
=A(a x' +b y')2+2B(a x' +b y')(p x' +q y')+C(p x '+q y')2=
= A(a2 x' 2+2ab x'y' +b2 y' 2)+
+2B(ap x '2+(aq+bp) x'y' +bq y' 2)+
+C(p2 x' 2+2pq x'y' +q2 y' 2) =
= (Aa2+2Bap+Cp2)x'2+
+2(Aab+B(aq+bp)+Cpq)x'y'+
+(Ab2+2Bbq+Cq2)y'2 ≡
≡ A'x'2+2B'x'y'+C'y'2, (3)
где
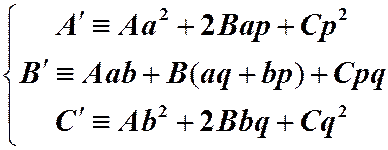 (4)
(4)
Здесь в левой части каждого равенства стоят
«смыслы»: « являются новыми коэффициентами»,
являются новыми коэффициентами»,
а в правой – «факты», свидетельствующие об истории возникновения этих «смыслов».
Таким образом квадратичная форма (2) сохраняет свой вид (пример «качественного» инварианта!) и в новых координатах (3) при условии, что коэффициенты пересчитываются по формулам (4).
Естественно поставить вопрос: а может ли наш «качественный» инвариант сохраняться и «количественно»? Точнее говоря, как надо сузить общность преобразования (1), или, что то же самое, как надо ограничить произвольность выбора чисел a, b, p, q, чтобы сохранялись и коэффициенты квадратичной формы (2)? То есть, чтобы было 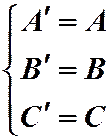 (5)
(5)
Ответ на этот вопрос даёт следующая
ТЕОРЕМА:
Если  , где aq−bp= 1, (6)
, где aq−bp= 1, (6)
то квадратичная форма
−px2 + (a−q)xy + by2 (7)
инвариантна вместе со всеми своими коэффициентами.
То же будет верно и для обратного преобразования
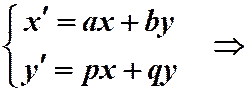
 (6')
(6')
при условии

ЗАМЕЧАНИЕ 1: Обратное преобразование мы получили из (1) естественным образом: новые (правые) буквы мы стали считать старыми (и потому лишили штрихов), а старые (левые) буквы стали рассматривать как новые (и для обозначения этого украсили их штрихами). Затем мы разрешили
полученные равенства относительно заново изготовленных старых букв и получили (6').
ЗАМЕЧАНИЕ 2: Сравнивая (3) и (7) мы должны заметить, что
в случае (7) A ≡ −p; B ≡ ½(a−q); C ≡ b. (8)






