***************************************************
Таким образом, если
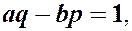
то целая бесконечная группа преобразований
имеет инвариантами коэффициенты квадратичной формы −px2 + (a−q)xy + by2
ЗАМЕЧАНИЕ 1:
ЗАМЕЧАНИЕ 2: Наблюдая, за продолжением цепочки (9) – (10), можно увидеть, что группа «кратных» преобразований G содержит подгруппу «2-кратных», «3-кратных» и т.д. преобразований.
ЗАМЕЧАНИЕ 3: Поскольку преобразование с инвариантом всегда сопровождается группой порождённых им кратных преобразований, то мы, говоря определённо об одном преобразовании, будем представлять себе не всю группу, не какое-то произвольное преобразование из группы, но именно то линейное преобразование, которое (вместе со своим обратным и тождественным) конструирует всю группу G.
******************************************************************
У нас было: A ≡ −p; B ≡ ½(a−q); C ≡ b. (8)
и aq−bp = 1. 
Теперьрассмотренную «игру в буковки» можно переформулировать так: каковы должны быть a,b,p,q, чтобы
коэффициенты КФAx2+2Bxy+Cy2 были инвариантны
Иными словами, теперь нужно a,b,p,q выразить через A, B и C.
Имеем
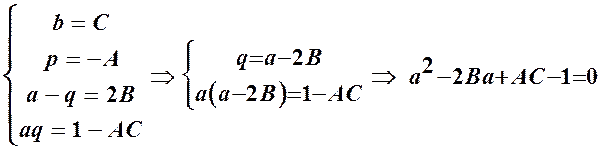
Значит, искомое преобразование должно иметь вид:
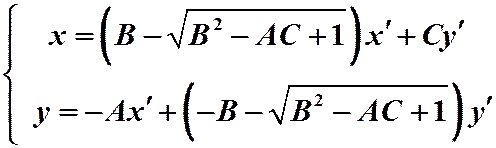(11)
или
(12)
В результате этих преобразований
Ax2+2Bxy+Cy2 = Ax'2 + 2Bx'y'+Cy'2 (13)
ЗАМЕЧАНИЕ 1: Из (11) и (12), в частности, следует, что не любая КФ имеет линейное преобразование, оставляющее инвариантными её коэффициенты, но лишь та, у которой В2−АС +1 ≥ 0. (14)
ЗАМЕЧАНИЕ 2: Было бы соблазнительно проверить, а не являются ли
преобразования (11) и (12) взаимно-обратными? К сожалению, это не так, и
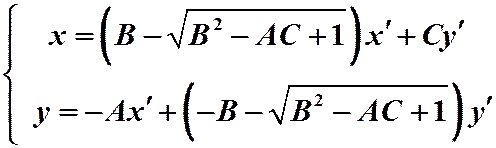(11)
и
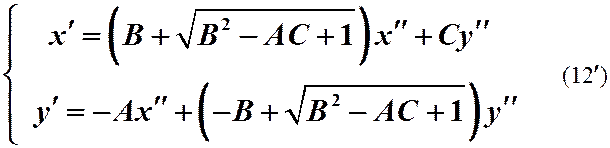
уводят нас
в «зазеркалье»:
Конечно, при повторениии эти преобразования вернут нас из «зазеркалья», но это уже другая история.
ЗАМЕЧАНИЕ 3
Итак каждой КФ (13), то есть тройке чисел А, В и С, удовлетворяющих условию (14), соответствует ровно два линейных преобразования (11) и (12), однозначно определяемых параметрами
А, В и С.
Иными словами, и КФ, и преобразование при их однозначной (в каждой своей из двух ветвей) связи имеют три «степени свободы»
Ограничим теперь общность исследования рассмотрением случая В = 0.
На «идеи» это принципиально не повлияет, а вычисления заметно упростит.
Итак если (см.(14)) АС ≤1, то преобразование (см. (12))
(15)
оставит инвариантными (неизменными) коэффициенты КФ
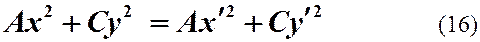
При этом теперь уже для каждой пары чисел А и С существуют
два однозначно определяемых по формулам (15) преобразования.
Рассмотрим одно из них:
(17)
Ещё раз отметим, что (16) и (17) имеют две степени свободы и
взаимно-однозначную зависимость. Если теперь мы ослабим условие (16)
и потребуем инвариантности от несколько другой КФ, а именно:
то для сохранения есть целая степень свободы в выборе преобразования (меньше ограничений – больше возможностей, разумеется, при прочих равных условиях). Рассмотрим по отдельности три возможных случая:
I. C = Ac2 II. A/C = 0 III. C = −Ac2
__________________________________
I. ГЕОМЕТРИЯ ЕВКЛИДА
Подставив C = Ac2 в (18) и (17), убедимся, что КФ
(19)
инвариантна относительно всех преобразований вида
,
которые можно переписать так:
или так:
, (20)
где 
.
ВЫВОД: Преобразование (20), сохраняя инвариантной форму (19), представляет собой композицию деформации (вдоль оси x
в с раз) и поворота на угол 
. Инвариантность КФ, записанной в виде 
, утверждает сохранение расстояний.
II. ГЕОМЕТРИЯ ГАЛИЛЕЯ
Подставив в (17) A = 0, получим
преобразование Галилея:
,
которое мы привыкли видеть в несколько других обозначениях:
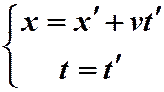. (21)
Здесь одна (одномерная) система отсчётаК' движется вдоль другой, неподвижной системы отсчёта К со скоростью v.
Инвариантность КФ y 2 = y' 2 т.е. 
является непосредственным следствием второго уравнения (21)
и утверждает абсолютность времени (одинаковость хода часов во всех системах отсчёта).
_________________________________________
III. ГЕОМЕТРИЯ ЭЙНШТЕЙНА
Подставив C = −Ac2 в (17), получим для инвариантности КФ 
семейство преобразований
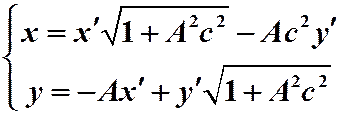, (22)
зависящее от параметра А. Как правило, вместо параметра А вводят параметр v с помощью соотношения
. (23)
Выразим отсюда А:
(24)
Подставив теперь (23) и (24) в (22), получим:
(25)
Чтобы перейти к физическому истолкованию инвариантности КФ
и обеспечивающих эту инвариантность преобразований (25), перепишем их в общепринятом виде,
в котором они называются преобразованиями Лоренца:
(26)
которые интерпретируются следующим образом.
Подвижная система отсчёта К' (числовая ось x' с часами t') скользит вдоль неподвижной системы отсчёта К (числовая ось x с часами t) с постоянной скоростью v. В подтверждение этого обратимся к первому уравнению из (26): чтобы x было нулём, то есть, чтобы быть неподвижным относительно К, находясь в К', надо в К' двигаться со скоростью x'/t'=−v.
Следующий момент: преобразования Лоренца возникли из требования инвариантности
КФ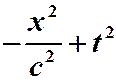 
. (27)
Инвариантность (27) означает, в частности, что
,
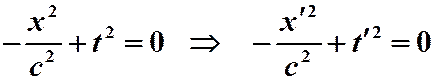то есть
(28)
иными словами, если существует нечто, распространяющееся волнообразно в обе стороны систем отсчёта с некоторой постоянной скоростью с, причём – скоростью, одинаковой для всех систем отсчёта, движущихся друг относительно друга с различными скоростями, то координаты и времена (относящиеся к двум системам отсчёта К' и К, движущихся друг относительно друга со скоростью v, если смотреть из К, и со скоростью «− v», если наблюдать из К') должны преобразовываться по Лоренцу, откуда, в частности, следует, что движения со скоростями v, большими с, запрещены, а сама скорость с является максимальной скоростью
распространения взаимодействий.
