Когда говорят об измерении углов на местности, то имеют в виду не сами величины углов, образованных в общем случае наклонными направлениями с наблюдаемых пунктов на выбранные пункты (цели, ориентиры), а углы между проекциями этих направлений на горизонтальную плоскость при измерении горизонтальных углов или на вертикальную плоскость при измерении вертикальных углов и углов наклона (рис.2.14).
Именно эти углы необходимы для вычисления взаимного положения пунктов А и Б на земной поверхности в определенной системе координат.
Так, если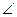 
АОВ - угол на местности между наклонными направлениями ОА и ОВ, то его горизонтальная проекция 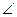А'ОВ' получится в результате проецирования точек А и В на горизонтальную плоскость (точки А' и В'). Мерой этого угла будет линейный угол β, называемый горизонтальным углом.
Для получения превышений между пунктами на земной поверхности АОВ проецируется на вертикальную плоскость (точки А" и В). Полученный угол x называется вертикальным углом.
Угол в вертикальной плоскости, образованный горизонтальной плоскостью, проходящей через точку О, и направлением на какой-либо объект, называется углом наклона. На рис.2.14 показаны два угла наклона:
- для направления ОА - 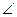γА;
- для направления О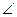В - γВ.
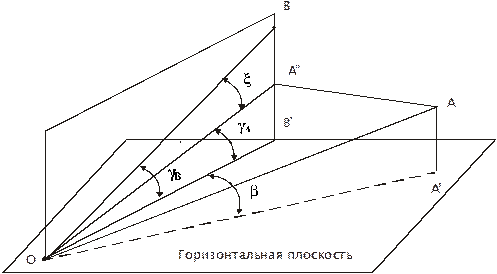
Рис.2.14. Горизонтальный и вертикальный углы
Переход от дирекционного угла одного направления к дирекционному углу другого направления
От дирекционного угла одного направления к дирекционному углу другого направления, исходящих из одной и той же точки, переходят при вычислениях теодолитных (буссольных) ходов, прямых и обратных засечек, определении дирекционного угла продольной оси топопривязчика (машины), а также при выполнении графических построений и измерений на карте (планшете).
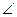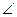Пусть с точки А (рис.2.15) известен дирекционный угол (АС) направления на точку С, и на этой же точке А измерены два горизонтальных угла 1 и 2.
Требуется определить дирекционные углы (АВ) и (АD) с точки А на точки В и D, которые называют соответственно левым и правым относительно биссектрисы измеренного угла.
|
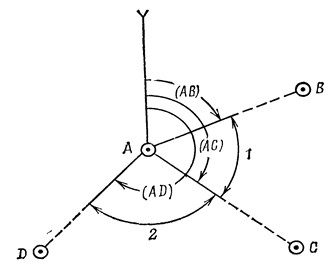
Из рис.2.15 следует, что дирекционный угол правого направления
(АD) = (АС) + 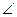2,
дирекционный угол левого направления
(АВ) = (АС) - 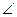1.
На этом основании можно сформулировать следующие правила вычисления дирекционных углов:
1. Дирекционный угол правого направления равен дирекционному углу левого направления плюс горизонтальный угол между ними. Если полученная сумма будет больше 360о (60-00), то из нее вычитают 360о (60-00).
2. Дирекционный угол левого направления равен дирекционному углу правого направления минус горизонтальный угол между ними. Если исходный дирекционный угол меньше значения горизонтального угла, то к нему прибавляют 360 о (60-00).
Пример 2.4
Известен дирекционный угол
(АD) = 282о35'46"
и измерены углы: 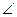1 = 102о15'42";
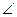2 = 85о12'32"; 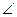3 = 172о31'46".
Вычислить дирекционные углы (АВ) и
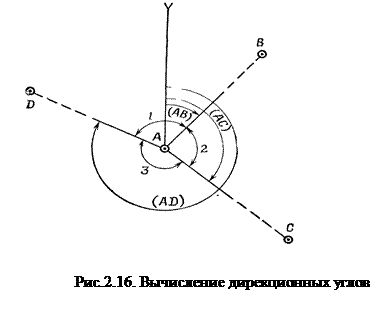
(АС) (рис.2.16).
Решение
Каждый из определяемых дирекционных углов может быть вычислен через дирекционный угол (АD) двумя способами.
Первый способ:
1. (АВ) = (АD) + 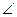1.
(АВ) = 282о35'46" + 102о15'42" = 384о51'28" = 24о51'28".
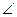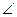2. (АВ) = (АD) - ( 2 + 3).
(АВ) = 282о35'46" - (172о31'46" + 85о12'32") = 24о51'28".
Второй способ:
1. (АC) = (АD) + 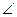3.
(АC) =282о35'46" - 172о31'46" = 110о04'00".
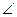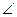2. (АC) = (АD) + 1 + 2.
(АC) = 282о35'46" + 102о15'42" + 85о12'32" = 470о04'00".
(АC) = 470о04'00" - 360о00'00" = 110о04'00".
Рассмотренные правила можно заменить одним, если измерять горизонтальные углы по ходу часовой стрелки от направления, дирекционный угол которого известен, до определяемого направления.
