Задача 1. Первая партия из 15 одинаковых изделий, среди которых 2 изделия бракованных. Во второй партий 20 таких же изделий, из которых 3 бракованных. Наудачу взятое изделие из первой партии переложено во вторую, после чего из второй партии выбирается наугад одно изделие. Определить вероятность того, что выбранное изделие окажется бракованным.
Решение: Задача решается по формуле полной вероятности.
Обозначим: Событие А - выбранное (после перекладывания) из второй партии изделие бракованное;
Событие 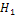 , - переложено бракованное изделие из 1-ой партии во 2-ую. Событие
, - переложено бракованное изделие из 1-ой партии во 2-ую. Событие  - переложено не бракованное изделие из 1-ой партии во 2-ую. Вероятность событий
- переложено не бракованное изделие из 1-ой партии во 2-ую. Вероятность событий 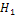 , и
, и  находим по ситуации для первой партии, откуда и берется изделие для перекладывания. Очевидно:
находим по ситуации для первой партии, откуда и берется изделие для перекладывания. Очевидно:  .
.
Сумма этих вероятностей равна 1, так как события 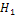 , и
, и  составляет полную группу событий. Во второй партии после перекладывания будет 21 изделие, причем число бракованных среди них будет зависеть от того, какое изделие мы переложим.
составляет полную группу событий. Во второй партии после перекладывания будет 21 изделие, причем число бракованных среди них будет зависеть от того, какое изделие мы переложим.
Очевидно: 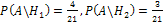 . По формуле полной вероятности находим:
. По формуле полной вероятности находим: 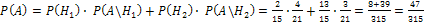 .
.
Ответ: 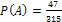 .
.
Задача 2. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй - 84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом.
Решение: Обозначим через А событие - деталь отличного качества. Можно сделать два предположения (гипотезы): В, - деталь произведена первым автоматом, причем (поскольку первый автомат производит вдвое больше деталей, чем второй) 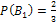 ; В2 – деталь произведена вторым автоматом, причем
; В2 – деталь произведена вторым автоматом, причем 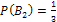 .
.
Условная вероятность того, что деталь будет отличного качества, если она произведена первым автоматом, Р(А\В) = 0,6. Условная вероятность того, что деталь будет отличного качества, если она произведена вторым автоматом, Р(А\В2) = 0,84. Вероятность того, что наудачу взятая деталь окажется отличного качества, по формуле полной вероятности равна:
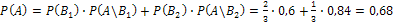 .
.
Искомая вероятность того, что взятая отличная деталь произведена первым автоматом, по формуле Байеса равна:
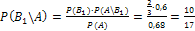 .
.
Ответ: 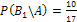 .
.






