Задача 1. В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?
Решение: Общее число различных исходов есть 
= 1000. Число исходов благоприятствующих получению выигрыша, составляет 
= 200.
Согласно формуле, получим
.
Ответ: 
.
Задача 2. Из корзины, в которой находятся 12 белых и 8 черных шаров, вынимают наудачу два шара. Какова вероятность того, что оба шара окажутся черными?
Решение: Обозначим событие, состоящее в появлении двух черных шаров, через А. Общее число возможных случаев равно числу сочетаний из 20 элементов (12+8) по два: 
.
Число случаев , благоприятствующих событию А, составляет 
. По формуле 
находим вероятность появления двух черных шаров: 
Ответ: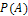 
= 0,147.
Задача 3. В партии из 18 деталей находятся 4 бракованных. Наугад выбирают 5 деталей. Найти вероятность того, что из этих 5 деталей две окажутся бракованными.
Решение: Число всех равновозможных независимых исходов равно числу сочетаний из 18 по 5, то есть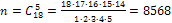 
.
Подсчитаем число исходов , благоприятствующих событию А. Среди 5 взятых наугад деталей должно быть 3 качественных и 2 бракованных. Число способов выборки двух бракованных деталей из 4имеющихся бракованных равно числу сочетаний из 4 по 2: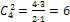 
.
Число способов выборки трех качественных деталей из 14 имеющихся качественных равно 
. Любая группа качественных деталей может комбинироваться с любой группой бракованных деталей, поэтому общее число комбинаций т составляет 
. Искомая вероятность события 
равна отношению числа исходов , благоприятствующих этому событию, к числу всех равновозможных независимых исходов: 
.
Ответ: вероятность того, что из 5 деталей 5 окажутся бракованными, равна 0,255.
