Сфера применения орграфов еще больше расширяется, если использовать не знаковые, а взвешенные орграфы. Во взвешенном орграфе каждой дуге присваивается не знак, а коэффициент, больший или меньший единицы (со своим знаком). Импульсная или абсолютная устойчивость взвешенного орграфа предупреждает о том, что в системе что-то не в порядке, необходимо изменить структуру системы (добавить новые вершины, удалить или добавить дуги, изменить коэффициенты) или провести искусственное регулирование.
Особенностью многокомпонентных задач является то, что с помощью орграфов удается объединить в модели системы различные социальные, экономические и экологические показатели. Часть этих показателей может иметь статистическую базу, другая часть — не иметь, а третья — оцениваться качественно. С помощью решения многокомпонентных задач можно оценить тенденцию развития системы, что, безусловно, ценно. Но при уточнении модели можно сформировать количественный прогноз изменения показателей системы, а также найти различные варианты воздействия на изучаемую систему с целью получения лучшего варианта.
До сих пор рассматривались ориентированные графы, в которых единственной количественной характеристикой является весовой коэффициент (или знак) на дуге. Для прогнозирования экосистем этого недостаточно, поскольку специалистов может интересовать вопрос не только о том, какой будет система, но и в какие сроки система достигнет того или иного состояния. В этом случае необходимо каждой дуге поставить в соответствие не только коэффициент, определяющий влияние одного показателя на другой, но и задержку реализации изменения одного показателя в ответ на изменение другого. Если эта задержка равна нулю, то изменение показателя будет произведено мгновенно; если же указан определенный интервал времени, то изменение показателя будет произведено только по прошествии указанного интервала времени. Эти возможности еще более усиливают применяемый математический аппарат и делают его привлекательнее.
Рассмотрим простейший пример, в котором используются временные задержки. На рис. 13.18 представлен орграф модели развития промышленного центра и состояния окружающей среды. В нем даны весовые коэффициенты и время задержки реализации воздействия одного показателя на другой, выраженное в годах.

Рис. 13.18. Взвешенный орграф с временными задержками для изучения
развития промышленного центра и состояния окружающей среды
В результате моделирования на основе данного взвешенного орграфа с временными задержками можно получить тенденцию изменения показателей в привязке к оси времени. Полученный график представлен на рис. 13.19.
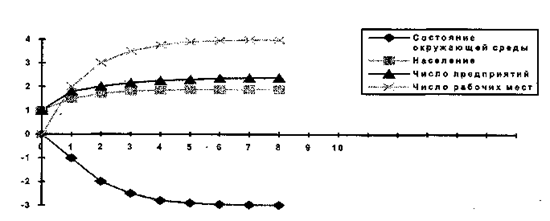
Рис. 13.19. Изменение показателей в соответствии с результатами
моделирования на основе орграфа, представленного на рис. 13.18
При разработке модели на базе орграфа можно использовать статистические методы. Однако статистические данные по показателям, всесторонне характеризующим социо-эколого-экономическую систему, отсутствуют. Поэтому для формирования ориентированного графа и определения весов на его дугах следует воспользоваться методами экспертных оценок.






