Принципиальная схема лабораторной установки представлена на рис.6. Она состоит из диска массой md, закрепленных на нем четырех стержней массами m2, и четырех грузов массами m1, расположенных симметрично на стержнях. На диск намотана нить, к которой подвешен груз массой m.
Согласно второму закону Ньютона составим уравнение поступательного движения груза m без учета сил трения:
|
| Рис.6. |
(25)
или в скалярном виде, т.е. в проекциях на направление движения:
. (26)
Откуда
, (27)
где T – сила натяжения нити. Согласно основному уравнению динамики вращательного движения (24), момент силы T, под действием которой система тел md, m1, m2 совершает вращательное движение, равен произведению момента инерции I этой системы на ее угловое ускорение b:
или 
, (28)
где R – плечо этой силы равное радиусу диска.
Выразим силу натяжения нити из (28):
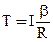(29)
и приравняем правые части (27) и (29):
. (30)
Линейное ускорение связано с угловым следующим соотношением a=bR, следовательно:
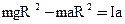. (31)
Откуда ускорение груза m без учета сил трения в блоке равно:
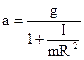. (32)
Рассмотрим динамику движения системы с учетом сил трения, которые действуют в системе. Они возникают между стержнем, на котором закреплен диск и неподвижной частью установки (внутри подшипников), а также между подвижной частью установки и воздухом. Все эти силы трения мы будем учитывать с помощью момента сил трения.
С учетом момента сил трения уравнение динамики вращения записывается следующим образом:
, (33)
где a’ – линейное ускорение при действии сил трения, Mтр – момент сил трения.
Вычитая уравнение (33) из уравнения (28), получим:
,
. (34)
Ускорение без учета силы трения (а) можно рассчитать по формуле (32). Ускорение гирьки с учетом сил трения можно рассчитать из формулы для равноускоренного движения, измерив пройденный путь S и время t:
. (35)
Зная значения ускорений (а и а’), по формуле (34) можно определить момент сил трения. Для расчетов необходимо знать величину момента инерции системы вращающихся тел, который будет равен сумме моментов инерции диска, стержней и грузов.
Момент инерции диска согласно (14) равен:
. (36)
Момент инерции каждого из стержней (рис.6) относительно оси О согласно (16) и теореме Штейнера равен:
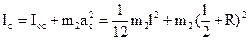, (37)
где ac=l/2+R, R – расстояние от центра масс стержня до оси вращения О; l – длина стержня; Ioc – его момент инерции относительно оси, проходящей через центр масс.
Аналогично рассчитываются моменты инерции грузов:
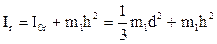, (38)
где h – расстояние от центра масс груза до оси вращения О; d – длина груза; I0r – момент инерции груза относительно оси, проходящей через его центр масс. Сложив моменты инерции всех тел, получим формулу для вычисления момента инерции всей системы:
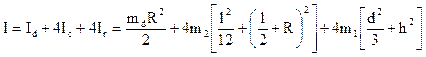. (39)
