При начислении простых процентов наращенная сумма определяется по формуле
S = P (1 + i t), (1)
где S – наращенная сумма (стоимость), ден.ед.; P – первоначальная сумма (стоимость), ден.ед.; i – процентная ставка, выраженная в коэффициенте; t – период начисления процентов.
Начисление простых процентов осуществляется в случае, когда начисленные проценты не накапливаются на сумму основного долга, а периодически выплачиваются, например, раз в год, полугодие, в квартал, в месяц и т. д., что определяется условиями кредитного договора. Также на практике встречаются случаи, когда расчеты производятся за более короткие периоды, в частности на однодневной основе.
В случае, когда срок ссуды (вклада и т. д.) менее одного года, в расчетах необходимо скорректировать заданную процентную ставку в зависимости от временного интервала. Например, можно представить период начисления процентов (t) в виде отношения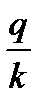 
, где q – число дней (месяцев, кварталов, полугодий и т. д.) ссуды; k – число дней (месяцев, кварталов, полугодий и т. д.) в году.
Таким образом, формула (1) изменяется и имеет следующий вид:
S = P (1 + i 
). (2)
В зависимости от количества дней в году возможны различные варианты расчетов. В случае, когда за базу измерения времени берут год, условно состоящий из 360 дней (12 месяцев по 30 дней), исчисляют обыкновенные, или коммерческие проценты. Когда за базу берут действительное число дней в году (365 или 366 – в високосном году), говорят о точных процентах.
При определении числа дней пользования ссудой также применяется два подхода: точный и обыкновенный. В первом случае подсчитывается фактическое число дней между двумя датами, во втором – месяц принимается равным 30 дням. Как в первом, так и во втором случае, день выдачи и день погашения считаются за один день. Также существуют случаи, когда в исчислении применяется количество расчетных или рабочих банковских дней, число которых в месяц составляет 24 дня.
Таким образом, выделяют четыре варианта расчета:
1. обыкновенные проценты с точным числом дней ссуды;
2. обыкновенные проценты с приближенным числом дней ссуды;
3. точные проценты с приближенным числом дней ссуды;
4. точные проценты с банковским числом рабочих дней.
При этом необходимо учесть, что на практике день выдачи и день погашения ссуды (депозита) принимают за один день.
