од ’эмминга относитс€ к кодам, которые позвол€ют не только обнаруживать но и исправл€ть одиночные ошибки.
»справл€ющую способность кода достигаетс€ за счет многократных проверок на четность определенных групп разр€дов. L Ц число информационных разр€дов кода. K Ц контрольный разр€д. N = L + K Ц их общее число.
ѕо результатам проверок на четность любого числа групп из k Ц контрольных разр€дов можно получить  различных двоичных комбинаций.
различных двоичных комбинаций.
ќбщее число одиночных ошибок, которое может быть в n Ц разр€дах, в том числе отсутствие ошибок дает нам n + 1 указание на число ошибок и их отсутствие.  .
.
1. L=1 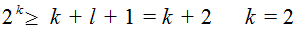 код Ђ1 из 3ї.
код Ђ1 из 3ї.
000 Ц 0
111 Ц 1

| 
| 
|
| X | X | |
| X | X |
0 0 0 - 0
1 1 1 - 1
Ётот код имеет  , позвол€ет исправл€ть м
, позвол€ет исправл€ть м  ,
,

| 
| 
|
| X | X | |
| X | X |
 0
0
1
1 1 1
≈сли k = 3 то L: 
ѕолучаетс€ код Ђ4 из 7ї.

| 
| 
| 
| 
| 
| 
|
| x | x | x | x | |||
| x | x | x | x | |||
| x | x | x | x |
L=11 K=4 N=15 Ђ11 из 15ї
L=26 K=5 N=31 Ђ26 из 31ї
»спользуетс€ дл€ оптимизации кодировани€, при котором часто встречающиес€ символы кодируютс€ с малым числом разр€дов, а редко встречающиес€ кодируютс€ с большим количеством разр€дов, при этом средн€€ нагрузка на любой разр€д становитс€ одинаковой дл€ всех символов. ¬ обычном двоичном неизбыточном коде все разр€ды считаютс€ равноверо€тными и кодовые комбинации из n разр€дов в среднем числа 0 и 1 одинаковы.
¬еро€тность по€влени€ нул€ P(0) = P(1) = ½.
ѕо формуле ’артли количество информации в этой комбинации 
ѕри n разр€дов 






