Рассмотрим некоторые алгоритмы порождения (перечисления) последовательности всех перестановок п элементов.
а) Лексикографическая (алфавитная). Последовательность определяется индуктивно: для каждой перестановки указан первый элемент, далее - все следующие за ним.
1, (все перестановки из {2,..., n} в алфавитном порядке)
2, (все перестановки из {1, 3,..., n} в алфавитном порядке).
3, (все перестановки из (1, 2, 4,..., n} в алфавитном порядке)
n, (все перестановки из (1, 2,,.,, n -1} в алфавитном порядке).
б) Конфигурации (перестановки) располагаются в такой последовательности, что каждая (начиная со второй) отличается от предыдущей тем, что в ней поменялись местами ровно два элемента (такая ситуация и вместе с тем операция такой замены называется транспозицией).
в) Частным случаем предыдущего можно считать последовательность, в которой разница между двумя соседними перестановками еще меньше: они различаются транспозицией двух соседних элементов.
§1.4. Приложения к теории вероятностей и теоретической физике.
Припишем исходу х. некоторое число 
где 
- действительное число, 
этому числу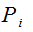 
будем придавать вероятностный смысл и 
равно вероятности появления этого исхода. Будем считать, что все элементы 
равновероятны могут 
Если при этом мы считаем за сопутствующее нашему опыту m, то вероятность этого будет 
.
