1. Ребро е произвольного графа G называется циклическим, если оно принадлежит хотя бы одному элементарному циклу в графе, и ациклическим в противном случае.
Справедливы два простых утверждения:
1) при удалении из связного графа циклического ребра граф остается связным;
2) при удалении ациклического ребра граф становится несвязным.
Связный граф без циклов называется деревом.
Иначе говоря, дерево - это граф, все ребра которого ациклические. Имеется несколько эквивалентных определений дерева:
1) связный граф, который становится несвязным при удалении любого ребра;
2) связный граф, у которого число ребер на единицу меньше числа вершин;
3) граф, любые две вершины которого связаны единственной элементарной цепью;
4) граф без циклов, в котором после добавления ребра, связывающего две любые вершины, появляется цикл.
2. Выберем в дереве произвольную вершину 
назовем ее корнем, или вершиной нулевого яруса. Соседние вершины назовем вершинами первого яруса и т.д. - вершины, соседние вершинам (i -1)-го яруса, не отнесенные еще ни к одному ярусу, назовем вершинами i-гo яруса. Каждая вершина дерева принадлежит ровно одному ярусу.
Очевидно, что номер яруса совпадает с расстоянием между его вершинами и корнем дерева. В силу свойства (3) каждая вершина i-ro яруса связана ребром ровно с одной вершиной (i - 1)-го яруса и не связана ребром ни с какой вершиной i-ro яруса (рис. 2.5). Такое представление дерева в виде графа показывает, что в конечном дереве всегда существуют концевые вершины (например, вершины последнего яруса, но, возможно, и другие).
Выделение корня в дереве D определяет на множестве его вершин частичный порядок: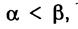 
если 
и элементарная цепь из корня в вершину β содержит α. Корень α0 является единственным минимальным элементом в этом частично упорядоченном множестве вершин, а все концевые вершины (исключая корень: он может быть, но может и не быть концевой вершиной) - максимальными. Каждая вершина α однозначно определяет корневое поддерево 
натянутое на множество таких вершин β что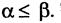 
В каждом таком поддереве 
(в том числе в 
) можно выделить вершины, непосредственно подчиненные корню поддерева т.е. такие вершины что не существует промежуточных вершин между ними. Для каждой такой вершины определим ветвь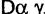 
как корневое поддерево 
как корневое поддерево с корнем α, натянутое на множество вершин α. Все поддерево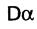 
получается из своих ветвей склеиванием их в корне 
3. В связном графе Gбудем последовательно удалять циклические ребра до тех пор, пока это возможно, т.е. пока не останется ни одного циклического ребра. Мы придем к связному подграфу графа G с тем же множеством вершин, но без элементарных циклов, т.е. к дереву, называемому остовом графа G. Остов выбирается неоднозначно, однако все ациклические ребра обязательно входят в любой остов. Относительно остова D все ребра подграфа G называются хордами. Каждая хорда связывает две вершины остова.
На рис. 2.7а - пример остова (его ребра выделены) графа с 11 вершинами и 18 ребрами. Последовательность циклов и удаляемых из них ребер представлены в таблице 2.1. Оставшиеся ребра, образующие остов: 2, 3, 4, 7, 10, 11, 12, 15, 17, 18.
Удаление из дерева концевого ребра вместе с концевой вершиной приводит к связному графу без элементарных циклов, т.е. к дереву, содержащему на одну вершину и на одно ребро меньше, чем исходное дерево. Продолжая этот процесс, мы придем (если исходное дерево конечно) к дереву, состоящему из одного ребра (и двух его вершин). Поскольку из исходного дерева удалено одинаковое число ребер и вершин, то можно сделать вывод:
