Каждому с детства привычен способ записи чисел в десятичной системе. Эта система называется позиционной десятичной, потому что натуральное число представляется словом в алфавите из десяти
арабских цифр  , причем знаки числа изображают
, причем знаки числа изображают
различные его составляющие в зависимости от разряда - позиции в числе и служат коэффициентами при степенях 10. Например,
48087 = 40000 + 8000 + 80 + 7 = 4-Ю4+8-103+0-102+8-10'+7-10°, и цифра 8 во втором разряде изображает число 80, а та же цифра в четвертом разряде - число 8000. Позиционная система исторически
вытеснила другие способы представления чисел благодаря удобствам использования, главным образом, из-за достаточно простых алгоритмов арифметических действий над многозначными числами, которые сводятся к действиям над однозначными числами. При этом используются таблица сложения, т.е. правила типа 3+6=9, 4+8=12 и т.п., общеизвестная таблица умножения и - при сложении и умножении столбиком - правила переноса десятков в старшие разряды ("шестью девять - пятьдесят четыре; четыре пишем, пять в уме"). Отметим, что при сложении столбиком справа налево двух слагаемых каждый очередной знак суммы определяется знаками слагаемых в этом разряде с учетом знака переноса (0, если сумма не превышает 9, или 1, если сумма
двузначная). При умножении многозначных чисел Ах В столбиком каждое умножение А на однозначное число, каким является очередной
разряд числа В, также сопровождается переносом числа десятков в следующий разряд. Далее следует сложение нескольких многозначных чисел, записываемых со сдвигом. При сложении большого количества чисел может возникать накопление знаков переноса. Важно заметить, что как при сложении, так и при умножении каждый знак результата зависит от знаков слагаемых/сомножителей, находящихся в том же разряде и правее, и не зависит от старших разрядов (находящихся левее). Так, младший разряд результата является функцией двух однозначных чисел - младших разрядов слагаемых/сомножителей. Второй справа разряд есть функция 4 однозначных переменных - знаков двух младших разрядов слагаемых/сомножителей и т.д.
Таким же образом, только много проще, устроена двоичная система счисления. Числа представляются словами в алфавите
 и, например,
и, например,  =
=
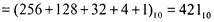 (подстрочные индексы 2 и 10
(подстрочные индексы 2 и 10
обозначают, что одно число записано в двоичной, а другое - в десятичной системе). Вот двоичные представления нескольких первых натуральных чисел (в левом столбце - десятичные; в правом -двоичные):

Подобно тому, как в десятичной системе счисления целые степени основания системы 10 записываются единицей с нулями, а число на 1
меньшее - 99...9, в двоичной системе число 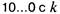 нулями изображает
нулями изображает
число 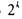 , а число 11...1 из k единиц равно
, а число 11...1 из k единиц равно 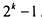
Таблица сложения для двоичных чисел чрезвычайно проста: 0 + 0 = 0; 0+1 = 1+0=1; 1 + 1 = 10. Таблица умножения еще проще:
0x0 = 0x1 = 1x0-0; 1x1 = 1.
Их можно представить и таблицами с двумя входами:
Отсюда  - простота действий над многозначными числами, хотя двоичная запись числа длиннее десятичной более, чем втрое. Предыдущий пример демонстрирует перевод двоичного числа в десятичное. Для этого, так же как и для обратного перехода полезно знать значения целых степеней числа 2: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 и т.д. Например, 179 = 128 + 51 = 27 +32 +19 = = 27 + 25 + 16 + 3 = 27 + 25 + 24 + 2 + 1 поэтому двоичная запись числа 179 - 10110011 (слагаемые 26,23,22 входят в сумму 179 с коэффициентом 0, остальные степени 2-е коэффициентом 1). Ниже -примеры арифметических действий над двоичными числами (параллельно приведены действия с теми же числами в десятичной записи).
- простота действий над многозначными числами, хотя двоичная запись числа длиннее десятичной более, чем втрое. Предыдущий пример демонстрирует перевод двоичного числа в десятичное. Для этого, так же как и для обратного перехода полезно знать значения целых степеней числа 2: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 и т.д. Например, 179 = 128 + 51 = 27 +32 +19 = = 27 + 25 + 16 + 3 = 27 + 25 + 24 + 2 + 1 поэтому двоичная запись числа 179 - 10110011 (слагаемые 26,23,22 входят в сумму 179 с коэффициентом 0, остальные степени 2-е коэффициентом 1). Ниже -примеры арифметических действий над двоичными числами (параллельно приведены действия с теми же числами в десятичной записи).
Как 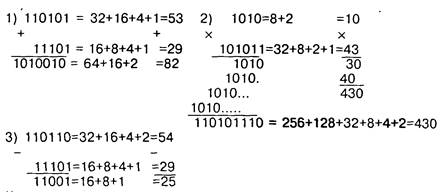 видим, сложение, вычитание и умножение многозначных двоичных чисел производится так же, как и для десятичных, в частности, в обеих системах k -и знак результата арифметических действий зависит от
видим, сложение, вычитание и умножение многозначных двоичных чисел производится так же, как и для десятичных, в частности, в обеих системах k -и знак результата арифметических действий зависит от 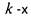 знаков слагаемых/сомножителей и знаков младших разрядов.
знаков слагаемых/сомножителей и знаков младших разрядов.
Однако накопление знаков переноса при сложении возникает здесь значительно чаще: каждые две единицы дают перенос одной единицы в следующий - старший - разряд, сложение четырех единиц дает две единицы переноса, т.е. перенос одной единицы на два разряда влево.
Деление двоичных чисел "столбиком" также намного проще, чем в десятичной системе, поскольку не приходится подбирать очередной знак [
частного, остаток не должен быть меньше делителя, - в этом случае знак частного 1; в противном случае, как и для десятичных чисел он равен 0, и нужно приписать к остатку (снести) очередной разряд делимого.
Рассмотрим последовательность 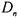 всех двоичных наборов длины
всех двоичных наборов длины
п в лексикографическом порядке. Если их прочитать как двоичные числа, игнорируя начальные нули, то это будет начальный отрезок
натурального ряда от 0 до 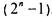 . Для любого
. Для любого 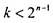 сумма k -го от
сумма k -го от
начала числа 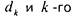 от конца
от конца 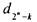 равна одному и тому же числу
равна одному и тому же числу
i 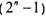 , которое в двоичной записи^состоит из п единиц. При вычитании
, которое в двоичной записи^состоит из п единиц. При вычитании
из двоичного числа  любого меньшего числа не требуется
любого меньшего числа не требуется
заимствования единиц из старших разрядов (подобно вычитанию из числа 99...9 в десятичной системе), и единице в вычитаемом соответствует ноль в разности, и наоборот, нулю в вычитаемом отвечает
единица в разности. Поэтому двоичные знаки числа 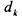 противоположны
противоположны
соответствующим знакам числа 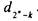 Другими словами, таблица
Другими словами, таблица 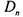
антисимметрична относительно своей середины.
Таблица 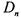 , строки которой суть наборы из 0 и 1 длины п, может быть построена по индуктивному правилу:
, строки которой суть наборы из 0 и 1 длины п, может быть построена по индуктивному правилу:
1) таблица 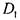 - это столбец из двух однозначных чисел 0 и 1;
- это столбец из двух однозначных чисел 0 и 1;
2) таблица  получается из двух экземпляров таблицы
получается из двух экземпляров таблицы  : к
: к
первому из них присоединяется слева столбец из 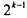 нулей, а ко
нулей, а ко
второму - столбец из 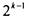 единиц. Расположенные одна под другой,
единиц. Расположенные одна под другой,
обе таблицы образуют таблицу 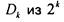 строк.
строк.







