23. 1. Методы вычисления определённых интегралов
Приближённое вычисление определённого интеграла основано  на геометрическом смысле интеграла и сводится к приближённому вычислению площади, ограниченной графиком подынтегральной функции f(x), прямыми x=a=x0, x=b=xn и осью OX (рис. 23.1).
на геометрическом смысле интеграла и сводится к приближённому вычислению площади, ограниченной графиком подынтегральной функции f(x), прямыми x=a=x0, x=b=xn и осью OX (рис. 23.1).
Интервал [a,b] делится на n равных частей длиной  .
.
 Тогда значениям xi=xi-1+h, i=1,2...,n, соответствуют значения yi=f(xi).
Тогда значениям xi=xi-1+h, i=1,2...,n, соответствуют значения yi=f(xi).
Метод прямоугольников. Согласно методу левых прямоугольников искомая площадь вычисляется как сумма площадей прямоугольников, основание которых равно h, а высота равна соответственно y0 для первого прямоугольника, y1 – для второго и т.д. вплоть до последнего с высотой yn-1. Тогда
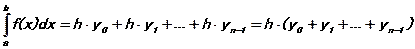 (23.1)
(23.1)
Для метода правых прямоугольников аналогично
 (23.2)
(23.2)
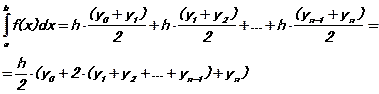
Метод трапеций. По методу трапеций определяется сумма площадей трапеций, основаниями которых являются ординаты y0, y1 и т.д., а высоты равны h.
 (23.3)
(23.3)
Погрешность метода оценивается как  , где М – максимальное значение второй производной f(x) на отрезке [a,b]. Используя это соотношение можно определить количество точек, на которое делится отрезок, исходя из заданной погрешности.
, где М – максимальное значение второй производной f(x) на отрезке [a,b]. Используя это соотношение можно определить количество точек, на которое делится отрезок, исходя из заданной погрешности.
 Значение интеграла, вычисленное по формуле трапеций, равно среднему арифметическому от значений интеграла, вычисленных по формулам левых и правых прямоугольников при том же разбиении.
Значение интеграла, вычисленное по формуле трапеций, равно среднему арифметическому от значений интеграла, вычисленных по формулам левых и правых прямоугольников при том же разбиении.
Рассмотрим алгоритм метода трапеций (рис. 23.2)
1. Ввод a, b, n.
2. Вычисление  ,
,
x=a+ h, s=0.
3. Вычисление s=s+f(x), x=x+h.
4. Если x>(b-h), то переход к пункту 5, иначе – переход к пункту 3.
5. Вычисление значения интеграла

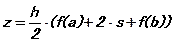
6. Вывод z.
Метод парабол (Симпсона). Согласно методу парабол интервал [a,b] делится на четное количество частей – 2n. Тогда
 , xi=xi-1+h, i=1,2,3…,2n
, xi=xi-1+h, i=1,2,3…,2n
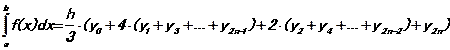 (23.4)
(23.4)
Алгоритм метода парабол.
1. Ввод a, b, n.
2. Вычисление 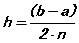 , x=a+2h, s1=0, s2=0, i=1.
, x=a+2h, s1=0, s2=0, i=1.
3. Вычисление s2=s2+f(x), x=x+h, s1=s1+f(x), x=x+h, i=i+1.
4. Если i<n-1, то переход к пункту 3, иначе – переход к следующему пункту.
5. Вычисление значения интеграла:

6. Вывод z.
Здесь s1=y3+y5+…+y2n-1, а s2=y2+y4+…+y2n-2.






