1.  :
:  ,
,  ,
, 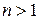 - нечетное.
- нечетное.
Уравнение  для любого
для любого 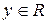 имеет единственное решение
имеет единственное решение  , поэтому функция
, поэтому функция  :
:  обратима и имеет обратную функцию
обратима и имеет обратную функцию 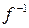 :
:  по правилу
по правилу 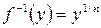 .
.
Обозначим аргумент обратной функции через  , получим
, получим
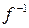 :
:  ,
,  .
.
Рассмотрим графики функций  и
и 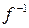 .
.

 .
.
График обратной функции 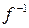 (рис. 6б) симметричен графику функции
(рис. 6б) симметричен графику функции  (рис. 6а) относительно биссектрисы первого и третьего координатных углов.
(рис. 6а) относительно биссектрисы первого и третьего координатных углов.





0  0
0 
Рис. 6а Рис. 6б
2. Отметим, что следующая функция не обратима:
 :
:  ,
,  ,
, 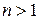 - четное.
- четное.



0 
Рис. 7
3.  :
:  ,
,  ,
, 
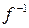 :
:  ,
,  .
.


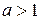


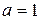
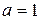

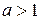


0  0
0 
Рис. 8а Рис. 8б
4.  :
:  ,
,  ,
, 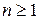 - нечетное
- нечетное
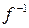 :
:  ,
,  .
.





0  0
0 
Рис. 9а Рис. 9б
5.  :
:  ,
,  ,
,  - четное. Эта функция не обратима.
- четное. Эта функция не обратима.



0 
Рис. 10
6.  :
:  ,
, 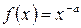 ,
, 
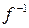 :
:  ,
,  .
.



1 1


0 1  0 1
0 1 
Рис. 11а Рис. 11б
7.  :
:  ,
, 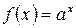 ,
,  ,
,  ,
,
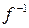 :
:  ,
,  .
.
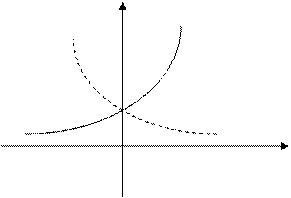




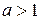

1 

0  0 1
0 1 
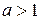
Рис. 12а
Рис. 12б
8.  :
:  ,
,  ,
,
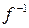 :
:  ,
,  .
.










 1
1 









 0 1
0 1  -1 0 1
-1 0 1
 -1
-1


Рис. 13а Рис. 13б
9.  :
:  ,
, 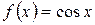 ,
,
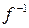 :
:  ,
,  .
.










 1
1 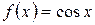




 0
0 

 -1 0 1
-1 0 1 
 -1
-1
Рис. 14а Рис. 14б
10.  :
:  ,
,  ,
,
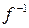 :
:  ,
,  .
.









 0
0  0
0

Рис. 15а Рис. 15б
11.  :
:  ,
,  ,
,
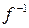 :
:  ,
,  .
.







 0
0 









