1. Аналитический способ задания функции
Если функция выражена при помощи формулы (аналитического выражения), позволяющего для значения 
вычислить (определить) значение функции (образ элемента 
) 
, то говорят, что она задана аналитически.
Пример. Рассмотрим функцию 
, определенную формулой 
и являющуюся отображением множества действительных чисел 
во множеством неотрицательных чисел 
, т.е.
, 
.
Заметим, что вполне возможно рассматривать отображение в , определенное соотношением 
, т.е.
, ;
Функции и 
различны, хотя и заданы одним и тем же аналитическим выражением, т.к. имеют различные области определения.
2. Табличный способ задания функции
Если 
- конечное множество, то функция 
может быть задана таблично:
| 
| 
| 
|
| 
| 
| 
|
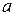
В верхней строке перечисляются элементы множества определения функции , в нижней указываются их образы. Например,
|
| |||
| -1 |
От аналитического способы задания функции всегда можно перейти к табличному, а обратный переход в общем случае сделать нельзя.
3. Задание графиком.
При графическом способе задания функции соответствие между переменными устанавливается с помощью графика.
Определение 1. Графиком функции 
: 
называется подмножество 
в декартовом произведении 
вида:
.
Нетрудно видеть, что функция однозначно определяет график и наоборот, по графику функция восстанавливается однозначно.
Примеры.
1. Функция : 
, 
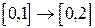задается графиком 
, 
.
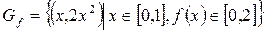0 1
Рис. 3
2. Рассмотрим функцию 
, 
, где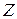 
- множество целых чисел, 
- целая часть, наибольшее целое число, не превосходящее .
На каждом промежутке 
, где 
функция постоянна и 
.
График данной функции изображен на рис. 4. Стрелки на графике означают, что точки на острие стрелки графику не принадлежат.
–2 –1 0 1 2 3
-1
-2
Рис. 4
4.Функция, заданная таблицей
|
| |||
|
|
Может быть задана графиком (рис.5)
0 1 2 3
Рис. 5
